苏科版数学九年级上册期中模拟试卷六（含答案）

这是一份苏科版数学九年级上册期中模拟试卷六（含答案），共9页。试卷主要包含了方程2x等内容，欢迎下载使用。
1．如图，AB为⊙O的直径，点C在⊙O上，∠A=40°，则∠B的度数为（ ）
A．20°B．40°C．50°D．60°
2．如图，AB是⊙O的直径，点C在⊙O上，若∠BOC=40°，则∠C的度数等于（ ）
A．20°B．40°C．60°D．80°
3．如图，△ABC的三边分别切⊙O于D，E，F，若∠A=50°，则∠DEF=（ ）
A．65°B．50°C．130°D．80°
4．方程2x（x﹣3）=5（x﹣3）的根是（ ）
A．x=B．x=3C．x1=，x2=3D．x1=﹣，x2=﹣3
5．如图，PA、PB是⊙O的切线，切点分别为A、B，点C在⊙O上，如果∠P=50°，那么∠ACB等于（ ）
A．40°B．50°C．65°D．130°
6．如图，已知⊙O的直径AB⊥弦CD于点E，下列结论中一定正确的是（ ）
A．AE=OEB．CE=DEC．OE=CED．∠AOC=60°
7．已知一个圆锥的底面半径为3cm，母线长为10cm，则这个圆锥的侧面积为（ ）
A．15πcm2B．30πcm2C．60πcm2D．3cm2
8．某商品原价500元，连续两次降价a%后售价为200元，下列所列方程正确的是（ ）
A．500（1+a%）2=200 B．500（1﹣a%）2=200
C．500（1﹣2a%）=200 D．500（1﹣a2%）=200
9．用公式法解﹣x2+3x=1时，先求出a、b、c的值，则a、b、c依次为（ ）
A．﹣1，3，﹣1B．1，﹣3，﹣1C．﹣1，﹣3，﹣1D．﹣1，3，1
10．如图，△ABC为⊙O的内接三角形，AB为⊙O的直径，点D在⊙O上，∠ADC=54°，则∠BAC的度数等于（ ）
A．36°B．44°C．46°D．54°
二.填空题
11．小华在解一元二次方程x2﹣4x=0时，只得出一个根是x=4，则被他漏掉的一个根x= ．
12．如图，⊙O是△ABC的外接圆，连接OA，OB，∠OBA=48°，则∠C的度数为 ．
13．如图，△ABC内接于⊙O，AH⊥BC于点H，若AC=24，AH=18，⊙O的半径OC=13，则AB= ．
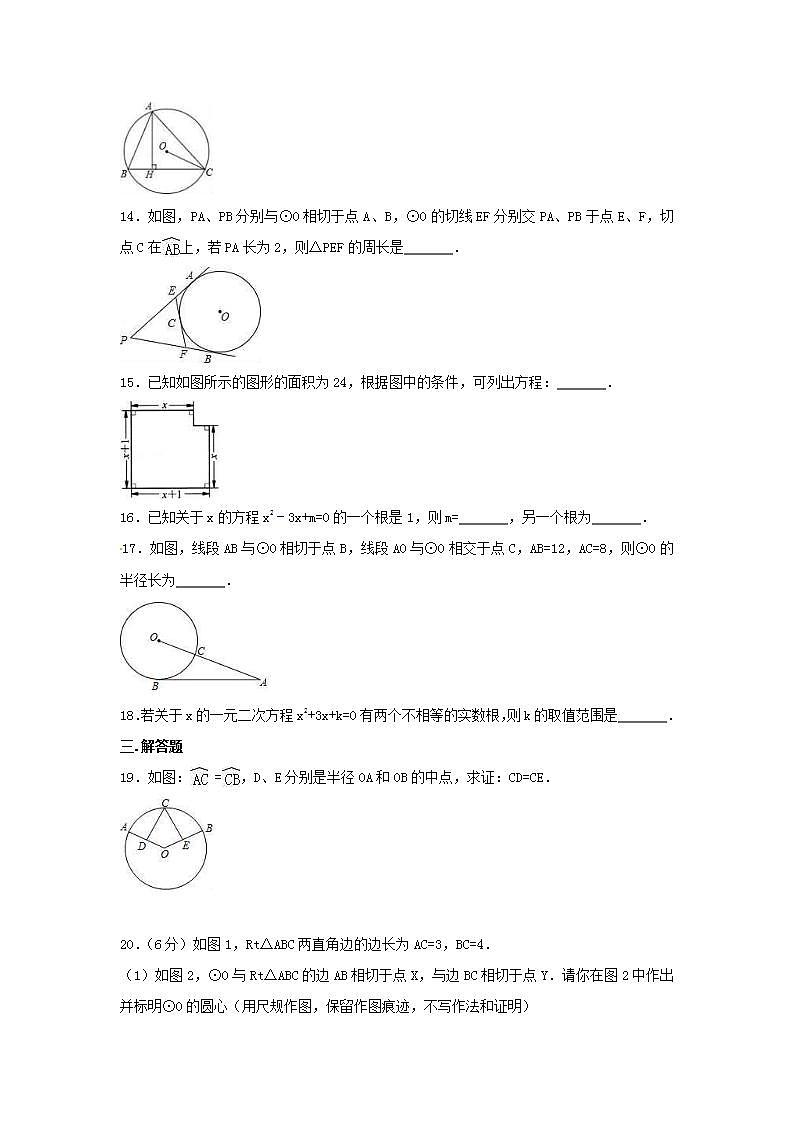
14．如图，PA、PB分别与⊙O相切于点A、B，⊙O的切线EF分别交PA、PB于点E、F，切点C在上，若PA长为2，则△PEF的周长是 ．
15．已知如图所示的图形的面积为24，根据图中的条件，可列出方程： ．
16．已知关于x的方程x2﹣3x+m=0的一个根是1，则m= ，另一个根为 ．
17．如图，线段AB与⊙O相切于点B，线段AO与⊙O相交于点C，AB=12，AC=8，则⊙O的半径长为 ．
18．若关于x的一元二次方程x2+3x+k=0有两个不相等的实数根，则k的取值范围是 ．
三.解答题
19．如图： =，D、E分别是半径OA和OB的中点，求证：CD=CE．
20．（6分）如图1，Rt△ABC两直角边的边长为AC=3，BC=4．
（1）如图2，⊙O与Rt△ABC的边AB相切于点X，与边BC相切于点Y．请你在图2中作出并标明⊙O的圆心（用尺规作图，保留作图痕迹，不写作法和证明）
（2）P是这个Rt△ABC上和其内部的动点，以P为圆心的⊙P与Rt△ABC的两条边相切．设⊙P的面积为S，你认为能否确定S的最大值？若能，请你求出S的最大值；若不能，请你说明不能确定S的最大值的理由．
21．已知：△ABC（如图），
（1）求作：作△ABC的内切圆⊙I．（要求：用尺规作图，保留作图痕迹，不写作法，不要求证明）．
（2）在题（1）已经作好的图中，若∠BAC=88°，求∠BIC的度数．
22．如图，点G．H分别是正六边形ABCDEF的边BC．CD上的点，且BG=CH，AG交BH于点P．
（1）求证：△ABG≌△BCH；
（2）求∠APH的度数．
23．岳一中初三某学生聆听了感恩励志主题演讲《不要让爱你的人失望》后，写了一份《改变，从现在开始》的倡议书在微信朋友圈传播，规则为：将倡议书发表在自己的朋友圈，再邀请n个好友转发倡议书，每个好友转发倡议书之后，又邀请n个互不相同的好友转发倡议书，依此类推，已知经过两轮传播后，共有421人参与了传播活动，求n的值．
24．在直径为10cm的圆柱形油槽内装入一些油后，截面如图，油面宽AB为6cm，当油面宽AB为8cm时，油上升了多少cm？

25．如图，点A是⊙O直径BD延长线上的一点，C在⊙O上，AC=BC，AD=CD
（1）求证：AC是⊙O的切线；
（2）若⊙O的半径为4，求△ABC的面积．

参考答案
1．故选：C．
2．故选：A．
3．故选：A．
4．故选：C．
5．故选：C．
6．故选：B．
7．故选：B．
8．故选：B．
9．故选：A．
10．故选：A．
11．0．
12．答案为：42°．
13．答案为：．
14．答案：4．
15．答案为：（x+1）2=25．
16．答案为：2，2．
17．答案为：5．
18．答案为：k＜．
19．证明：连接OC．
在⊙O中，∵=
∴∠AOC=∠BOC，
∵OA=OB，D、E分别是半径OA和OB的中点，
∴OD=OE，
∵OC=OC（公共边），
∴△COD≌△COE（SAS），
∴CD=CE（全等三角形的对应边相等）．
20．解：（1）由∠B得角平分线、平角∠BXA的平分线、平角∠BYC的角平分线中的任意两条得交点即为所求圆的圆心O；
（2）若⊙P与△ABC的BA、BC两条边相切，且面积最大，则点P为∠ABC的角平分线与AC边的交点，
作PH⊥AB于H，
∵Rt△ABC两直角边的边长为AC=3，BC=4，
∴AB=5，
则BH=BC=4，∴AH=1，
∵∠A=∠A，∠PHA=∠BCA，
∴△APH∽△ABC，
∴==，
∴PH=AH，
在Rt△APH中，PH=AH=，即R1=，
同理，⊙P与△ABC的CA、AC两条边相切，R2=，
若⊙P与△ABC的CA、BC两条边相切，R3=，
故R3＞R2＞R1，符合要求⊙P的最大面积为：．
21．解：（1）如图，⊙I为所作；
（2）∵⊙I为△ABC的内切圆，
∴BI平分∠ABC，CI平分∠ACB，
∴∠IBC=∠ABC，∠ICB=∠ACB，
∴∠IBC+∠ICB=（∠ABC+∠ACB）=（180°﹣∠BAC）=（180°﹣88°）=46°，
∴∠BIC=180°﹣∠IBC﹣∠ICB=180°﹣（∠IBC+∠ICB）=180°﹣46°=134°．
22．（1）证明：∵在正六边形ABCDEF中，
AB=BC，∠ABC=∠C=120°，
在△ABG与△BCH中，
∴△ABG≌△BCH；
（2）由（1）知：△ABG≌△BCH，
∴∠BAG=∠HBC，
∴∠BPG=∠ABG=120°，
∴∠APH=∠BPG=120°．
23．解：由题意，得n+n2+1=421，
解得：n1=﹣21（舍去），n2=20．
故所求n的值是20．
24．解：连接AO，过点O作OC⊥AB于点C，如图所示．
∵OC⊥AB于C，且AB为弦，
∴AC=AB．
当AB=6cm时，在Rt△OAC中，OA==5cm，AC=3cm，
∴OC==4cm；
当AB=8cm时，在Rt△OAC中，OA==5cm，AC=4cm，
∴OC==3cm．
∴4cm﹣3cm=1cm．
答：油上升了1cm．
25．解：（1）证明：如图，连接OC．
∵AC=BC，AD=CD，OB=OC，
∴∠A=∠B=∠1=∠2．
又∵BD是直径，
∴∠BCD=90°，
∵∠ACO=∠DCO+∠2，
∴∠ACO=∠DCO+∠1=∠BCD，
∴∠ACO=90°，即AC⊥OC，
又C在⊙O上，
∴AC是⊙O的切线；
（2）解：由题意可得△DCO是等腰三角形，
∵∠CDO=∠A+∠2，∠DOC=∠B+∠1，
∴∠CDO=∠DOC，即△DCO是等边三角形．
∴∠A=∠B=∠1=∠2=30°，CD=AD=OD=4，
在直角△BCD中，BC==4．
作CE⊥AB于点E．在直角△BEC中，∠B=30°，
∴CE=BC=2，
∴S△ABC=AB•CE=×12×2=12．