双曲线PPT课件免费下载

人教版（中职）高中数学拓展模块课文《双曲线》,完整版PPT课件免费下载，优秀PPT背景图搭配，精美的免费ppt模板。轻松备课，欢迎免费下载使用。
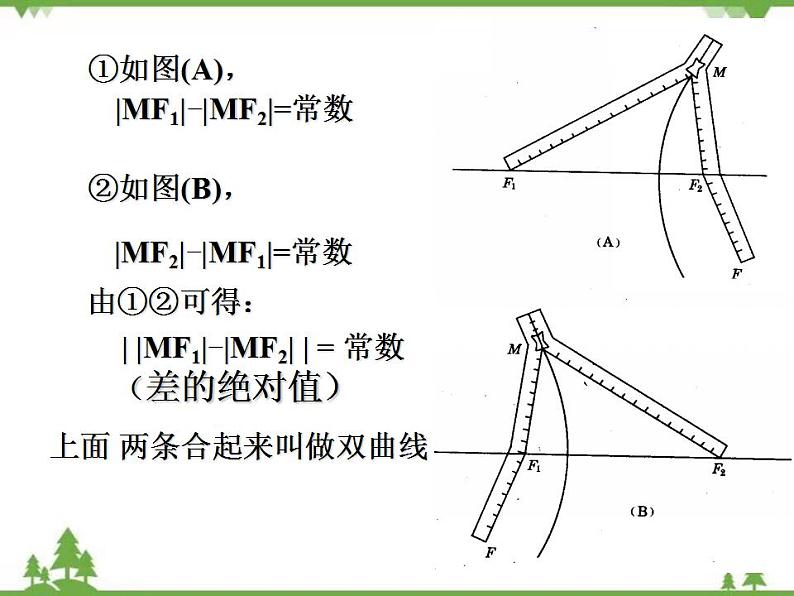
一、【课程主要内容】|MF1|+|MF2|=2a( 2a>|F1F2|>0) |MF1|-|MF2|=常数
上面 两条合起来叫做双曲线
| |MF1|-|MF2| | = 常数 （差的绝对值）
|MF2|-|MF1|=常数
双曲线在生活中 ☆.☆
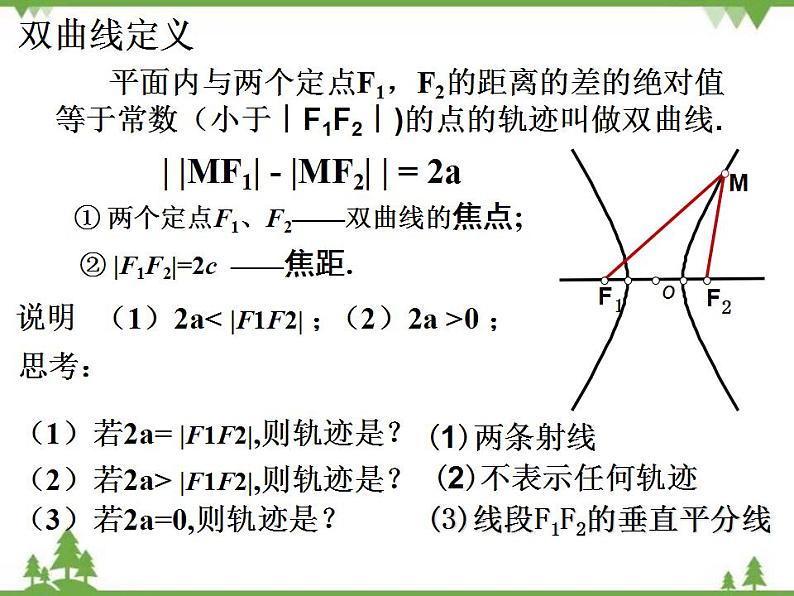
① 两个定点F1、F2——双曲线的焦点;
② |F1F2|=2c ——焦距.
（1）2a< |F1F2| ；
平面内与两个定点F1，F2的距离的差的绝对值等于常数（小于︱F1F2︱)的点的轨迹叫做双曲线.
（1）若2a= |F1F2|,则轨迹是？
（2）若2a> |F1F2|,则轨迹是？
（3）若2a=0,则轨迹是？
| |MF1| - |MF2| | = 2a
(3)线段F1F2的垂直平分线
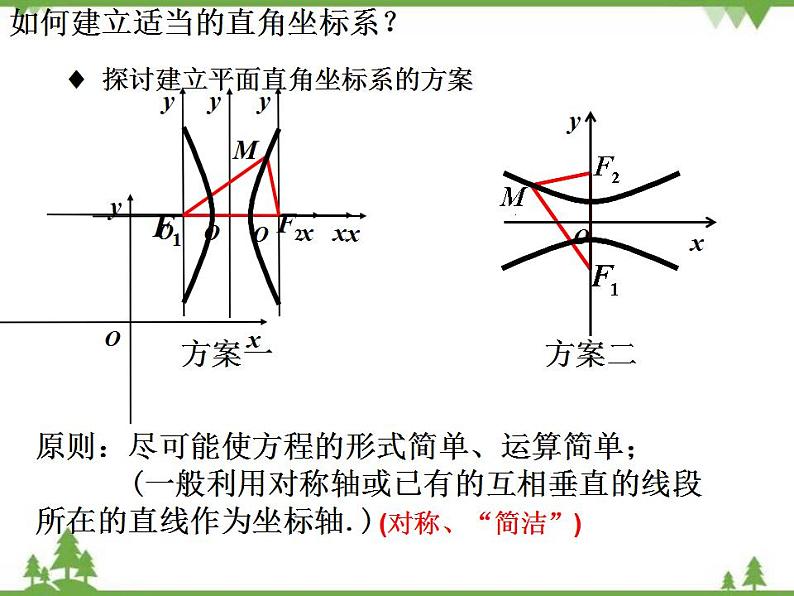
如何建立适当的直角坐标系？
原则：尽可能使方程的形式简单、运算简单； (一般利用对称轴或已有的互相垂直的线段所在的直线作为坐标轴.)二、【课堂讨论】♦ 探讨建立平面直角坐标系的方案
以F1,F2所在的直线为x轴，线段F1F2的中点为原点建立直角坐标系
设M（x , y）,则F1(-c,0),F2(c,0)
|MF1| - |MF2|=±2a
此即为焦点在x轴上的双曲线的标准方程
若建系时,焦点在y轴上呢?
2、双曲线的标准方程与椭圆的标准方程有何区别与联系?
1、如何判断双曲线的焦点在哪个轴上？
| |MF1|-|MF2| | =2a（０ < 2a<|F1F2|）
F ( ±c, 0) F(0, ± c)
a>0，b>0，但a不一定大于b，c2=a2+b2
a>b>0，a2=b2+c2
双曲线与椭圆之间的区别与联系
||MF1|－|MF2||=2a
|MF1|+|MF2|=2a
2. y2-2x2=1的焦点为 、焦距是 .
3.方程(2+)x2+(1+)y2=1表示双曲线的充要条件 是 .
方程表示的曲线是双曲线
方程表示的曲线是双曲线的右支
方程表示的曲线是x轴上分别以F1和F2为端点，指向x轴的负半轴和正半轴的两条射线。三、【典例剖析】利用双曲线的定义求轨迹问题 动圆M与圆C1：(x＋3)2＋y2＝9外切，且与圆C2：(x－3)2＋y2＝1内切，求动圆圆心M的轨迹方程．
【名师点评】 利用定义法求双曲线的标准方程，首先找出两个定点(即双曲线的两个焦点)；然后再根据条件寻找动点到两个定点的距离的差(或差的绝对值)是否为常数，这样确定c和a的值，再由c2＝a2＋b2求b2，进而求双曲线的方程．
使A、B两点在x轴上，并且点O与线段AB的中点重合
解: 由声速及在A地听到炮弹爆炸声比在B地晚2s,可知A地与爆炸点的距离比B地与爆炸点的距离远680m.因为|AB|>680m,所以爆炸点的轨迹是以A、B为焦点的双曲线在靠近B处的一支上.
例3.已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.
如图所示，建立直角坐标系xOy,
设爆炸点P的坐标为(x,y)，则
即 2a=680，a=340
因此炮弹爆炸点的轨迹方程为
答:再增设一个观测点C，利用B、C（或A、C）两处测得的爆炸声的时间差，可以求出另一个双曲线的方程，解这两个方程组成的方程组，就能确定爆炸点的准确位置.这是双曲线的一个重要应用.
【名师点评】 双曲线的定义是解决与双曲线有关的问题的主要依据，在应用时，一是注意条件||PF1|－|PF2||＝2a(0<2a<|F1F2|)的使用，二是注意与三角形知识相结合，经常利用正、余弦定理，同时要注意整体运算思想的应用．三、【课堂小结】1．对双曲线定义的理解双曲线定义中||PF1|－|PF2||＝2a(2a<|F1F2|)，不要漏了绝对值符号，当2a＝|F1F2|时表示两条射线．解题时，也要注意“绝对值”这一个条件，若去掉定义中的绝对值则轨迹仅表示双曲线的一支．
2．双曲线方程的求法求双曲线的标准方程包括“定位”和“定量”．“定位”是指除了中心在原点之外，判断焦点在哪个坐标轴上，以便使方程的右边为1时，确定方程的左边哪一项为正，哪一项为负，“定量”是指确定a2，b2的值，即根据条件列出关于a2和b2的方程组，解得a2和b2的具体数值后，再按位置特征写出标准方程．
易错警示 双曲线定义运用中的误区
【常见错误】 (1)利用双曲线定义||PF1|－|PF2||＝8求|PF2|时，易忽略绝对值号，而错选A.(2)根据双曲线的定义可得到答案C，但由于双曲线上的点到双曲线焦点的最小距离是c－a＝6－4＝2，而|PF2|＝1＜2，不合题意，所以应该舍去，造成错误的原因是忽略双曲线的相关性质，没有检验|PF1|＋|PF2|＝10＜|F1F2|造成的．
【解析】 双曲线的实轴长为8，由双曲线的定义得||PF1|－|PF2||＝8，所以|9－|PF2||＝8，所以|PF2|＝1或17.因为|F1F2|＝12，当|PF2|＝1时，|PF1|＋|PF2|＝10＜|F1F2|，不符合公理“两点之间线段最短”，应舍去．所以|PF2|＝17.【答案】 B
【失误防范】 运用双曲线的定义解决相关问题时，(1)不能忽略“绝对值”号，以免造成漏解，(2)求出解后，要注意检验根的合理性，以免出现增根．