初中数学人教版九年级下册第二十七章 相似综合与测试课时练习

这是一份初中数学人教版九年级下册第二十七章 相似综合与测试课时练习，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.观察下列每组图形，相似图形是（ ）
2.如果两个相似三角形对应边中线之比是1∶4，那么它们的对应高之比是（ ）
A.1∶2 B.1∶4 C.1∶8 D.1∶16
3.已知△ABC∽△DEF，且AB∶DE=1∶2，则△ABC的面积与△DEF的面积之比为（ ）
A.1∶2 B.1∶4 C.2∶1 D.4∶1
4.如图，l1∥l2∥l3，直线a、b与l1、l2、l3分别交于点A、B、C和点D、E、F.若eq \f(AB,BC)=eq \f(2,3)，DE=4，则EF的长是（ ）
A.eq \f(8,3) B.eq \f(20,3) C.6 D.10
5.如图，在直角坐标系中，有两点A(6，3)，B(6，0)，以原点O为位似中心，相似比为eq \f(1,3)，在第一象限内把线段AB缩小后得到CD，则C的坐标为（ ）
A.(2，1) B.(2，0) C.(3，3) D.(3，1)
6.如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（ ）
A.∠ABP=∠C B.∠APB=∠ABC C.eq \f(AP,AB)=eq \f(AB,AC) D.eq \f(AB,BP)=eq \f(AC,CB)
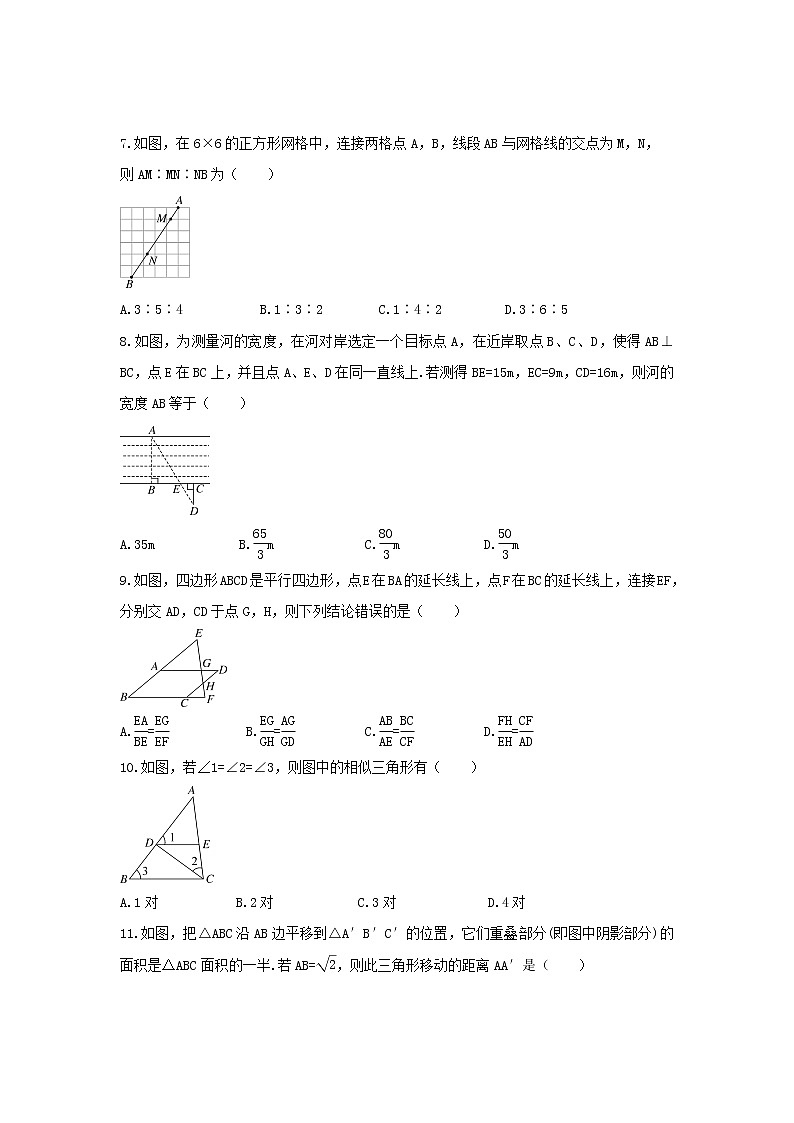
7.如图，在6×6的正方形网格中，连接两格点A，B，线段AB与网格线的交点为M，N，
则AM∶MN∶NB为（ ）
A.3∶5∶4 B.1∶3∶2 C.1∶4∶2 D.3∶6∶5
8.如图，为测量河的宽度，在河对岸选定一个目标点A，在近岸取点B、C、D，使得AB⊥BC，点E在BC上，并且点A、E、D在同一直线上.若测得BE=15m，EC=9m，CD=16m，则河的宽度AB等于（ ）
A.35m B.eq \f(65,3)m C.eq \f(80,3)m D.eq \f(50,3)m
9.如图，四边形ABCD是平行四边形，点E在BA的延长线上，点F在BC的延长线上，连接EF，分别交AD，CD于点G，H，则下列结论错误的是（ ）
A.eq \f(EA,BE)=eq \f(EG,EF) B.eq \f(EG,GH)=eq \f(AG,GD) C.eq \f(AB,AE)=eq \f(BC,CF) D.eq \f(FH,EH)=eq \f(CF,AD)
10.如图，若∠1=∠2=∠3，则图中的相似三角形有（ ）
A.1对 B.2对 C.3对 D.4对
11.如图，把△ABC沿AB边平移到△A′B′C′的位置，它们重叠部分(即图中阴影部分)的面积是△ABC面积的一半.若AB=eq \r(2)，则此三角形移动的距离AA′是（ ）
A.eq \r(2)－1 B.eq \f(\r(2),2) C.1 D.eq \f(1,2)
12.如图，在矩形ABCD中，E是AD边的中点，BE⊥AC于点F，连接DF.
分析下列四个结论：①△AEF∽△CAB；②CF=2AF；③DF=DC；④S四边形CDEF=eq \f(5,2)S△ABF.
其中正确的结论有（ ）
A.4个 B.3个 C.2个 D.1个
二、填空题
13.在比例尺为1∶4000 000的地图上，两城市间的图上距离为3cm，则这两城市间的实际距离为 km.
14.若实数a、b、c满足eq \f(b＋c,a)=eq \f(a＋c,b)=eq \f(a＋b,c)=k，则k= .
15.如图，身高为1.7m的小明AB站在河的一岸，利用树的倒影去测量河对岸一棵树CD的高度，CD在水中的倒影为C′D，A、E、C′在一条线上.已知河BD的宽度为12m，BE=3m，则树CD的高为 .
16.如图，正方形OABC与正方形ODEF是位似图形，点O为位似中心，相似比为1∶eq \r(3)，点E的坐标为(eq \r(3)，eq \r(3))，则点A的坐标是 .
17.如图，在Rt△ABC中，AB=BC，∠B=90°，AC=10eq \r(2).四边形BDEF是△ABC的内接正方形(点D、E、F在三角形的边上)，则此正方形的面积是 .
18.如图，菱形ABCD的边长为1，直线l过点C，交AB的延长线于M，交AD的延长线于N，则eq \f(1,AM)＋eq \f(1,AN)= .
三、解答题
19.如图，在△ABC中，DE∥BC，DE=2，BC=3.求eq \f(AE,AC)的值.
20.如图，已知在四边形ABCD中，∠ADB=∠ACB，延长AD，BC相交于点E.
求证：AC·DE=BD·CE.
21.如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC(顶点是网格线的交点).
(1)将△ABC向上平移3个单位得到△A1B1C1，请画出△A1B1C1；
(2)请画一个格点△A2B2C2，使△A2B2C2∽△ABC，且相似比不为1.
22.如图，在△ABC中，D是AB上一点，且∠ACD=∠B，已知AD=8cm，BD=4cm，求AC的长.
23.如图，已知在梯形ABCD中，AD∥BC，AB⊥BC，∠AEB=∠ADC.
(1)求证：△ADE∽△DBC；
(2)连接EC，若CD2=AD·BC，求证：∠DCE=∠ADB.
24.一天晚上，李明和张龙利用灯光下的影子来测量一路灯D的高度.如图，当李明走到点A处时，张龙测得李明直立身高AM与其影子长AE正好相等，接着李明沿AC方向继续向前走，走到点B处时，李明直立时身高BN的影子恰好是线段AB，并测得AB=1.25m.已知李明直立时的身高为1.75m，求路灯CD的高.
25.如图，△ABC中，∠ACB=90°，D为AB上一点，以CD为直径的⊙O交BC于点E，连接AE交CD于点P，交⊙O于点F，连接DF，∠CAE=∠ADF.
(1)判断AB与⊙O的位置关系，并说明理由；
(2)若PF∶PC=1∶2，AF=5，求CP的长.
26.如图，矩形OABC的顶点A、C分别在x轴和y轴上，点B的坐标为(2，3)，双曲线y=eq \f(k,x)(x>0)的图象经过BC上的点D，与AB交于点E，连接DE，若E是AB的中点.
(1)求点D的坐标；
(2)点F是OC边上一点，若△FBC和△DEB相似，求点F的坐标.
答案
1.D 2.B 3.B 4.C 5.A 6.D 7.B 8.C 9.C
10.D 11.A
12.A 解析：过D作DM∥BE交AC于点N，交BC于点M.∵四边形ABCD是矩形，∴AD∥BC，∠ABC=90°，AD=BC，∴∠EAC=∠ACB.∵BE⊥AC于点F，∴∠AFE=∠ABC=90°，∴△AEF∽△CAB，故①正确；∵AD∥BC，∴△AEF∽△CBF，∴eq \f(AE,BC)=eq \f(AF,CF).∵AE=eq \f(1,2)AD=eq \f(1,2)BC，∴eq \f(AF,CF)=eq \f(1,2)，∴CF=2AF，故②正确；∵DE∥BM，BE∥DM，∴四边形BMDE是平行四边形，∴BM=DE=eq \f(1,2)BC，∴BM=CM，∴CN=NF.∵BE⊥AC于点F，DM∥BE，∴DN⊥CF，∴DN垂直平分CF，∴DF=DC，故③正确；∵△AEF∽△CBF，eq \f(EF,BF)=eq \f(AE,BC)=eq \f(1,2)，∴S△AEF=eq \f(1,2)S△ABF，∴S△AEF=eq \f(1,3)S△ABE=eq \f(1,12)S矩形ABCD.又∵S四边形CDEF=S△ACD－S△AEF=eq \f(1,2)S矩形ABCD－eq \f(1,12)S矩形ABCD=eq \f(5,12)S矩形ABCD=5S△AEF=eq \f(5,2)S△ABF，故④正确.故选A.
13.120 14.－1或2 16.(0，1) 17.25 18.1
19.解：∵DE∥BC，∴△ADE∽△ABC，(5分)∴eq \f(AE,AC)=eq \f(DE,BC)=eq \f(2,3).(10分)
20.证明：∵∠ADB=∠ACB，∴∠EDB=∠ECA.(3分)又∵∠E=∠E，∴△ECA∽△EDB，(7分)∴eq \f(AC,BD)=eq \f(CE,DE)，即AC·DE=BD·CE.(10分)
21.解：(1)作出△A1B1C1，如图所示；(5分)
(2)作出△A2B2C2，如图所示(本题是开放题，答案不唯一，只要作出的△A2B2C2满足条件即可)(10分).
22.解：∵在△ACD和△ABC中，eq \b\lc\{(\a\vs4\al\c1(∠A＝∠A，,∠ACD＝∠B，))∴△ACD∽△ABC，∴eq \f(AD,AC)=eq \f(AC,AB).(5分)∵AD=8cm，BD=4cm，∴AB=12cm，∴eq \f(8,AC)=eq \f(AC,12)，(8分)∴AC=4eq \r(6)cm.(10分)
23.证明：(1)∵AD∥BC，∴∠ADE=∠DBC，∠ADC＋∠BCD=180°.(2分)∵∠AEB=∠ADC，∠AEB＋∠AED=180°，∴∠AED=∠BCD，(5分)∴△ADE∽△DBC；(6分)
(2)由(1)可知△ADE∽△DBC，∴eq \f(AD,DB)=eq \f(DE,BC)，∴DB·DE=AD·BC.(7分)∵CD2=AD·BC，∴CD2=DB·DE，∴eq \f(CD,DB)=eq \f(DE,CD).(8分)又∵∠CDE=∠BDC，∴△CDE∽△BDC，∴∠DCE=∠DBC.(10分)又∵∠ADB=∠DBC，∴∠DCE=∠ADB.(12分)
24.解：设CD=xm.∵AE=AM，AM⊥EC，∴∠E=45°，∴EC=CD=xm，AC=(x－1.75)m.(2分)∵CD⊥EC，BN⊥EC，BN∥CD，∴△ABN∽△ACD，(7分)∴eq \f(BN,CD)=eq \f(AB,AC)，即eq \f(1.75,x)=eq \f(1.25,x－1.75)，解得x=6.125.
答：路灯CD的高为6.125m.
25.解：(1)AB是⊙O的切线.(1分)理由如下：∵∠ACB=90°，∴∠CAE＋∠CEA=90°.(3分)又∵∠CEA=∠CDF，∠CAE=∠ADF，∴∠ADF＋∠CDF=90°，∴∠ADC=90°，∴CD⊥AD，∴AB是⊙O的切线；(6分)
(2)∵∠CPF=∠APC，连接DE、CF，如图.∵CD是直径，∴∠DEC=90°.∵∠ACB=90°，∴∠DEC＋∠ACE=180°，∴DE∥AC，∴∠DEA=∠CAE，又∵∠PCF=∠DEA，∴∠PCF=∠PAC.∴△PCF∽△PAC，∴eq \f(PC,PA)=eq \f(PF,PC)，∴PC2=PF·PA.(9分)设PF=a，∵PF∶PC=1∶2，则PC=2a，PA=a＋5，∴4a2=a(a＋5)，∴a=eq \f(5,3)或a=0(舍去)，∴PC=2a=eq \f(10,3).(12分)
26.解：(1)∵四边形OABC为矩形，∴AB⊥x轴.∵E为AB的中点，点B的坐标为(2，3)，∴点E的坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(2，\f(3,2))).∵点E在反比例函数y=eq \f(k,x)的图象上，∴k=3，∴反比例函数的解析式为y=eq \f(3,x).(4分)∵四边形OABC为矩形，∴点D与点B的纵坐标相同，将y=3代入y=eq \f(3,x)可得x=1，∴点D的坐标为(1，3)；(6分)
(2)由(1)可得BC=2，CD=1，∴BD=BC－CD=1.∵E为AB的中点，∴BE=eq \f(3,2).(8分)若△FBC∽△DEB，则eq \f(CB,BE)=eq \f(CF,BD)，即eq \f(2,\f(3,2))=eq \f(CF,1)，∴CF=eq \f(4,3)，∴OF=CO－CF=3－eq \f(4,3)=eq \f(5,3)，∴点F的坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(5,3)))；(11分)若△FBC∽△EDB，则eq \f(BC,DB)=eq \f(CF,BE)，即eq \f(2,1)=eq \f(CF,\f(3,2))，∴CF=3，此时点F和点O重合.(13分)综上所述，点F的坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(5,3)))或(0，0).(14分)