江苏省连云港市海州区新海中学2021-2022学年九年级上学期第一次月考数学【试卷+答案】

这是一份江苏省连云港市海州区新海中学2021-2022学年九年级上学期第一次月考数学【试卷+答案】，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．下列方程中，是关于x的一元二次方程的是（ ）
A．x+1x=2B．2x2﹣x＝1C．3x3＝1D．xy＝4
2．若x＝﹣1是一元二次方程ax2+bx+c＝0的根，则下列式子成立的是（ ）
A．a+b+c＝0B．a﹣b+c＝0C．a+b﹣c＝0D．﹣a+b+c＝0
3．某校为落实“光盘行动”，对每天的剩饭菜进行称重，第一周的剩余量为20kg，第三周为9.8kg，设每周剩余量的平均减少率为x，则可列方程（ ）
A．20（1﹣x）2＝9.8B．20（1+x）2＝9.8
C．20（1﹣2x）＝9.8D．20（1+2x）＝9.8
4．已知△ABC中，AB＝BC，若以点B为圆心，以AB为半径作圆，则点C（ ）
A．在⊙B上B．在⊙B外C．在⊙B内D．不能确定
5．如图，OA为⊙O的半径，弦BC⊥OA于点P．若BC＝8，AP＝2，则⊙O的直径长为（ ）
A．6B．5C．10D．217
6．已知任意实数a、b满足等式x＝a2﹣6ab+9b2，y＝4a﹣12b﹣4，则x，y的大小关系是（ ）
A．x＝yB．x＞yC．x＜yD．x≥y
7．下列语句中，正确的有（ ）
①相等的圆心角所对的弧相等；
②等弦对等弧；
③长度相等的两条弧是等弧；
④经过圆心的每一条直线都是圆的对称轴；
⑤三角形的外心到三角形的三边距离相等．
A．1个B．2个C．3个D．4个
8．若m，n（m＜n）是关于x的一元二次方程（x﹣a）（x﹣b）﹣3＝0的两根，若a＜b，则m，n，a，b的大小关系是（ ）
A．m＜n＜a＜bB．a＜m＜n＜bC．a＜m＜b＜nD．m＜a＜b＜n
二、填空题（本大题共8小题，每小题3分，满分24分）
9．若关于x的方程xm2+1-x-2=0是一元二次方程，则m的值为 ．
10．在解一元二次方程x2+px+q＝0时，小明看错了系数p，解得方程的根为1和﹣3；小红看错了系数q，解得方程的根为4和﹣2，则p＝ ．
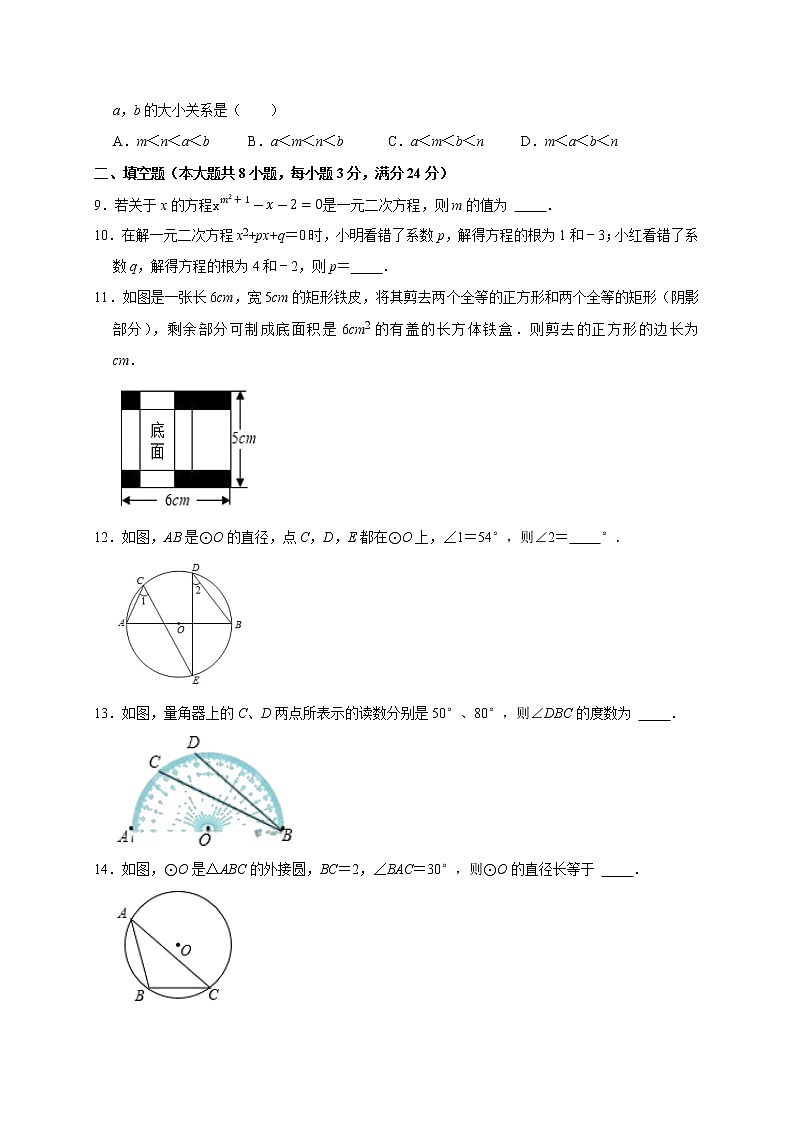
11．如图是一张长6cm，宽5cm的矩形铁皮，将其剪去两个全等的正方形和两个全等的矩形（阴影部分），剩余部分可制成底面积是6cm2的有盖的长方体铁盒．则剪去的正方形的边长为 cm．
12．如图，AB是⊙O的直径，点C，D，E都在⊙O上，∠1＝54°，则∠2＝ °．
13．如图，量角器上的C、D两点所表示的读数分别是50°、80°，则∠DBC的度数为 ．
14．如图，⊙O是△ABC的外接圆，BC＝2，∠BAC＝30°，则⊙O的直径长等于 ．
15．如图，在平面直角坐标系xOy中，点A，B，P的坐标分别为（1，0），（2，5），（4，2），若点C在第一象限内，且横坐标、纵坐标均为整数，点P是△ABC的外心，则符合条件的C点有 个．
16．如图，在△ABC中，AC=3，BC=43，∠ACB=60°，过点A作BC的平行线l，P为直线l上一动点，⊙O为△APC的外接圆，直线BP交⊙O于E点，则AE的最小值为 ．
三、解答题（本大题共10小题，共102分，把解答过程写在在题卡相应的位置上，解答时应写出必要的计算过程、推演步骤或文字说明.）
17．解方程：
（1）3x2﹣1＝4x；
（2）（x+4）2＝5（x+4）．
18．若关于x，y的二元一次方程组x+2y=7a-12x-y=-a+3的解x＞0，y＞0．
（1）求a的取值范围；
（2）若x是一个直角三角形的直角边长，y是其斜边长，此三角形另一条直角边的长为方程m2﹣8m+16＝0的解，求这个直角三角形的面积．
19．已知关于x的一元二次方程kx2+x﹣3＝0有两个不相等的实数根．
（1）求实数k的取值范围；
（2）设方程两个实数根分别为x1，x2，且满足（x1+x2）2+x1•x2＝4，求k的值．
20．2020年3月，新冠肺炎疫情在中国已经得到有效控制，但在全球却开始持续蔓延，这是对人类的考验，将对全球造成巨大影响．新冠肺炎具有人传人的特性，若一人携带病毒，未进行有效隔离，经过两轮传染后共有256人患新冠肺炎，求每轮传染中平均每个人传染了几个人？
21．阅读下列材料：
平面上两点P1（x1，y1），P2（x2，y2）之间的距离表示为|P1P2|=(x1-x2)2+(y1-y2)2，称为平面内两点间的距离公式，根据该公式，如图，设P（x，y）是圆心坐标为C（a，b）、半径为r的圆上任意一点，则点P适合的条件可表示为(x-a)2+(y-b)2=r，变形可得：（x﹣a）2+（y﹣b）2＝r2，我们称其为圆心为C（a，b），半径为r的圆的标准方程．
例如：由圆的标准方程（x﹣1）2+（y﹣2）2＝25可得它的圆心为（1，2），半径为5．根据上述材料，结合你所学的知识，完成下列各题．
（1）圆心为C（3，4），半径为2的圆的标准方程为： ；
（2）若已知⊙C的标准方程为：（x﹣2）2+y2＝22，圆心为C，请判断点A（3，﹣1）与⊙C的位置关系．
22．如图所示，AB是⊙O的弦，OD⊥AB，垂足为C，交⊙O于点D，点E在⊙O上．
（1）若∠AOD＝56°，求∠DEB的度数；
（2）若DC＝2，OA＝10，求AB的长．
23．第十四届全运会将于2021年9月15日至9月27日在陕西举行，铁一中分校学生为了迎接这一盛事，亲自设计并生产一种“铁一迎全运”的纪念徽章，并将这种纪念徽章在网上进行销售．平均每天可售出30枚，每枚盈利50元．为了扩大销售，增加盈利，现采取了降价措施，在每枚盈利不少于32元的前提下，销售一段时间后，发现销售单价每降低1元，平均每天可多售出2枚，若每枚商品降价a（a＞0）元．
（1）用含a的代数式表示平均每天销售的数量，并写出a的取值范围；
（2）若该网店每天销售利润为2100元时，求a的值．
24．把两个等腰直角△ABC和△ADE按如图1所示的位置摆放，将△ADE绕点A按逆时针方向旋转，如图2，连接BD，EC，设旋转角为α（0°＜α＜360°）．
（1）当DE⊥AC时，AD与BC的位置关系是 ，AE与BC的位置关系是 ．
（2）如图2，当点D在线段BE上时，求∠BEC的度数．
（3）若△ABD的外心在边BD上，直接写出旋转角α的值．
25．如图，△ABC中，AB＝AC，⊙O是△ABC的外接圆，BO的延长线交边AC于点D．
（1）求证：∠BAC＝2∠ABD；
（2）当△BCD是等腰三角形时，求∠BCD的大小．
26．如图，点A和动点P在直线上，点P关于点A的对称点为Q，以AQ为边作Rt△ABQ，使∠BAQ＝90°，AQ：AB＝3：4，作出△ABQ的外接圆O．点C在点P右侧且PC＝4，过点C作直线m⊥l，过点O作OD⊥m于点D，交AB右侧的圆弧于点E．在射线CD上取点F，使DF=32CD，以DE，DF为邻边作矩形DEGF．设AQ＝3x．
（1）用关于x的代数式表示BQ＝ ，DF＝ ；
（2）当点P在点A右侧时，若矩形DEGF的面积等于90，求AP的长；
（3）当点P在点A右侧时，作直线BG交⊙O于点N，若BN的弦心距为1，求AP的长．