2020-2021学年甘肃省天水高二（下）4月周考数学（文）试卷人教A版

这是一份2020-2021学年甘肃省天水高二（下）4月周考数学（文）试卷人教A版，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1. 已知复数z=1+2i2+i，则|z|=( )
A.5B.25C.5D.1

2. 命题“若x=0，则xy=0”的逆否命题是（ ）
A.若x=0，则xy≠0B.若xy≠0，则x≠0
C.若xy≠0，则x=0D.若x≠0，则xy≠0

3. 若复数(a2−3a+2)+(a−1)i是纯虚数，则实数a的值为( )
A.1或2B.2C.3D.4

4. 函数fx=x4−2x3的图像在点1,f1处的切线方程为( )
A.y=−2x−1B.y=−2x+1C.y=2x−3D.y=2x+1

5. 已知双曲线x2a2−y2b2=1(a>0,b>0)的一条渐近线与圆(x−4)2+y2=4相切，离心率为( )
A.2B.233C.3D.32

6. 某一组数据对应的线性回归方程为y=−0.76x+a，数据中心点为(5, 1)，则x=7.5的预报值是( )
A.0.9B.−0.9C.1D.−1

7. 函数y=x3−x2−x−1的单调递增区间为( )
A.−1,13B.−13,1
C.−∞,−1，13,+∞D.−∞,−13，1,+∞

8. 已知a为正实数，若函数fx=x3−3ax2+2a2的极小值为0，则a的值为( )
A.12B.1C.32D.2

9. 过曲线y=ex−x外一点e,−e作该曲线的切线l，则l在y轴上的截距为（ ）
A.−eeB.−ee+2C.−ee+1D.ee+2

10. 已知抛物线x2=4y的准线与双曲线x2a2−y2b2=1(a>0，b>0)的两条渐近线围成一个等腰直角三角形，则该双曲线的离心率是( )
A.2B.2C.5D.5
二、填空题

在平面直角坐标系xOy中，抛物线y2=−8x的焦点坐标为________．
三、解答题

设a为实数，函数fx=2x3−15x2+36x+a.
(1)求fx的极值；

(2)若函数y=fx的图像与x轴仅有一个交点，求a的取值范围．

已知F1，F2分别是双曲线C:x2a2−y2b2=1(a>0,b>0)的左、右焦点，点P是双曲线上一点，满足PF1⊥PF2且|PF1|=8，|PF2|=6．
(1)求双曲线C的标准方程；

(2)若直线l交双曲线于A，B两点，若AB的中点恰为点M(2, 6)，求直线l的方程．


科学家为研究对某病毒有效的疫苗，通过小鼠进行毒性和药效预实验．为了比较注射A，B两种疫苗后产生的抗体情况，选200只小鼠做实验，将这200只小鼠随机分成两组，每组100只，其中一组注射疫苗A，另一组注射疫苗B．下表1和表2分别是注射疫苗A和疫苗B后的实验结果．
表1：注射疫苗A后产生抗体参数的频率分布表
表2：注射疫苗B 后产生抗体参数的频率分布表

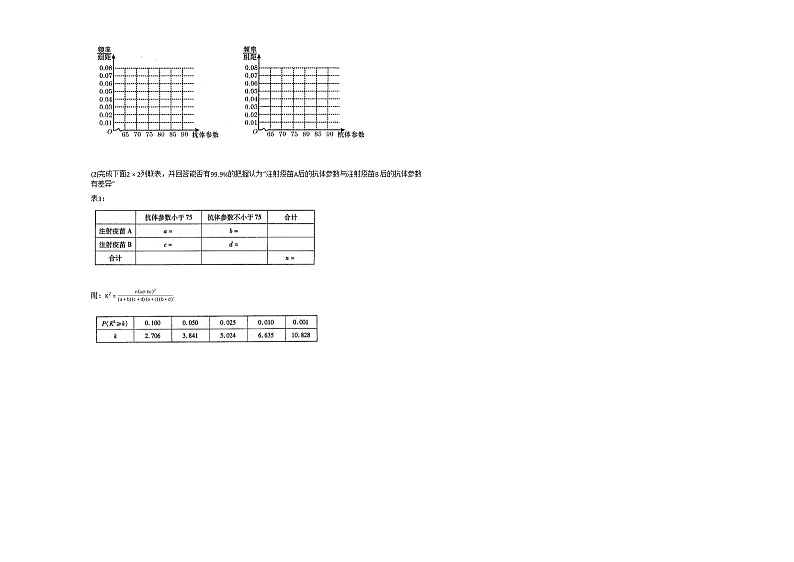
(1)完成下面频率分布直方图，并比较注射两种疫苗后抗体参数的中位数大小；

(2)完成下面2×2列联表，并回答能否有99.9%的把握认为“注射疫苗A后的抗体参数与注射疫苗B 后的抗体参数有差异”
表3：
附：K2=nad−bc2a+bc+da+cb+d.
参考答案与试题解析
2020-2021学年甘肃省天水市高二（下）4月周考数学（文）试卷
一、选择题
1.
【答案】
D
【考点】
复数的模
复数代数形式的乘除运算
【解析】

【解答】
解：因为z=1+2i2+i=(1+2i)(2−i)(2+i)(2−i)=45+35i，
所以|z|=1 .
故选D.
2.
【答案】
B
【考点】
四种命题的定义
【解析】
根据逆否命题的定义进行判断即可．
【解答】
解：命题若p，则q的逆否命题为：若¬q，则¬p，
即命题若x=0，则xy=0的逆否命题为：若xy≠0，则x≠0.
故选B．
3.
【答案】
B
【考点】
复数的基本概念
【解析】
注意到复数a+bi，a，b∈R为纯虚数的充要条件是a=0b≠0.
【解答】
解：因为(a2−3a+2)+(a−1)i是纯虚数，
所以a2−3a+2=0，a−1≠0，
解得a=2．
故选B．
4.
【答案】
B
【考点】
利用导数研究曲线上某点切线方程
【解析】
先求得原函数的导数，根据切点的横坐标，求出切线的斜率和切点的纵坐标，进而得到所求切线的方程．
【解答】
解：由题知：f′x=4x3−6x2．
则函数在点1,f(1)处的切线的斜率为：
k=f′1=−2，
∵ f1=−1．
∴ 切线方程为：y−−1=−2x−1．
化简得y=−2x+1.
故选B.
5.
【答案】
B
【考点】
双曲线的离心率
直线与圆的位置关系
双曲线的渐近线
【解析】
求出双曲线的渐近线方程，利用渐近线与圆相切，列出方程，然后求解双曲线的离心率即可．
【解答】
解：双曲线x2a2−y2b2=1(a>0,b>0)的一条渐近线y=bax与圆(x−4)2+y2=4相切，
可得：|4ba|1+(ba)2=2，解得a2=3b2，
从而a2=3(c2−a2)⇒4a2=3c2⇒2a=3c，
解得e=ca=233．
故选B.
6.
【答案】
B
【考点】
求解线性回归方程
【解析】
此题暂无解析
【解答】
解：由题意可得，1=−0.76×5+a，则a=4.8.
当x=7.5时，y=−0.76×7.5+4.8=−0.9.
故选B.
7.
【答案】
D
【考点】
利用导数研究函数的单调性
【解析】
先对函数进行求导，然后令导函数大于0求出x的范围即可．
【解答】
解：∵ y=x3−x2−x−1，
∴ y′=3x2−2x−1，
令y′>0，
即3x2−2x−1=3x+1x−1>0，
解得x1，
∴ 函数单调递增区间为−∞,−13，(1,+∞)．
故选D．
8.
【答案】
A
【考点】
利用导数研究函数的极值
【解析】
此题暂无解析
【解答】
解：由已知f′(x)=3x2−6ax=3x(x−2a)，
又a>0，
所以由f′x>0得x2a，
由f′x0)的两条渐近线关于y轴对称，
抛物线的准线与双曲线的渐近线组成等腰直角三角形，
所以双曲线的渐近线的斜率为±1，
得a=b，
所以c=2a，
所以e=ca=2．
故选A．
二、填空题
【答案】
−2,0
【考点】
抛物线的定义
【解析】

【解答】
解：∵ 抛物线的方程为y2=−8x，
∴ 2p=−8，
∴ p=−4，p2=−2．
∴ 抛物钱方程y2=−8x的焦点坐标为−2,0．
故答案为：−2,0．
三、解答题
【答案】
解：(1)f′x=6x2−30x+36=6x−2x−3，
令f′x=0，得x1=2，x2=3，
当x变化时f′x，fx的变化情况如下表：
∴ fx的极大值是f2=28+a，极小值是f3=27+a .
(2)结合(1)中fx的单调性，
当x→−∞时fx→−∞；当x→+∞时fx→+∞，
y=fx的图像与x轴仅有一个交点，则有f2=28+a0，
解得a−27 .
∴ a的取值范围是−∞,−28∪−27,+∞．
【考点】
利用导数研究函数的极值
利用导数研究与函数零点有关的问题
【解析】
此题暂无解析
【解答】
解：(1)f′x=6x2−30x+36=6x−2x−3，
令f′x=0，得x1=2，x2=3，
当x变化时f′x，fx的变化情况如下表：
∴ fx的极大值是f2=28+a，极小值是f3=27+a .
(2)结合(1)中fx的单调性，
当x→−∞时fx→−∞；当x→+∞时fx→+∞，
y=fx的图像与x轴仅有一个交点，则有f2=28+a0，
解得a−27 .
∴ a的取值范围是−∞,−28∪−27,+∞．
【答案】
解：(1)由题意得，2a=|PF1|−|PF2|=2，
所以a=1，
在三角形PF1F2中，|F1F2|2=|PF1|2+|PF2|2=100，
所以4c2=100，则c2=25=a2+b2，则b2=24，
故双曲线的标准方程为：x2−y224=1．
(2)设A(x1, y1)，B(x2, y2)，
有x12−y1224=1，x22−y2224=1，
则x12−x22=y12−y2224，
所以24=y12−y22x12−x22=y1−y2x1−x2⋅y1+y2x1+x2.
又kAB=y1−y2x1−x2，y1+y2x1+x2=62=3，
所以kAB⋅3=24，
可得kAB=8，
所以直线AB方程为：y−6=8(x−2)，
即y=8x−10，满足Δ>0，符合题意．
【考点】
双曲线的标准方程
直线与双曲线的位置关系
直线与双曲线结合的最值问题
【解析】
（1）利用双曲线的定义求出a＝1，在三角形PF1F2中，利用勾股定理求解c，然后求解双曲线方程．
（2）设A(x1, y1)，B(x2, y2)，利用点差法求解周长AB的向量，然后推出方程即可．
【解答】
解：(1)由题意得，2a=|PF1|−|PF2|=2，
所以a=1，
在三角形PF1F2中，|F1F2|2=|PF1|2+|PF2|2=100，
所以4c2=100，则c2=25=a2+b2，则b2=24，
故双曲线的标准方程为：x2−y224=1．
(2)设A(x1, y1)，B(x2, y2)，
有x12−y1224=1，x22−y2224=1，
则x12−x22=y12−y2224，
所以24=y12−y22x12−x22=y1−y2x1−x2⋅y1+y2x1+x2.
又kAB=y1−y2x1−x2，y1+y2x1+x2=62=3，
所以kAB⋅3=24，
可得kAB=8，
所以直线AB方程为：y−6=8(x−2)，
即y=8x−10，满足Δ>0，符合题意．
【答案】
解：(1)频率分布直方图完成如下：
可以看出注射疫苗A后的抗体参数的中位数在70至75之间，
而注射疫苗B后的抗体参数的中位数在75至80之间，
所以注射疫苗A后抗体参数的中位数小于注射疫苗B后抗体参数的中位数 .
(2)完成表3如下：
K2=200×(70×65−35×30)2100×100×105×95≈24.56，
由于K2>10.828，
所以有99.9%的把握认为“注射疫苗A后的抗体参数与注射疫苗B后的抗体参数有差异”．
【考点】
众数、中位数、平均数
频率分布直方图
独立性检验
【解析】


【解答】
解：(1)频率分布直方图完成如下：
可以看出注射疫苗A后的抗体参数的中位数在70至75之间，
而注射疫苗B后的抗体参数的中位数在75至80之间，
所以注射疫苗A后抗体参数的中位数小于注射疫苗B后抗体参数的中位数 .
(2)完成表3如下：
K2=200×(70×65−35×30)2100×100×105×95≈24.56，
由于K2>10.828，
所以有99.9%的把握认为“注射疫苗A后的抗体参数与注射疫苗B后的抗体参数有差异”．x
−∞,2
2
2,3
3
3,+∞
f′x
+
0
−
0
+
fx
↗
极大值
↘
极小值
↗
x
−∞,2
2
2,3
3
3,+∞
f′x
+
0
−
0
+
fx
↗
极大值
↘
极小值
↗