2021年吉林省长春市九年级上学期数学期中试卷含答案

这是一份2021年吉林省长春市九年级上学期数学期中试卷含答案，共15页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。
 九年级上学期数学期中试卷
一、单项选择题
1.等于〔  〕
A. 3                                          B. -3                                          C. ±3                                          D. 9
2.以下二次根式中，是最简二次根式的是〔  〕
A.                                      B.                                      C.                                      D. 
3.一元二次方程 的一次项系数和常数项分别是〔  〕
A. -3，-4                                  B. -3，4                                  C. 3，-4                                  D. 1，4
4.假设用配方法解方程 ，通常要在此方程两边同时加上一个“适当〞的数，那么下面变形恰当的是〔  〕
A.                             B. 
C.                                           D. 
5.假设 ，那么 等于〔  〕
A.                                           B.                                           C.                                           D. 3.
6.如图，比例规是伽利略创造的一种画图工具，使用它可以把线段按一定比例伸长或缩短，它是由长度相等的两脚 和 交叉构成的．如果把比例规的两脚合上，使螺丝钉固定在刻度3的地方〔即同时使 ， 〕，然后张开两脚，使A、B两个尖端分别在线段I的两个端点上．假设 ，那么 的长是〔  〕

A.                                     B.                                     C.                                     D. 
7.如图， ，直线 、 与这三条平行线分别交于点A、B、C和点D、E、F，假设 ， ， ，那么 的长是〔  〕

A. 4                                           B. 6                                           C. 8                                           D. 12
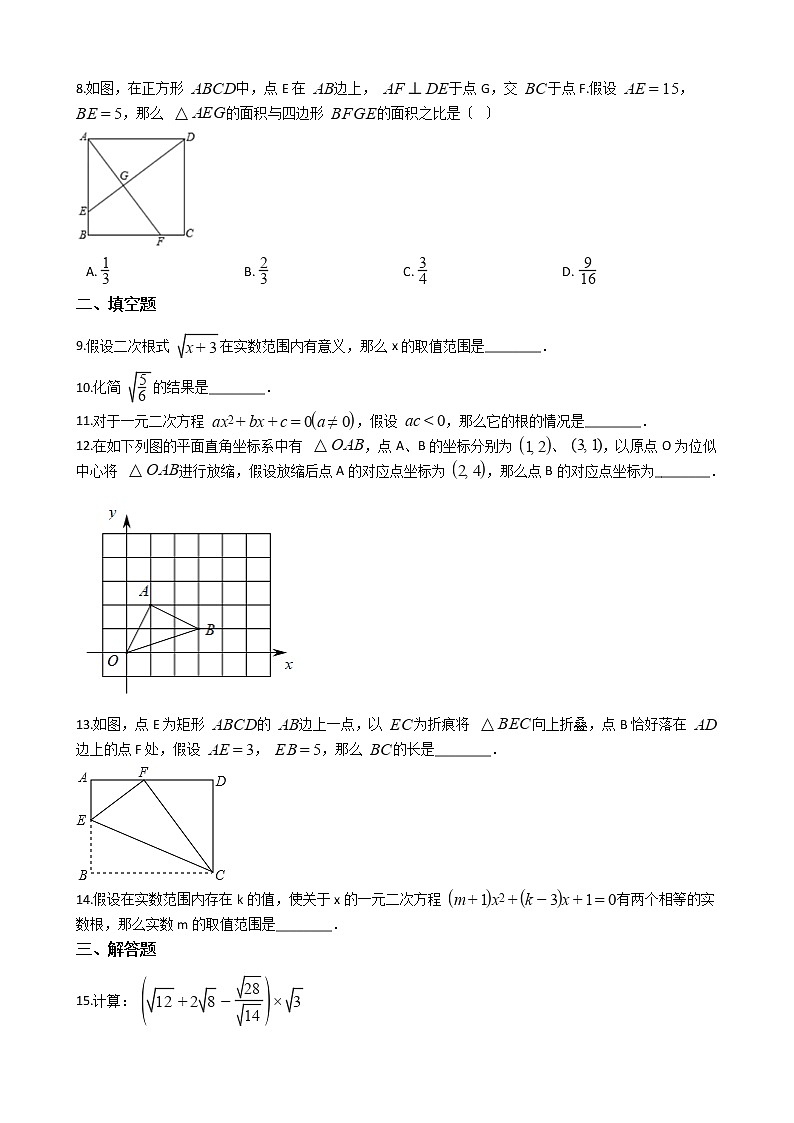
8.如图，在正方形 中，点E在 边上， 于点G，交 于点F.假设 ， ，那么 的面积与四边形 的面积之比是〔  〕

A.                                          B.                                          C.                                          D. 
二、填空题
9.假设二次根式 在实数范围内有意义，那么x的取值范围是________．
10.化简 的结果是________．
11.对于一元二次方程 ，假设 ，那么它的根的情况是________．
12.在如下列图的平面直角坐标系中有 ，点A、B的坐标分别为 、 ，以原点O为位似中心将 进行放缩，假设放缩后点A的对应点坐标为 ，那么点B的对应点坐标为________．

13.如图，点E为矩形 的 边上一点，以 为折痕将 向上折叠，点B恰好落在 边上的点F处，假设 ， ，那么 的长是________．

14.假设在实数范围内存在k的值，使关于x的一元二次方程 有两个相等的实数根，那么实数m的取值范围是________．
三、解答题
15.计算：
16.解方程：
17.图①、图②、图③均是6×6的正方形网格，每个小正方形的顶点称为格点，点A、B、C、D均在格点上．在图①、图②、图③中，只用无刻度的直尺，在给定的网格中按要求画图，不要求写画法，要求保存必要的作图痕迹．

〔1〕在图①中以线段 为边画一个三角形，使它与 相似．
〔2〕在图②中画一个三角形，使它与 相似〔不全等〕．
〔3〕在图③中的线段 上画一个点P，使 ．
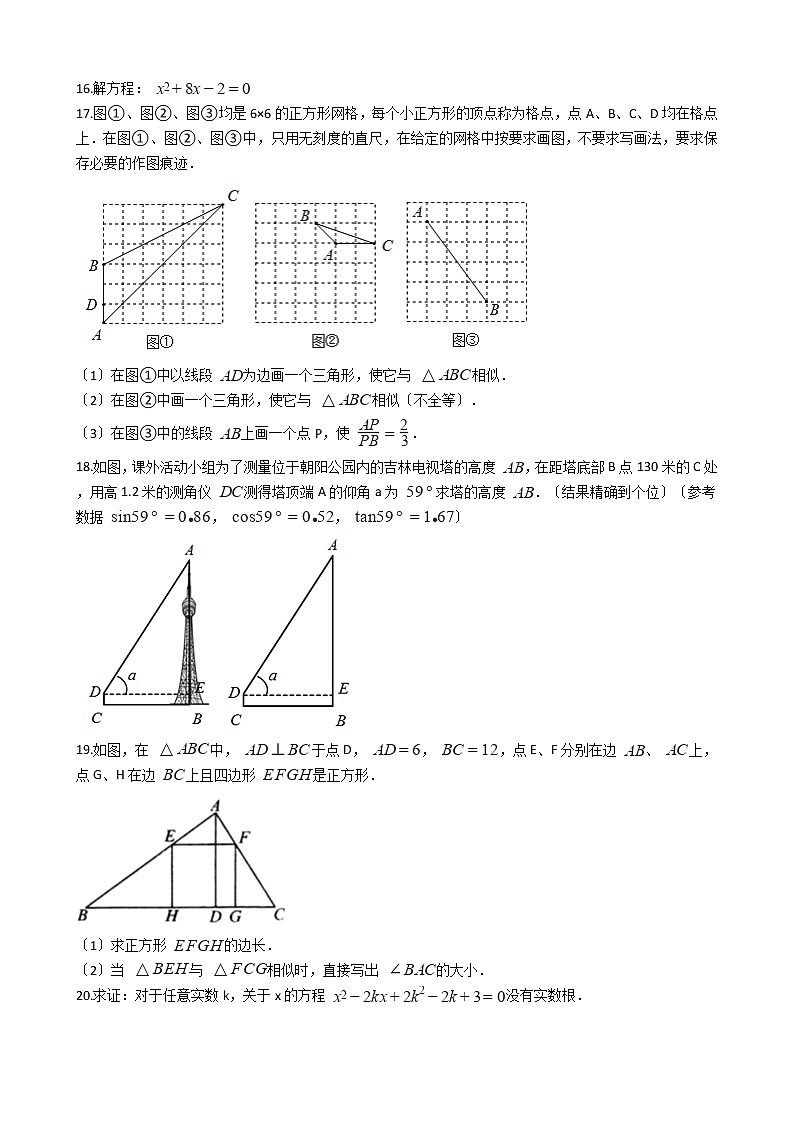
18.如图，课外活动小组为了测量位于朝阳公园内的吉林电视塔的高度 ，在距塔底部B点130米的C处，用高1.2米的测角仪 测得塔顶端A的仰角a为 求塔的高度 ．〔结果精确到个位〕〔参考数据 ， ， 〕

19.如图，在 中， 于点D， ， ，点E、F分别在边 、 上，点G、H在边 上且四边形 是正方形．

〔1〕求正方形 的边长．
〔2〕当 与 相似时，直接写出 的大小．
20.求证：对于任意实数k，关于x的方程 没有实数根．
21.小明同学在2021年秋季升入七年级时的身高是 ，在2021年秋季升入九年级时的身高是 ，求这两年小明身高的年平均增长率．假设在未来的一年里小明身高按这个增长率的一半增长，到2021年秋季升入高中一年级时的身高将是多少？〔结果精确到个位〕
22.如图①，在四边形 中， ，P是对角线 的中点，M是 的中点，N是 的中点．
〔1〕求证： ．
 
〔2〕如图②，在上边题目的条件下，延长上图中的线段 交 的延长线于点E，延长线段 交 的延长线于点F.求证： ．

〔3〕假设〔1〕中的 ，那么 的大小为________．
23.先阅读下面框中方程的求解过程，然后解答问题．
解方程 ．
解：设 ，那么 ，原方程可化为 ．
两边同乘以t，化简得， ．
解这个方程，得 ， ．
当 时，解得 ， ．
当 时，此方程没有实数根．
经检验， ， 是原方程的解．
所以方程 的解为：
， ．
〔1〕解方程 ．
〔2〕直接写出方程 的解．
24.如图，在 中， 于点D， ， ， ，点P是 边上一点〔不与点B、D、C重合〕，过点P作 交 或 于点Q，作点Q关于直线 的对称点M，连结 ，过点M作 交直线 于点N．设 ，矩形 与 重叠局部图形的周长为y．

〔1〕直接写出 的长〔用含x的代数式表示〕．
〔2〕求矩形 成为正方形时x的值．
〔3〕求y与x的函数关系式.
〔4〕当过点C和点M的直线平分 的面积时，直接写出x的值．

答案解析局部
一、单项选择题
1.【答案】 A
【解析】【解答】 = =3
故答案为：A．

【分析】根据二次根式的性质求解即可。
2.【答案】 B
【解析】【解答】A、 ，被开方数含能开得尽方的因数，不是最简二次根式，故本选项不符合题意；
B、 符合最简二次根式的定义，是最简二次根式，故本选项符合题意；
C、 ，被开方数含能开得尽方的因数，不是最简二次根式，故本选项不符合题意；
D、 ，该二次根式的被开方数是小数，不是最简二次根式，故本选项不符合题意；
故答案为：B

【分析】利用最简二次根式的定义逐项判定即可。
3.【答案】 A
【解析】【解答】∵
∴
方程 的二次项系数为1，一次项系数为−3，常数项为-4，
故答案为：A．

【分析】根据一元二次方程的定义求解即可。
4.【答案】 C
【解析】【解答】解：方程 变形为 ，

∴
故答案为：C
【分析】利用配方法逐项判定即可。
5.【答案】 D
【解析】【解答】∵
∴2a=3b，a= b
∴ = =3
故答案为：D．
【分析】根据比例的性质，利用设k法求解即可。
6.【答案】 B
【解析】【解答】∵OA=3OD，OB=3OC，
∴ ，
∵AD与BC相交于点O，
∴∠AOB=∠DOC，
∴△AOB∽△DOC，
∴ ，
∵
∴CD= cm,
故答案为：B.
【分析】根据题意利用两组对边的比相等且夹角相等的三角形是相似三角形，再利用相似三角形的性质求解即可。
7.【答案】 D
【解析】【解答】∵
∴ ，即
解得：BC＝8
∴AC＝AB＋BC＝4＋8＝12
故答案为：D

【分析】根据平行线分线段成比例得到， 再代入计算即可。
8.【答案】 D
【解析】【解答】∵四边形ABCD是正方形，
∴∠BAD=∠B=90∘，AB=DA；
∵ ，
∴
∴
∴∠EAG=∠EDA,
∴△AED≌△BFA〔ASA〕；
∴ ；
∴ ,即 ；
∵∠EAG=∠EDA,∠AGE=∠DGA=90∘，
∴△AEG∽△DAG；
∴
∴ 的面积与四边形 的面积之比是 ,
故答案为：D.

【分析】首先证明△AED≌△BFA，得到， 两者都减去△AEG的面积后得到， 那么只要求出△AEC和△AGD的面积关系即可；再Rt△AED中，AG⊥ED，证明出△AEG∽△DAG，根据相似比求出面积之比即可。
二、填空题
9.【答案】 x≥-3
【解析】【解答】由题意得，x+3≥0，
解得x≥-3．

【分析】根据二次根式有意义的条件得到不等式求解即可。
10.【答案】
【解析】【解答】解： ．
故答案为： ．

【分析】利用分母有理化，分子分母同乘即可。
11.【答案】 方程有两个不相等的实数根
【解析】【解答】解：△=b2-4ac，
∵ac＜0，
∴-ac＞0，
而b2≥0，
∴△＞0，
∴方程有两个不相等的实数根．
故答案为：方程有两个不相等的实数根．

【分析】利用一元二次方程根的判别式求出不等式求解即可。
12.【答案】 〔6，2〕
【解析】【解答】∵以原点O为位似中心将 进行放缩，A 放缩后对应点坐标为 ，
∴相似比为1：2，
∵B
∴B的对应点坐标为〔6,2〕，
故答案为：〔6，2〕.

【分析】先根据点A的坐标求出相似比，再利用相似比求出点B的对应点坐标即可。
13.【答案】 10
【解析】【解答】∵折叠， ， ，
∴EF=5，BC=FC
∴AF=
设BC为x，那么AD=x=FC，DF=x-4,
由CD=AB=AE+BE=8
∴在Rt△CDF中得到FC2=DF2+CD2 ，
故x2=〔x-4〕2+82 ，
解得x=10
即BC=10
故答案为：10．

【分析】根据折叠与勾股定理的性质求出AF=4，设BC为x，那么AD=x-4，在Rt△CDF中得到FC2=DF2+CD2，再代入计算求解即可。
14.【答案】 m＞-1
【解析】【解答】依题意可得
∴ ≥0
∴m＞-1
故答案为：m＞-1．

【分析】根据一元二次方程根的判别式列出方程和不等式求解即可。
三、解答题
15.【答案】 解：
＝
＝
＝
＝ ．
【解析】【分析】利用乘法运算律展开，再利用二次根式的运算求解即可。
16.【答案】 解：




∴ ， ．
【解析】【分析】利用配方法的运算方法求解即可。
17.【答案】 〔1〕解：如图①；


〔2〕解：如图②；


〔3〕解：如图③．

【解析】【分析】〔1〕连接DE，那么DE//BC，由相似三角形的判定方法可知△ADE∽△ABC；〔2〕根据勾股定理和相似三角形的判定方法可知△DEF∽△ABC；〔3〕连接DE，BE，DE交AB于点P，那么DE//BC，根据平行线分线段成比例列出比例式求解即可。
18.【答案】 解：∵CD⊥BC，AB⊥BC．DE⊥AB
∴四边形BCDE是矩形
∴BC＝DE＝130米，BE＝CD＝1.2〔米〕
在Rt△ADE中，
∵DE＝130米，∠ADE＝59°
∴AE＝DE·tan59°≈130×1.67＝217.1〔米〕
∴AB＝AE＋BE＝217.1＋1.2＝218.3≈218〔米〕
答：塔的高度 是218米．
【解析】【分析】根据题意可知，在直角三角形中，根据角和邻边，直接根据正切求出对边，继而即可解决问题。
19.【答案】 〔1〕解：如图：

∵四边形 是正方形
∴EF BC，
∴△AEF∽△ABC
设正方形 的边长为x，故EF=EH=DH=x，AH=AD-DH=6-x
∴ ,即
解得x=4
∴正方形 的边长为4；

〔2〕解：设BH=y，那么CG=BC-BG=8-y
当 ∽ ， ,故
解得y=4
∴BH=EH,FG=GC
那么△BEH和△FCG都是等腰直角三角形
∴∠B=∠C=45°
∴ =180°-∠B-∠C=90°
当 ∽ ， ,故
解得y=4．
同理 =90°
故 =90°．
【解析】【分析】〔1〕根据四边形EFGH是正方形得到EF//BC，得到 △AEF∽△ABC ， 设正方形  的边长为x，故EF=EH=DH=x，AH=AD-DH=6-x ，再根据相似三角形的性质列出比例式求解即可；〔2〕 设BH=y，那么CG=BC-BG=8-y ，分两种情况讨论： 当  ∽   ，   当  ∽   ，   列出比例式求解即可。
20.【答案】 证明：∵


＜0
∴对于任意实数k，关于x的方程 没有实数根．
【解析】【分析】利用一元二次方程根的判别式求解，最后结果跟0比较即可。
21.【答案】 解：设年平均增长率为x,根据题意得
解得x1=0.1,x2=-2.1
∴年平均增长率为10%
∵在未来的一年里小明身高按这个增长率的一半增长，
∴2021年秋季升入高中一年级时的身高 ≈178cm．
【解析】【分析】 设年平均增长率为x, 根据题意列出一元二次方程求出平均增长率，因此得到2021年秋季升入高中一年级时的身高。
22.【答案】 〔1〕解：∵P是对角线BD的中点，M是DC的中点，N是AB的中点，
∴PM、PN分别是△BCD和△ABD的中位线，
∴PM＝ BC，PN＝ AD，
∵AD＝BC，
∴PM＝PN，
∴∠PMN＝∠PNM．

〔2〕解：由〔1〕可得∠PMN＝∠PNM，MP BF,AE NP
∴ ,
∴

〔3〕29°
【解析】【解答】〔3〕 =x°，由〔2〕得 =x，
∴∠FNB= ，
在△BNF中∠ABC+∠F+∠FNB=180°
∴∠ABC+x+ =180°
∴122°+2x=180°
解得x=29
∴ =29°
故答案为：29°．

【分析】〔1〕根据三角形的中位线的性质得到 PM＝  BC，PN＝  AD， 再利用等边对等角求解即可；〔2〕利用同〔1〕的方法即可证出结论；〔3〕设=x°，由〔2〕得 =x，再利用三角形的内角和求解即可。
23.【答案】 〔1〕解：设x2-x=y，那么原方程化为y2-4y+3=0，
所以〔y-1〕〔y-3〕=0，
所以y=1或y=3．
当y=1时，x2-x=1，
整理，得x2-x-1=0．
解得x= ．
所以x1= ，x2= ．
当y=3时，x2-x=3，
整理，得x2-x-3=0．
解得x= ．
所以x3= ，x4= ．
综上所述，原方程的解为：x1= ，x2= ，x3= ，x4= ．

〔2〕解：设 ，那么原方程变形为
整理为：
解得， ， ，
经检验， ， 均为方程 的解，
当 时， ，整理得 ，
解得， ， 〔舍去〕，
当 时， ，整理得 ，
解得， ， ，
经检验 或 或 是原方程的解，
∴ 或 或
【解析】【分析】〔1〕 设x2-x=y，那么原方程化为y2-4y+3=0， 求出y的值，再求x的值即可；〔2〕 设   ， 那么原方程变形为 ，求出t的值，再求x的值即可。
24.【答案】 〔1〕解：①当PQ交AB于点Q时，0