

初中数学苏科版八年级下册11.3用 反比例函数解决问题课时作业
展开绝密★启用前
11.3用反比例函数解决问题同步练习苏科版初中数学八年级下册
学校:___________姓名:___________班级:___________考号:___________
注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。
一、选择题(本大题共12小题,共36.0分)
- 为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自年月开始限产进行治污改造,其月利润万元与月份之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是
A. 月份的利润为万元
B. 治污改造完成后每月利润比前一个月增加万元
C. 治污改造完成前后共有个月的利润低于万元
D. 月份该厂利润达到万元
- 正比例函数与反比例函数的图象相交于,两点,轴于点,轴于点如图,则四边形的面积为
A.
B.
C.
D.
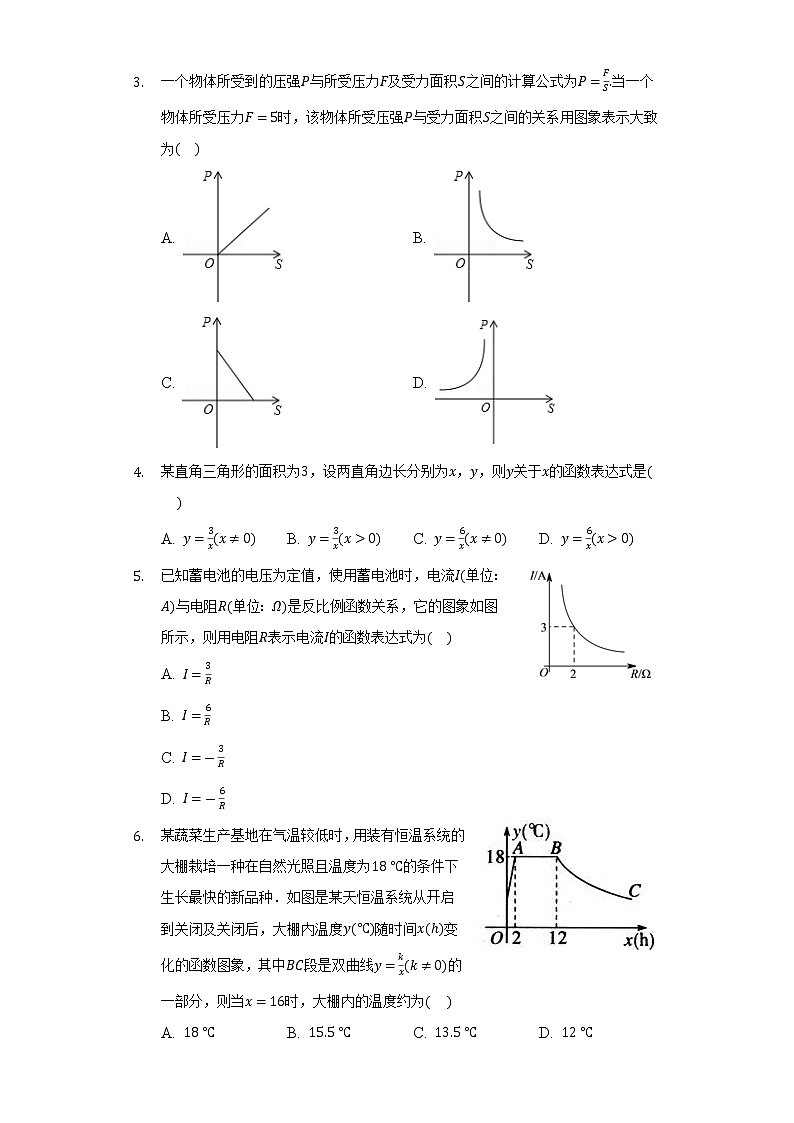
- 一个物体所受到的压强与所受压力及受力面积之间的计算公式为当一个物体所受压力时,该物体所受压强与受力面积之间的关系用图象表示大致为
A. B.
C. D.
- 某直角三角形的面积为,设两直角边长分别为,,则关于的函数表达式是
A. B. C. D.
- 已知蓄电池的电压为定值,使用蓄电池时,电流单位:与电阻单位:是反比例函数关系,它的图象如图所示,则用电阻表示电流的函数表达式为
A.
B.
C.
D.
- 某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度随时间变化的函数图象,其中段是双曲线的一部分,则当时,大棚内的温度约为
A. B. C. D.
- 某物体对地面的压力为定值,物体对地面的压强与受力面积之间的函数关系为,如图所示,那么当时,的变化为
A.
B. 定值
C. 逐渐变小
D. 无法判断
- 一司机驾驶汽车从甲地去乙地,他以千米时的平均速度用了小时到达目的地,当他按原路匀速返回时,汽车的速度千米时与时间小时的函数关系为
A. B. C. D.
- 一司机驾驶汽车从甲地去乙地,他以平均千米时的速度用了个小时到达乙地,当他按原路匀速返回时,汽车的速度千米时与时间小时的函数关系是
A. B. C. D.
- 已知蓄电池的电压为定值,使用蓄电池时,电流单位:与电阻单位:是反比例函数关系,它的图象如图所示,则这个反比例函数的解析式为
A.
B.
C.
D.
- 科学证实:近视眼镜的度数度与镜片焦距成反比例关系,如果度近视镜片的焦距为,则表示与函数关系的图象大致是
A. B.
C. D.
- 购买只茶杯需元,则一只茶杯的价格元与的函数表达式为
A. 取实数 B. 取整数
C. 取自然数 D. 取正整数
二、填空题(本大题共5小题,共15.0分)
- 如图,一次函数与反比例函数的图象交于点,,点在以为圆心,为半径的上,是的中点,若长的最大值为,则的值为______.
|
- 市政府计划建设一项水利工程,某运输公司承包了这项工程运送土石方的任务该运输公司平均每天的工作量与完成运送任务所需的时间天之间的函数图象如图所示若该公司确保每天运送土石方,则公司完成全部运送任务需 天
|
- 车从甲地驶往乙地,行完全程所需的时间与行驶的平均速度之间的反比例函数关系如图所示.若列车要在内到达,则速度至少需要提高到______.
- 由人完成报酬共为元的某项任务,若人均报酬元不少于元,且为整数,则完成此任务的人数的值为______.
- 已知蓄电池的电压为定值,使用蓄电池时,电流与电阻之间成反比例函数关系,它的图像如图所示如果以此蓄电池为电源的用电器,其限制电流不能超过,那么用电器可变电阻应控制的范围是 .
|
三、解答题(本大题共6小题,共48.0分)
- 已知一艘轮船上装有吨货物,轮船到达目的地后开始卸货.设平均卸货速度为单位:吨小时,卸完这批货物所需的时间为单位:小时.
求关于的函数表达式.
若要求不超过小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?
- 如图,在平面直角坐标系中正比例函数与函数的图象相交点,轴于点平移直线,使其经过点,得到直线求直线所对应的函数表达式.
|
- 某工厂生产化肥的总任务一定,平均每天化肥产量吨与完成生产任务所需要的时间天之间成反比例关系,如果每天生产化肥吨,那么完成总任务需要天.
求关于的函数表达式
若要天完成总任务,则每天产量应达到多少
- 由于天气炎热,为预防“蚊虫叮咬”,某校根据学校卫生工作条例,对教室进行“熏药消毒”已知药物在燃烧机释放过程中,室内空气中每立方米含药量毫克与燃烧时间分钟之间的关系如图所示即图中线段和双曲线在点及其右侧的部分
求点的坐标.
若空气中每立方米的含药量达到毫克以上包括毫克时能有效消毒,请问有效消毒的时间有多长?
- 泡茶需要将电热水壶中的水先烧到,然后停止烧水,等水温降低到适合的温度时再泡茶,烧水时水温与时间成一次函数关系;停止加热过了分钟后,水壶中水的温度与时间近似于反比例函数关系如图已知水壶中水的初始温度是,降温过程中水温不低于.
分别求出图中所对应的函数关系式,并且写出自变量的取值范围:
从水壶中的水烧开降到就可以泡茶,问从水烧开到泡茶需要等待多长时间?
- 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压单位:千帕随气体体积单位:立方米的变化而变化,随的变化情况如下表所示.
写出符合表格数据的关于的函数表达式______;
当气球的体积为立方米时,气球内气体的气压为多少千帕?
当气球内的气压大于千帕时,气球将爆炸,依照中的函数表达式,基于安全考虑,气球的体积至少为多少立方米?
答案和解析
1.【答案】
【解析】解:、设反比例函数的解析式为,
把代入得,,
反比例函数的解析式为:,
当时,,
月份的利润为万元,故此选项正确,不合题意;
B、治污改造完成后,从月到月,利润从万到万,故每月利润比前一个月增加万元,故此选项正确,不合题意;
C、当时,则,
解得:,
设一次函数解析式为:,
则,
解得:,
故一次函数解析式为:,
当时,则,
则只有月,月,月,共个月的利润低于万元,故此选项不正确,符合题意.
D、一次函数解析式为:,
故时,,
解得:,
则治污改造完成后的第个月,即月份该厂利润达到万元,故此选项正确,不合题意.
故选:.
直接利用已知点求出一次函数与反比例函数的解析式进而分别分析得出答案.
此题主要考查了一次函数与反比例函数的应用,正确得出函数解析式是解题关键.
2.【答案】
【解析】解:解方程组 得,
即:正比例函数与反比例函数的图象相交于两点的坐标分别为
所以点的坐标为,点的坐标为
因为,轴于点,轴于点
所以,与均是直角三角形
则:,
即:四边形的面积是
联立正比例函数与反比例函数的解析式,解方程组得点、、、的坐标,然后在求四边形的面积.
本题考查了反比例函数与一次函数的交点问题,解题的关键是理解反比例函数与一次函数的图形的交点坐标是其解析式联立而成的方程组的解
3.【答案】
【解析】解:当一定时,与之间成反比例函数,则函数图象是双曲线,同时自变量是正数.
故选:.
根据实际意义以及函数的解析式,根据函数的类型,以及自变量的取值范围即可进行判断.
此题主要考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用实际意义确定其所在的象限.
4.【答案】
【解析】略
5.【答案】
【解析】
【分析】
此题主要考查了待定系数法求反比例函数解析式有关知识,根据函数图象可用电阻表示电流的函数解析式为,再把代入可得的值,进而可得函数解析式.
【解答】
解:设用电阻表示电流的函数解析式为,
过,
,
.
故选B.
6.【答案】
【解析】
【分析】
此题主要考查了反比例函数的应用,求出反比例函数解析式是解题关键,利用待定系数法求反比例函数解析式后将代入函数解析式求出的值即可.
【解答】
解:点在双曲线上,
,
解得:;
当时,,
所以当时,大棚内的温度约为,
故选C.
7.【答案】
【解析】解:根据函数中的,
随着的增大而减小,
当时,
压强逐渐变小,
故选:.
根据函数的图象利用数形结合的方法可以得到压强的变化趋势.
本题考查了反比例函数的应用,解题时可以结合图象得到也可以根据函数的解析式求得.
8.【答案】
【解析】
【分析】
本题考查了根据实际问题列反比例函数关系式,重点是找出题中的等量关系.先求得路程,再由等量关系“速度路程时间”列出关系式即可.
【解答】
解:由于以千米时的平均速度用了小时到达目的地,那么路程为千米,
汽车的速度千米时与时间小时的函数关系为.
故选:.
9.【答案】
【解析】
【分析】
本题考查了根据实际问题列出反比例函数关系式.先利用“以平均千米小时的速度用了个小时到达乙地”求出路程,再列出解析式.
【解答】
解:由题意路程,
故与的关系为.
故选B.
10.【答案】
【解析】解:设,把代入得:
,
故这个反比例函数的解析式为:.
故选:.
直接利用待定系数法求出反比例函数解析式即可.
此题主要考查了反比例函数的应用,正确得出函数解析式是解题关键.
11.【答案】
【解析】略
12.【答案】
【解析】略
13.【答案】
【解析】解:连接,
由对称性得:,
是的中点,
,
长的最大值为,
长的最大值为,
如图,当过圆心时,最长,过作轴于,
,
,
在直线上,
设,则,,
在中,由勾股定理得:,
,
舍或,
,
点在反比例函数的图象上,
;
故答案为:.
作辅助线,先确定长的最大时,点的位置,当过圆心时,最长,设,则,,根据勾股定理计算的值,可得的值.
本题考查了反比例函数与一次函数的交点问题、圆的性质,勾股定理的应用,有难度,解题的关键:利用勾股定理建立方程解决问题.
14.【答案】
【解析】见答案
15.【答案】
【解析】解:从甲地驶往乙地的路程为,
汽车行驶完全程所需的时间与行驶的平均速度之间的关系式为,
当时,即,
,
答:列车要在内到达,则速度至少需要提高到.
故答案为:.
依据行程问题中的关系:时间路程速度,即可得到汽车行驶完全程所需的时间与行驶的平均速度之间的关系式,把代入即可得到答案.
本题考查了反比例函数的应用,找出等量关系是解决此题的关键.
16.【答案】、、
【解析】解:由人完成报酬共为元的某项任务,
,
即:,
人均报酬元不少于元,且为整数,
、、.
故答案为:、、.
首先确定与之间的函数关系,然后代入的值求的整数值即可.
本题考查了反比例函数的应用,解题的关键是能够确定两个变量之间的函数关系,难度不大.
17.【答案】
【解析】略
18.【答案】解:由题意可得:,
则;
不超过小时卸完船上的这批货物,
,
则,
答:平均每小时至少要卸货吨.
【解析】此题主要考查了反比例函数的应用,正确得出函数关系式是解题关键.
直接利用进而得出答案;
直接利用要求不超过小时卸完船上的这批货物,进而得出答案.
19.【答案】解:函数的图象过点,
代入得:,
即,
轴于点,
,
把代入得:,
解得:,
即,
平移直线,使其经过点,
设直线所对应的函数表达式是,
把代入得:,
解得:,
所以直线所对应的函数表达式是.
【解析】求出点的坐标,求出点的坐标,再用待定系数法求出正比例函数的解析式,最后求出一次函数的解析式即可.
本题考查了平移的性质,反比例函数图象上点的坐标特征,用待定系数法求函数的解析式等知识点,能用待定系数法求出函数的解析式是解此题的关键.
20.【答案】解:设,
根据题意得:,
每天生产化肥产量吨与完成生产任务所需要的时间天之间的函数解析式为;
当时,吨,
即若要天完成总任务,则每天产量应达到吨.
【解析】本题考查了反比例函数的应用,解题的关键是求出反比例函数解析式.
首先设出反比例函数为,根据题意求得的值即可;
代入求得值即可.
21.【答案】解:设反比例函数解析式为,
将代入解析式得,,
则函数解析式为,
把代入中得,,
,
;
设正比例函数解析式为,
将代入上式即可求出的值,
,
则正比例函数解析式为,
当时,或,
解得:或,
有效消毒的时间为分钟.
【解析】设反比例函数解析式为,将代入解析式即可得到结论;
设正比例函数解析式为,将代入上式即可求出的值,求得正比例函数解析式为,当时,得到或,于是得到结论.
本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
22.【答案】解:停止加热分钟后,设,
由题意得:,
解得:,
,
当时,解得:,当时,,
点坐标为,
点坐标为,
当加热烧水时,设,
由题意将点坐标代入上式得,
解得:,
当加热烧水时,函数关系式为;
当停止加热时与的函数关系式为;;
把代入,得,
因此从水壶中的水烧开降到可以泡茶需要等待分钟.
【解析】本题考查了反比例函数的解析式,解题的关键是从实际问题中整理出反比例函数的模型,难度不大.
将点的坐标代入反比例函数的一般形式利用待定系数法确定反比例函数的解析式,然后求得点和点的坐标,从而用待定系数法确定一次函数的解析式;
将代入反比例函数的解析式,从而求得答案.
23.【答案】解:;
把代入得:,
当气球的体积为立方米时,气球内的气压是千帕;
把代入得,,
故时,,
答:气球的体积应不小于立方米.
【解析】
【分析】
此题主要考查了反比例函数的应用.解题的关键是根据实际意义列出函数关系式,从实际意义中找到对应的变量的值,利用待定系数法求出函数解析式.会用不等式解决实际问题.
设与的函数的解析式为利用待定系数法求函数解析式即可;
把代入可得;
把代入得,所以可知当气球内的气压千帕时,气球将爆炸,为了安全起见,气球的体积应不小于立方米.
【解答】
解:设与的函数的解析式为,
把点代入,
解得.
这个函数的解析式为;
故答案为;
见答案
苏科版八年级下册11.3用 反比例函数解决问题第2课时同步达标检测题: 这是一份苏科版八年级下册11.3用 反比例函数解决问题第2课时同步达标检测题,共6页。试卷主要包含了4L等内容,欢迎下载使用。
初中数学苏科版八年级下册11.3用 反比例函数解决问题第1课时课堂检测: 这是一份初中数学苏科版八年级下册11.3用 反比例函数解决问题第1课时课堂检测,共6页。
初中数学苏科版八年级下册11.3用 反比例函数解决问题复习练习题: 这是一份初中数学苏科版八年级下册11.3用 反比例函数解决问题复习练习题,共15页。试卷主要包含了5;,5.等内容,欢迎下载使用。













