北师大版数学九年级上册期末模拟试卷08（含答案）

这是一份北师大版数学九年级上册期末模拟试卷08（含答案），共27页。试卷主要包含了选择题，四象限，解答题等内容，欢迎下载使用。
1．若反比例函数y=﹣的图象经过点A（2，m），则m的值是（ ）
A．B．2C．﹣D．﹣2
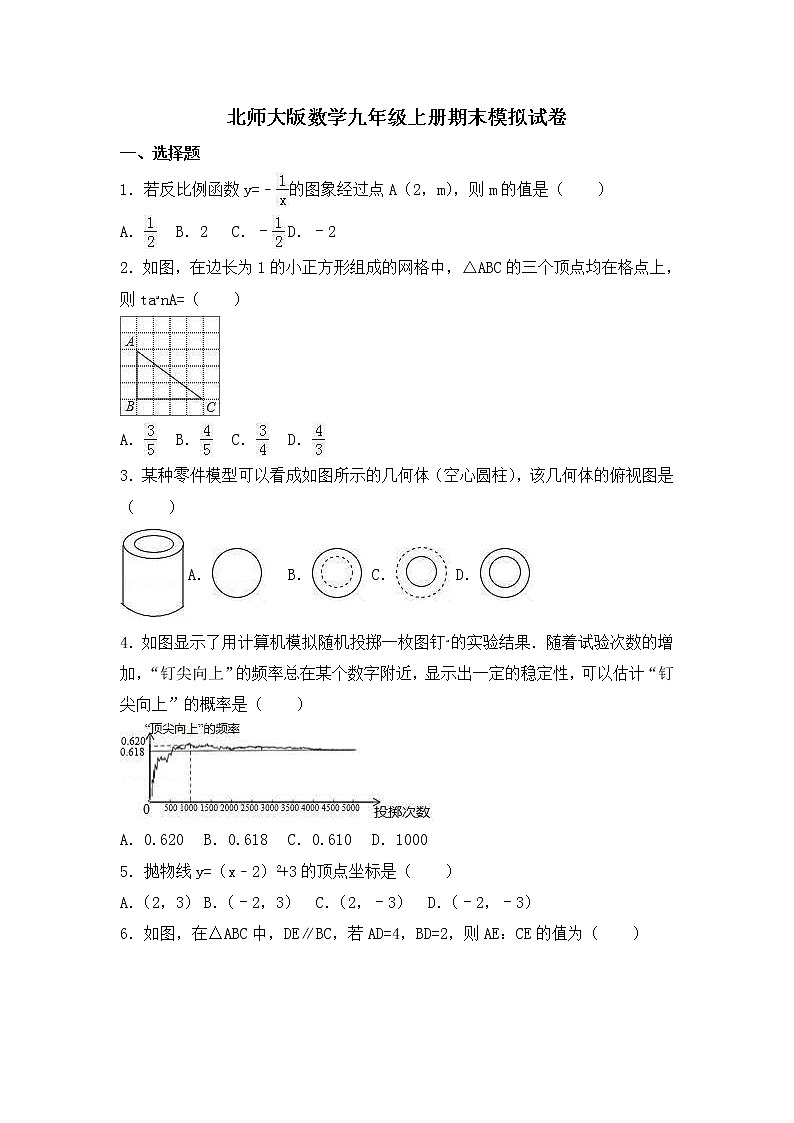
2．如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则tanA=（ ）
A．B．C．D．
3．某种零件模型可以看成如图所示的几何体（空心圆柱），该几何体的俯视图是（ ）
A．B．C．D．
4．如图显示了用计算机模拟随机投掷一枚图钉的实验结果．随着试验次数的增加，“钉尖向上”的频率总在某个数字附近，显示出一定的稳定性，可以估计“钉尖向上”的概率是（ ）
A．0.620B．0.618C．0.610D．1000
5．抛物线y=（x﹣2）2+3的顶点坐标是（ ）
A．（2，3）B．（﹣2，3）C．（2，﹣3）D．（﹣2，﹣3）
6．如图，在△ABC中，DE∥BC，若AD=4，BD=2，则AE：CE的值为（ ）
A．0.5B．2C．D．
7．对于反比例函数，下列说法正确的是（ ）
A．图象经过点（2，﹣1）
B．图象位于第二、四象限
C．当 x＜0 时，y随 x的增大而减小
D．当 x＞0 时，y 随 x的增大而增大
8．小明不慎把家里的圆形玻璃打碎了，其中四块碎片如图所示，为配到与原来大小一样的圆形玻璃，小明带到商店去的一块玻璃碎片应该是（ ）
A．第①块B．第②块C．第③块D．第④块
9．若k＞4，则关于x的一元二次方程x2+4x+k=0的根的情况是（ ）
A．没有实数根B．有两个相等的实数根
C．有两个不相等的实数根D．无法判断
10．一个矩形的面积为20cm，相邻两边长分别为xcm和ycm，那么y与x的关系式是（ ）
A．y=20xB．C．y=20﹣xD．
11．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，CH⊥AF于点H，那么CH的长是（ ）
A．B．C．D．
12．如图，抛物线y1=（x+1）2+1与y2=a（x﹣4）2﹣3交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于B，C两点，且D，E分别为顶点．则下列结论：
①a=；
②AC=AE；
③△ABD是等腰直角三角形；
④当x＞1时y1＞y2．
其中正确的结论是（ ）
A．①③④B．①③C．①②④D．②
二、填空题：
13．方程x2=9的解为 ．
14．如图，BC是⊙O的直径，点A在圆上，连接AO，AC，∠AOB=64°，
则∠ACB= ．
15．如图，Rt△ABC 中，∠C=90°，BC=1.5，sinA=，则AB= ．
16．如图，小明从二次函数y=ax2+bx+c图象中看出这样四条结论：
①a＞0；②b＞0；③c＞0；④△＞0；
其中正确的有 个．
17．在一只不透明的口袋中放入红球6个，黑球2个，黄球n个，这些球除颜色不同外，其它无任何差别．搅匀后随机从中摸出一个恰好是黄球的概率为，则放入口袋中的黄球总数n= ．
18．如图，已知双曲线y=与直线y=﹣x+6相交于A，B两点，过点A作x轴的垂线与过点B作y轴的垂线相交于点C，若△ABC的面积为8，则k的值为 ．
三、解答题
19．解方程：x2﹣3x+2=0．
20．计算：sin30°+3tan60°﹣cs245°．
21．如图，矩形ABCD中，点P是线段AD上任意一点，点Q为BC上一点，且AP=CQ．
（1）求证：BP=DQ；
（2）若AB=4，且当PD=5时四边形PBQD为菱形．求AD为多少．
22．利用一面墙（墙的长度不限），另三边用50m长的篱笆围成一个面积为200m2的矩形场地，求矩形的长和宽．
23．有3个完全相同的小球，把它们分别标号为1，2，3，放在一个口袋中，随机地摸出一个小球不放回，再随机地摸出一个小球．
（1）采用树形图法（或列表法）列出两次摸球出现的所有可能结果；
（2）求摸出的两个球号码之和等于5的概率．
24．如图，AB是⊙O的直径，C是⊙O上一点，D在AB的延长线上，且∠BCD=∠A．
（1）求证：CD是⊙O的切线；
（2）若⊙O的半径为3，CD=4，求BD的长．
25．如图，排球运动员站在点O处练习发球，将球从O点正上方2m的A处发出，把球看成点，其运行的高度y（m）与运行的水平距离x（m）满足关系式y=a（x﹣6）2+h．已知球网与O点的水平距离为9m，高度为2.43m，球场的边界距O点的水平距离为18m．
（1）当h=2.6时，求y与x的关系式（不要求写出自变量x的取值范围）
（2）当h=2.6时，球能否越过球网？球会不会出界？请说明理由；
（3）若球一定能越过球网，又不出边界，求h的取值范围．
26．（1）【问题发现】
如图1，在Rt△ABC中，AB=AC=2，∠BAC=90°，点D为BC的中点，以CD为一边作正方形CDEF，点E恰好与点A重合，则线段BE与AF的数量关系为
（2）【拓展研究】
在（1）的条件下，如果正方形CDEF绕点C旋转，连接BE，CE，AF，线段BE与AF的数量关系有无变化？请仅就图2的情形给出证明；
（3）【问题发现】
当正方形CDEF旋转到B，E，F三点共线时候，直接写出线段AF的长．
27．如图，O是坐标原点，过点A（﹣1，0）的抛物线y=x2﹣bx﹣3与x轴的另一个交点为B，与y轴交于点C，其顶点为D点．
（1）求b的值以及点D的坐标；
（2）连接BC、BD、CD，在x轴上是否存在点P，使得以A、C、P为顶点的三角形与△BCD相似．若存在，求出点P的坐标；若不存在，说明理由；
（3）动点Q的坐标为（m，1）．
①当△BCQ是以BC为直角边的直角三角形时，求m的值；
②连接OQ、CQ，求△CQO的外接圆半径的最小值，并求出此时点Q的坐标．

参考答案
1．若反比例函数y=﹣的图象经过点A（2，m），则m的值是（ ）
A．B．2C．﹣D．﹣2
【解答】解：∵反比例函数y=﹣的图象经过点A（2，m），
∴2m=﹣1，∴m=﹣，故选：C．
2．如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则tanA=（ ）
A．B．C．D．
【解答】解：在直角△ABC中，∵∠ABC=90°，∴tanA==．
故选：D．
3．某种零件模型可以看成如图所示的几何体（空心圆柱），该几何体的俯视图是（ ）
A．B．C．D．
【解答】解：空心圆柱由上向下看，看到的是一个圆环，并且大小圆都是实心的．
故选：D．

4．如图显示了用计算机模拟随机投掷一枚图钉的实验结果．随着试验次数的增加，“钉尖向上”的频率总在某个数字附近，显示出一定的稳定性，可以估计“钉尖向上”的概率是（ ）
A．0.620B．0.618C．0.610D．1000
【解答】解：由图象可知随着实验次数的增加，“钉尖向上”的频率总在0.618附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是0.618．
故选：B．

5．抛物线y=（x﹣2）2+3的顶点坐标是（ ）
A．（2，3）B．（﹣2，3）C．（2，﹣3）D．（﹣2，﹣3）
【解答】解：y=（x﹣2）2+3是抛物线的顶点式方程，
根据顶点式的坐标特点可知，顶点坐标为（2，3）．
故选：A．

6．如图，在△ABC中，DE∥BC，若AD=4，BD=2，则AE：CE的值为（ ）
A．0.5B．2C．D．
【解答】解：∵DE∥BC，AD=4，DB=2
∴AE：EC=AD：DB=2：1．
故选：B．

7．对于反比例函数，下列说法正确的是（ ）
A．图象经过点（2，﹣1）
B．图象位于第二、四象限
C．当 x＜0 时，y随 x的增大而减小
D．当 x＞0 时，y 随 x的增大而增大
【解答】解：A、把x=2代入y=得，y=1，则（2，﹣1）不在图象上，选项错误；
B、图象位于第一、三象限，选项错误；
C、当x＜0时，y随x的增大而减小，选项正确；
D、当x＞0时，y随x的增大而减小，选项错误．
故选：C．

8．小明不慎把家里的圆形玻璃打碎了，其中四块碎片如图所示，为配到与原来大小一样的圆形玻璃，小明带到商店去的一块玻璃碎片应该是（ ）
A．第①块B．第②块C．第③块D．第④块
【解答】解：第②块出现一段完整的弧，可在这段弧上任做两条弦，作出这两条弦的垂直平分线，就交于了圆心，进而可得到半径的长．
故选：B．

9．若k＞4，则关于x的一元二次方程x2+4x+k=0的根的情况是（ ）
A．没有实数根B．有两个相等的实数根
C．有两个不相等的实数根D．无法判断
【解答】解：
∵x2+4x+k=0，
∴△=42﹣4k=4（4﹣k），
∵k＞4，
∴4﹣k＜0，
∴△＜0，
∴该方程没有实数根，
故选：A．

10．一个矩形的面积为20cm，相邻两边长分别为xcm和ycm，那么y与x的关系式是（ ）
A．y=20xB．C．y=20﹣xD．
【解答】解：根据矩形的面积公式知道x与y成反比例，即：y=．
故选：B．

11．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，CH⊥AF于点H，那么CH的长是（ ）
A．B．C．D．
【解答】解：∵CD=BC=1，
∴GD=3﹣1=2，
∵△ADK∽△FGK，
∴，
即，
∴DK=DG，
∴DK=2×=，GK=2×=，
∴KF=，
∵△CHK∽△FGK，
∴，
∴，
∴CH=．
方法二：连接AC、CF，利用面积法：CH=；
故选：A．

12．如图，抛物线y1=（x+1）2+1与y2=a（x﹣4）2﹣3交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于B，C两点，且D，E分别为顶点．则下列结论：
①a=；
②AC=AE；
③△ABD是等腰直角三角形；
④当x＞1时y1＞y2．
其中正确的结论是（ ）
A．①③④B．①③C．①②④D．②
【解答】解：∵抛物线y1=（x+1）2+1与y2=a（x﹣4）2﹣3交于点A（1，3），
∴3=a（1﹣4）2﹣3，
解得：a=，故①正确；
过点E作EF⊥AC于点F，
∵E是抛物线的顶点，
∴AE=EC，E（4，﹣3），
∴AF=3，EF=6，
∴AE==3，AC=2AF=6，
∴AC≠AE，故②错误；
当y=3时，3=（x+1）2+1，
解得：x1=1，x2=﹣3，
故B（﹣3，3），D（﹣1，1），
则AB=4，AD=BD=2，
∴AD2+BD2=AB2，
∴③△ABD是等腰直角三角形，正确；
∵（x+1）2+1=（x﹣4）2﹣3时，
解得：x1=1，x2=37，
∴当37＞x＞1时，y1＞y2，故④错误．
故选：B．

二、填空题：（本大题共6个小题，每小题4分，共24分．）
13．方程x2=9的解为 ±3 ．
【解答】解：∵x2=9，∴x=±3．

14．如图，BC是⊙O的直径，点A在圆上，连接AO，AC，∠AOB=64°，则∠ACB= 32° ．
【解答】解：∵AO=OC，
∴∠ACB=∠OAC，
∵∠AOB=64°，
∴∠ACB+∠OAC=64°，
∴∠ACB=64°÷2=32°．
故答案为：32°．

15．如图，Rt△ABC 中，∠C=90°，BC=1.5，sinA=，则AB= 3.9 ．
【解答】解：AB=，
故答案为：3.9

16．如图，小明从二次函数y=ax2+bx+c图象中看出这样四条结论：
①a＞0；②b＞0；③c＞0；④△＞0；
其中正确的有 3 个．
【解答】解：∵抛物线开口向上，
∴a＞0，故①正确；
∵对称轴在y轴的左侧，
∴﹣＜0，且a＞0，
∴b＞0，故②正确；
∵抛物线与y轴的交点在x轴的下方，
∴c＜0，故③不正确；
∵抛物线与x轴有两个交点，
∴△=b2﹣4ac＞0，故④正确；
综上可知正确的有3个，
故答案为3．

17．在一只不透明的口袋中放入红球6个，黑球2个，黄球n个，这些球除颜色不同外，其它无任何差别．搅匀后随机从中摸出一个恰好是黄球的概率为，则放入口袋中的黄球总数n= 4 ．
【解答】解：∵口袋中放入红球6个，黑球2个，黄球n个，
∴球的总个数为6+2+n，
∵搅匀后随机从中摸出一个恰好是黄球的概率为，
=，
解得，n=4．
故答案为：4．

18．如图，已知双曲线y=与直线y=﹣x+6相交于A，B两点，过点A作x轴的垂线与过点B作y轴的垂线相交于点C，若△ABC的面积为8，则k的值为 5 ．
【解答】解法一：
解：，
解得：，，
即点A的坐标为（3﹣，3+），
点B的坐标为（3+，3﹣），
则AC=2，BC=2，
∵S△ABC=8，
∴AC•BC=8，
即2（9﹣k）=8，
解得：k=5．
解法二：
解：设点A（x1，6﹣x1），B（x2，6﹣x2）
∵双曲线y=与直线y=﹣x+6相交于A，B两点，
∴方程﹣（﹣x+6）=0有解，
即：x2﹣6x+k=0有2个不相同的实根，
∴x1+x2=6，x1x2=k，
∵AC⊥BC
∴C点坐标为（x1，6﹣x2）
∴AC=x2﹣x1 BC=x2﹣x1
∵S△ABC=8，
∴AC•BC=8
∴（x2﹣x1）2=8
整理得：（x1+x2）2﹣4x1x2=16，
∴36﹣4k=16
解得k=5，
故答案为：5．
解法三：根据对称性设A（a，b），B（b，a），
由题意：S△ABC=（a﹣b）2=8，
∴a﹣b=﹣4．
又∵a+b=6，
∴a=1，b=5，
∴k=5．

三、解答题（本大题9个小题，共78分．解答应写出文字说明、证明过程或演算步骤．）
19．（5分）解方程：x2﹣3x+2=0．
【解答】解：∵x2﹣3x+2=0，
∴（x﹣1）（x﹣2）=0，
∴x﹣1=0或x﹣2=0，
∴x1=1，x2=2．

20．（5分）计算：sin30°+3tan60°﹣cs245°．
【解答】解：原式=+3×﹣（）2
=+﹣
=．

21．（8分）如图，矩形ABCD中，点P是线段AD上任意一点，点Q为BC上一点，且AP=CQ．
（1）求证：BP=DQ；
（2）若AB=4，且当PD=5时四边形PBQD为菱形．求AD为多少．
【解答】证明：（1）∵四边形ABCD是矩形，
∴∠A=∠C=90°，AB=CD，
在Rt△ABP和Rt△QCD中，
∴△ABP≌△QCD（ASA），
∴BP=DQ；
（2）设AP=a，AD=5+a．
当四边形PBQD是菱形时，PB=PD=5，
在直角△ABP中，根据勾股定理得到AP2+AB2=PB2，即a2+42=52，
可得：a=3，
所以AD=3+5=8．

22．（8分）利用一面墙（墙的长度不限），另三边用50m长的篱笆围成一个面积为200m2的矩形场地，求矩形的长和宽．
【解答】解：设垂直于墙的一边为x米，得：
x（50﹣2x）=200，
解得：x1=20，x2=5．
则另一边为10米或40米．
答：当矩形长为20米时宽为10米，当矩形长为40米时宽为5米．

23．（8分）有3个完全相同的小球，把它们分别标号为1，2，3，放在一个口袋中，随机地摸出一个小球不放回，再随机地摸出一个小球．
（1）采用树形图法（或列表法）列出两次摸球出现的所有可能结果；
（2）求摸出的两个球号码之和等于5的概率．
【解答】解：（1）根据题意，可以画出如下的树形图：
从树形图可以看出，两次摸球出现的所有可能结果共有6种．
（2）设两个球号码之和等于5为事件 A，
摸出的两个球号码之和等于5的结果有2种，
∴出的两个球号码之和等于5的概率为=．

24．（10分）如图，AB是⊙O的直径，C是⊙O上一点，D在AB的延长线上，且∠BCD=∠A．
（1）求证：CD是⊙O的切线；
（2）若⊙O的半径为3，CD=4，求BD的长．
【解答】解：
（1）证明：连接OC．
∵AB是⊙O的直径，C是⊙O上一点，
∴∠ACB=90°，即∠ACO+∠OCB=90°．
∵OA=OC，∠BCD=∠A，
∴∠ACO=∠A=∠BCD，
∴∠BCD+∠OCB=90°，即∠OCD=90°，
∴CD是⊙O的切线．
（2）解：在Rt△OCD中，∠OCD=90°，OC=3，CD=4，
∴OD==5，
∴BD=OD﹣OB=5﹣3=2．

25．（10分）如图，排球运动员站在点O处练习发球，将球从O点正上方2m的A处发出，把球看成点，其运行的高度y（m）与运行的水平距离x（m）满足关系式y=a（x﹣6）2+h．已知球网与O点的水平距离为9m，高度为2.43m，球场的边界距O点的水平距离为18m．
（1）当h=2.6时，求y与x的关系式（不要求写出自变量x的取值范围）
（2）当h=2.6时，球能否越过球网？球会不会出界？请说明理由；
（3）若球一定能越过球网，又不出边界，求h的取值范围．
【解答】解：（1）∵h=2.6，球从O点正上方2m的A处发出，
∴抛物线y=a（x﹣6）2+h过点（0，2），
∴2=a（0﹣6）2+2.6，
解得：a=﹣，
故y与x的关系式为：y=﹣（x﹣6）2+2.6，
（2）当x=9时，y=﹣（x﹣6）2+2.6=2.45＞2.43，
所以球能过球网；
当y=0时，，
解得：x1=6+2＞18，x2=6﹣2（舍去）
故会出界；
（3）当球正好过点（18，0）时，抛物线y=a（x﹣6）2+h还过点（0，2），代入解析式得：
，
解得：，
此时二次函数解析式为：y=﹣（x﹣6）2+，
此时球若不出边界h≥，
当球刚能过网，此时函数解析式过（9，2.43），抛物线y=a（x﹣6）2+h还过点（0，2），代入解析式得：
，
解得：，
此时球要过网h＞，
故若球一定能越过球网，又不出边界，h的取值范围是：h≥．
解法二：y=a（x﹣6）2+h过点（0，2）点，代入解析式得：
2=36a+h，若球越过球网，则当x=9时，y＞2.43，即9a+h＞2.43解得h＞
球若不出边界，则当x=18时，y≤0，解得h≥．
故若球一定能越过球网，又不出边界，h的取值范围是：h≥．

26．（12分）（1）【问题发现】
如图1，在Rt△ABC中，AB=AC=2，∠BAC=90°，点D为BC的中点，以CD为一边作正方形CDEF，点E恰好与点A重合，则线段BE与AF的数量关系为 BE=AF
（2）【拓展研究】
在（1）的条件下，如果正方形CDEF绕点C旋转，连接BE，CE，AF，线段BE与AF的数量关系有无变化？请仅就图2的情形给出证明；
（3）【问题发现】
当正方形CDEF旋转到B，E，F三点共线时候，直接写出线段AF的长．
【解答】解：（1）在Rt△ABC中，AB=AC=2，
根据勾股定理得，BC=AB=2，
点D为BC的中点，
∴AD=BC=，
∵四边形CDEF是正方形，
∴AF=EF=AD=，
∵BE=AB=2，
∴BE=AF，
故答案为BE=AF；
（2）无变化；
如图2，在Rt△ABC中，AB=AC=2，
∴∠ABC=∠ACB=45°，
∴sin∠ABC==，
在正方形CDEF中，∠FEC=∠FED=45°，
在Rt△CEF中，sin∠FEC=，
∴，
∵∠FCE=∠ACB=45°，
∴∠FCE﹣∠ACE=∠ACB﹣∠ACE，
∴∠FCA=∠ECB，
∴△ACF∽△BCE，
∴，
∴BE=AF，
∴线段BE与AF的数量关系无变化；
（3）当点E在线段AF上时，如图2，
由（1）知，CF=EF=CD=，
在Rt△BCF中，CF=，BC=2，
根据勾股定理得，BF=，
∴BE=BF﹣EF=﹣，
由（2）知，BE=AF，
∴AF=﹣1，
当点E在线段BF的延长线上时，如图3，
在Rt△ABC中，AB=AC=2，
∴∠ABC=∠ACB=45°，
∴sin∠ABC==，
在正方形CDEF中，∠FEC=∠FED=45°，
在Rt△CEF中，sin∠FEC=，
∴，
∵∠FCE=∠ACB=45°，
∴∠FCB+∠ACB=∠FCB+∠FCE，
∴∠FCA=∠ECB，
∴△ACF∽△BCE，
∴，
∴BE=AF，
由（1）知，CF=EF=CD=，
在Rt△BCF中，CF=，BC=2，
根据勾股定理得，BF=，
∴BE=BF+EF=+，
由（2）知，BE=AF，
∴AF=+1．
即：当正方形CDEF旋转到B，E，F三点共线时候，线段AF的长为﹣1或+1．

27．（12分）如图，O是坐标原点，过点A（﹣1，0）的抛物线y=x2﹣bx﹣3与x轴的另一个交点为B，与y轴交于点C，其顶点为D点．
（1）求b的值以及点D的坐标；
（2）连接BC、BD、CD，在x轴上是否存在点P，使得以A、C、P为顶点的三角形与△BCD相似．若存在，求出点P的坐标；若不存在，说明理由；
（3）动点Q的坐标为（m，1）．
①当△BCQ是以BC为直角边的直角三角形时，求m的值；
②连接OQ、CQ，求△CQO的外接圆半径的最小值，并求出此时点Q的坐标．
【解答】解：（1）把A（﹣1，0）代入y=x2﹣bx﹣3，得
1+b﹣3=0，
解得b=2．
y=x2﹣2x﹣3=（x﹣1）2﹣4，
∴D（1，﹣4）．
（2）如图1，
当y=0时，x2﹣2x﹣3=0，解得x1=﹣1，x2=3，即A（﹣1，0），B（3，0），D（1，﹣4）．
由勾股定理，得
BC2=18，CD2=1+1=2，BD2=22+16=20，
BC2+CD2=BD2，∠BCD=90°，
①当△APC△DCB时， =，即=，解得AP=1，即P（0，0）；
②当△ACP∽△DCB时， =，即=，解得AP=10，即P′（9，0），
综上所述：点P的坐标（0，0）（9，0）；
（3）①如图2，当x=0时，y=﹣3，即C（0，﹣3）．
又∵B（3，0），
∴当∠QBC=90°，由BC2+BQ2=CQ2得到：32+（﹣3）2+（m﹣3）2+12=（m﹣0）2+（1+3）2，
解得m=2；
当∠QCB=90°，由BC2+CQ2=BQ2得到：32+（﹣3）2+（m﹣0）2+（1+3）2=（m﹣3）2+12，
解得m=4；
综上所述，m的值为2或4；
②如图3，
记△OQC的外心为M，则M在OC的垂直平分线MN上（MN与y轴交与点N）．
∵当MQ取最小值时，
⊙M与直线y=1相切，
MQ=FN=OM=2.5，
MN===2，
FQ=MN=2，
∴Q（2，1）．
根据题意知，（﹣2，1）也满足题意，
综上所述，Q的坐标是（2，1）或Q（﹣2，1）．