2021年江苏省无锡市新吴区中考数学二模试卷 解析版

这是一份2021年江苏省无锡市新吴区中考数学二模试卷 解析版，共31页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2021年江苏省无锡市新吴区中考数学二模试卷
一、选择题（本大题共10小题，每小题3分，共30分．）
1．（3分）2的倒数是（　　）
A．﹣2 B．2 C．﹣ D．
2．（3分）下列图形中，是中心对称图形但不是轴对称图形的是（　　）
A． B． C． D．
3．（3分）下列运算正确的是（　　）
A．（a2）3＝a5 B．a4•a2＝a8 C．a6÷a3＝a2 D．（ab）3＝a3b3
4．（3分）一个几何体的三视图如图所示，则这个几何体是（　　）

A．圆柱 B．圆锥 C．三棱柱 D．长方体
5．（3分）某鞋厂调查了商场一个月内不同尺码男鞋的销量，在平均数、中位数、众数和方差等数个统计量中，该鞋厂最关注的是（　　）
A．平均数 B．中位数 C．众数 D．方差
6．（3分）如图，在半径为的圆形纸片中，剪一个圆心角为90°的最大扇形（阴影部分），则这个扇形的面积为（　　）

A．π B． C．2π D．
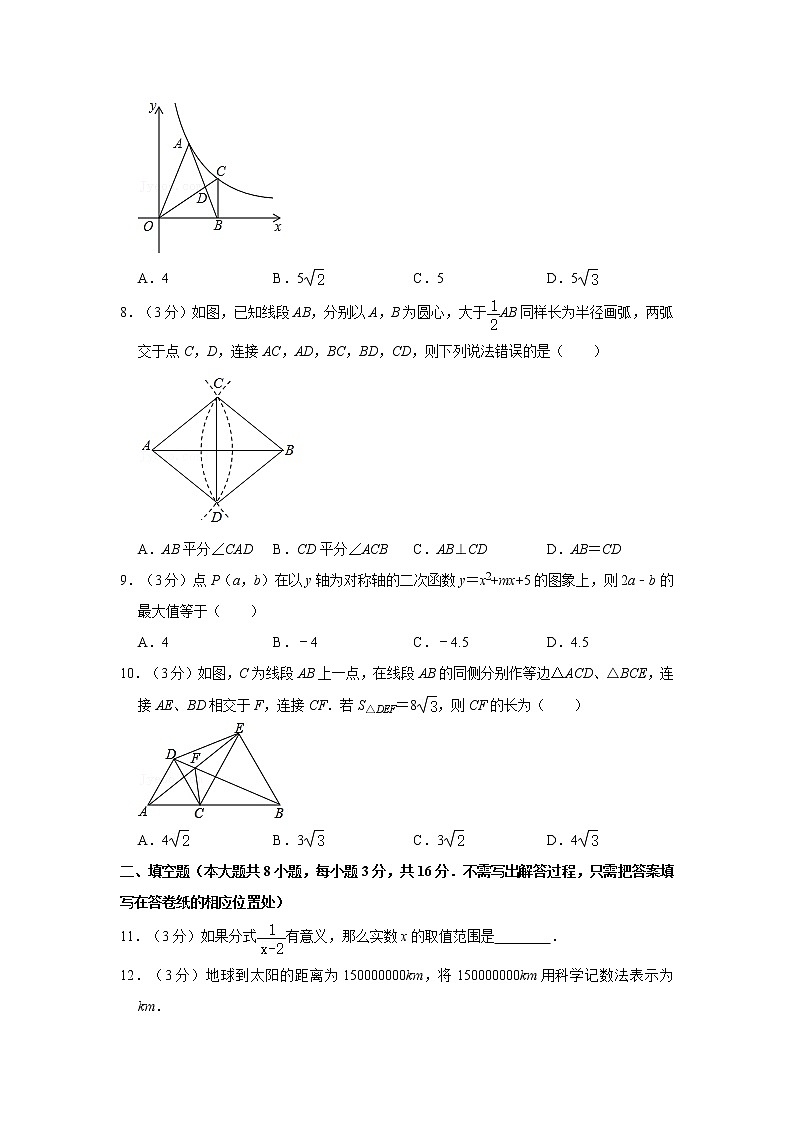
7．（3分）如图，A为反比例函数y＝（其中x＞0）图象上的一点，在x轴正半轴上有一点B，OB＝6．连接OA，AB，且OA＝AB．过点B作BC⊥OB，交反比例函数y＝（其中x＞0）的图象于点C，连接OC交AB于点D，S△OBC＝6，则AB的长度为（　　）

A．4 B．5 C．5 D．5
8．（3分）如图，已知线段AB，分别以A，B为圆心，大于AB同样长为半径画弧，两弧交于点C，D，连接AC，AD，BC，BD，CD，则下列说法错误的是（　　）

A．AB平分∠CAD B．CD平分∠ACB C．AB⊥CD D．AB＝CD
9．（3分）点P（a，b）在以y轴为对称轴的二次函数y＝x2+mx+5的图象上，则2a﹣b的最大值等于（　　）
A．4 B．﹣4 C．﹣4.5 D．4.5
10．（3分）如图，C为线段AB上一点，在线段AB的同侧分别作等边△ACD、△BCE，连接AE、BD相交于F，连接CF．若S△DEF＝8，则CF的长为（　　）

A．4 B．3 C．3 D．4
二、填空题（本大题共8小题，每小题3分，共16分．不需写出解答过程，只需把答案填写在答卷纸的相应位置处）
11．（3分）如果分式有意义，那么实数x的取值范围是　 　．
12．（3分）地球到太阳的距离为150000000km，将150000000km用科学记数法表示为　 　km．
13．（3分）正十边形一个内角度数为　 　．
14．（3分）若一组数据3，4，5，x，6，7的平均数是5，则x的值是　 　．
15．（3分）如图是某商场营业大厅自动扶梯示意图．自动扶梯AB的倾斜角为30°，在自动扶梯下方地面C处测得扶梯顶端B的仰角为60°，A、C之间的距离为4m．则自动扶梯的垂直高度BD＝　 　m．（结果保留根号）

16．（3分）如图，菱形ABOC的边AB，AC分别与⊙O相切于点D，E．若点D是AB的中点，则∠DOE＝　 　°．

17．（3分）把一张宽为2cm的长方形纸片ABCD折叠成如图所示的阴影图案，顶点A，D互相重合，中间空白部分是以E为直角顶点，腰长为4cm的等腰直角三角形，则纸片的长AD为 　 　cm．

18．（3分）如图，在平面直角坐标系中，A（3，0），B（0，4），M为AB边上的一动点，N（0，1），连接MN，将△ABO绕点O逆时针旋转一周，则MN的取值范围为 　 　．

三、解答题（本大题共10小题，共84分．请在答卷相应的区域内作答，解答时应写出文字说明、证明过程或演算步骤．）
19．（8分）计算：
（1）2sin45°﹣（﹣1）0+（）﹣2；
（2）3（x2+2）﹣3（x+1）（x﹣1）．
20．（8分）（1）解方程：x2+x﹣1＝0；
（2）解方程：．
21．（8分）如图，等边△AEF的顶点E，F在矩形ABCD的边BC，CD上，且∠CEF＝45°．求证：矩形ABCD是正方形．

22．（8分）已知不等式组．
（1）求不等式组的解集，并写出它的所有整数解；
（2）在不等式组的所有整数解中任取两个不同的整数相乘，请用画树状图或列表的方法求积为非负数的概率．
23．（8分）为了解某校学生的课余兴趣爱好情况，某调查小组设计了“阅读”、“打球”、“书法”和“舞蹈”四个选项，用随机抽样的方法调查了该校部分学生的课余兴趣爱好情况（每个学生必须选一项且只能选一项），并根据调查结果绘制了如图统计图．

根据统计图所提供的信息，解答下列问题：
（1）本次抽样调查中的学生人数是　 　；
（2）补全条形统计图；
（3）若该校共有1000名学生，请根据统计结果估计该校课余兴趣爱好为“打球”的学生人数．
24．（8分）按要求完成下列尺规作图（不写作图，保留作图痕迹）．

（1）如图①，点A、B、C是平行四边形ABCD的三个顶点，求作平行四边形ABCD；
（2）如图②，点O、P、Q分别是平行四边形EFGH三边EH、EF、FG的中点，求作平行四边形EFGH．
25．（8分）如图，已知AB是⊙O的直径，C是⊙O上的一点，D是AB上的一点，DE⊥AB于D，DE交BC于F，且EF＝EC．
（1）求证：EC是⊙O的切线；
（2）若BD＝4，BC＝8，圆的半径OB＝5，求切线EC的长．

26．（8分）某地新建的一个企业，每月将产生2020吨污水，为保护环境，该企业计划购置污水处理器，并在如下两个型号中选择：
污水处理器型号
A型
B型
处理污水能力（吨/月）
240
180
已知商家售出的2台A型、3台B型污水处理器的总价为44万元；售出的1台A型、4台B型污水处理器的总价为42万元．
（1）求每台A型、B型污水处理器的价格；
（2）为确保将每月产生的污水全部处理完，该企业决定购买上述A、B两种型号污水处理器共9台，那么．
①该企业有几种购买方案？
②哪种方案费用最低？最低费用是多少？
27．（10分）定义：长宽比为：1（n为正整数）的矩形称为矩形．下面，我们通过折叠的方式折出一个矩形，如图a所示．

操作1：将正方形ABEF沿过点A的直线折叠，使折叠后的点B落在对角线AE上的点G处，折痕为AH．
操作2：将FE沿过点G的直线折叠，使点F、点E分别落在边AF，BE上，折痕为CD．则四边形ABCD为矩形．
（1）证明：四边形ABCD为矩形；
（2）点M是边AB上一动点．
①如图b，O是对角线AC的中点，若点N在边BC上，OM⊥ON，连接MN．求tan∠OMN的值；
②若AM＝AD，点N在边BC上，当△DMN的周长最小时，求的值；
③连接CM，作BR⊥CM，垂足为R．若AB＝2，则DR的最小值＝　 　．
28．（10分）如图，抛物线y＝x2+bx+c与x轴分别交于A，B两点（点A在点B的左侧），与y轴交于点C，且OB＝OC＝3OA．
（1）求该抛物线的函数表达式；
（2）如图1，点D是该抛物线的顶点，点P（m，n）是第二象限内抛物线上的一个点，分别连接BD、BC、BP，当∠PBA＝2∠CBD时，求m的值；
（3）如图2，∠BAC的角平分线交y轴于点M，过M点的直线l与射线AB，AC分别于E，F，已知当直线l绕点M旋转时，+为定值，请直接写出该定值．


2021年江苏省无锡市新吴区中考数学二模试卷
参考答案与试题解析
一、选择题（本大题共10小题，每小题3分，共30分．）
1．（3分）2的倒数是（　　）
A．﹣2 B．2 C．﹣ D．
【分析】根据倒数的定义：乘积是1的两数互为倒数．一般地，a•＝1 （a≠0），就说a（a≠0）的倒数是 ．
【解答】解：2的倒数是，
故选：D．
2．（3分）下列图形中，是中心对称图形但不是轴对称图形的是（　　）
A． B． C． D．
【分析】根据轴对称图形与中心对称图形的概念求解．
【解答】解：A．不是轴对称图形，也不是中心对称图形．故本选项不合题意；
B．是中心对称图形但不是轴对称图形．故本选项符合题意；
C．是轴对称图形，也是中心对称图形．故本选项不合题意；
D．是轴对称图形，不是中心对称图形．故本选项不合题意．
故选：B．
3．（3分）下列运算正确的是（　　）
A．（a2）3＝a5 B．a4•a2＝a8 C．a6÷a3＝a2 D．（ab）3＝a3b3
【分析】根据同底数幂的除法法则，同底数幂的乘法的运算方法，以及幂的乘方与积的乘方的运算方法，逐项判定即可．
【解答】解：∵（a2）3＝a6，
∴选项A不符合题意；

∵a4•a2＝a6，
∴选项B不符合题意；

∵a6÷a3＝a3，
∴选项C不符合题意；

∵（ab）3＝a3b3，
∴选项D符合题意．
故选：D．
4．（3分）一个几何体的三视图如图所示，则这个几何体是（　　）

A．圆柱 B．圆锥 C．三棱柱 D．长方体
【分析】由常见几何体的三视图即可判断．
【解答】解：由三视图知这个几何体是三棱柱，
故选：C．
5．（3分）某鞋厂调查了商场一个月内不同尺码男鞋的销量，在平均数、中位数、众数和方差等数个统计量中，该鞋厂最关注的是（　　）
A．平均数 B．中位数 C．众数 D．方差
【分析】鞋厂最感兴趣的是各种鞋号的鞋的销售量，特别是销售量最多的即这组数据的众数．
【解答】解：由于众数是数据中出现最多的数，故鞋厂最感兴趣的销售量最多的鞋号即这组数据的众数．
故选：C．
6．（3分）如图，在半径为的圆形纸片中，剪一个圆心角为90°的最大扇形（阴影部分），则这个扇形的面积为（　　）

A．π B． C．2π D．
【分析】由勾股定理求扇形的半径，再根据扇形面积公式求值．
【解答】解：连接BC，
由∠BAC＝90°得BC为⊙O的直径，
∴BC＝2，
在Rt△ABC中，由勾股定理可得：AB＝AC＝2，
∴S扇形ABC＝＝π，
故选：A．

7．（3分）如图，A为反比例函数y＝（其中x＞0）图象上的一点，在x轴正半轴上有一点B，OB＝6．连接OA，AB，且OA＝AB．过点B作BC⊥OB，交反比例函数y＝（其中x＞0）的图象于点C，连接OC交AB于点D，S△OBC＝6，则AB的长度为（　　）

A．4 B．5 C．5 D．5
【分析】过点A作AH⊥x轴于点H，先由△OBC的面积为6得△OAH的面积，然后结合OA＝AB得到AH的长度，最后求得AB的长度．
【解答】解：过点A作AH⊥x轴于点H，则S△AOH＝|k|，
∵BC⊥x轴，
∴S△OBC＝|k|＝6，
∴S△AOH＝AH•OH＝6，
∵OA＝AB，AH⊥OB，OB＝6，
∴OH＝HB＝3，
∴×3×AH＝6，
∴AH＝4，
∴AB＝＝5．
故选：C．

8．（3分）如图，已知线段AB，分别以A，B为圆心，大于AB同样长为半径画弧，两弧交于点C，D，连接AC，AD，BC，BD，CD，则下列说法错误的是（　　）

A．AB平分∠CAD B．CD平分∠ACB C．AB⊥CD D．AB＝CD
【分析】根据作图判断出四边形ACBD是菱形，再根据菱形的性质：菱形的对角线平分一组对角、菱形的对角线互相垂直平分可得出答案．
【解答】解：由作图知AC＝AD＝BC＝BD，
∴四边形ACBD是菱形，
∴AB平分∠CAD、CD平分∠ACB、AB⊥CD，
不能判断AB＝CD，
故选：D．
9．（3分）点P（a，b）在以y轴为对称轴的二次函数y＝x2+mx+5的图象上，则2a﹣b的最大值等于（　　）
A．4 B．﹣4 C．﹣4.5 D．4.5
【分析】根据二次函数以y轴为对称轴可得y＝x2+5，把点P（a，b）代入，b＝a2+5，所以2a﹣b＝﹣a2+2a﹣5，最后求关于a的二次函数的最值即可．
【解答】解：点P（a，b）在以y轴为对称轴的二次函数y＝x2+mx+5的图象上，
∴m＝0，b＝a2+5，
∴2a﹣b＝﹣a2+2a﹣5，
令s＝﹣a2+2a﹣5，
当a＝1时，s取得最大值为﹣4，
故2a﹣b的最大值等于﹣4，
故选：B．
10．（3分）如图，C为线段AB上一点，在线段AB的同侧分别作等边△ACD、△BCE，连接AE、BD相交于F，连接CF．若S△DEF＝8，则CF的长为（　　）

A．4 B．3 C．3 D．4
【分析】如图，作EH⊥BD于H．首先证明∠DFA＝∠AFC＝∠CFB＝60°，再证明△DFC∽△CFE，推出，推出CF2＝DF•EF，由S△DEF＝•DF•EF•sin60°＝，推出DF•EF＝32，可得CF2＝32，由此即可解决问题．
【解答】解：如图，作EH⊥BD于H，设AE与DC交于点O，

∵△ADC，△EBC都是等边三角形，
∴CA＝CD，CE＝CB，∠ACD＝∠ECB＝60°，
∴∠ACE＝∠DCB，
在△ACE和△DCB中，
，
∴△ACE≌△DCB（SAS），
∴∠CAE＝∠CDB，
∵∠AOC＝∠DOF，
∴∠DFO＝∠OCA＝60°，
∴△DOF∽△AOC，
∴，
∴，
∵∠AOD＝∠FOC，
∴△DOA∽△FOC，
∴∠ADO＝∠OFC＝60°，∠DCF＝∠DAF，
∴∠CFB＝60°，
∴∠DFC＝∠EFC＝120°，
∵∠ECB＝∠DAC＝60°，
∴AD∥CE，
∴∠DAF＝∠FEC，
∴∠DCF＝∠FEC，
∴△DFC∽△CFE，
∴，
∴CF2＝DF•EF，
∵S△DEF＝•DF•EF•sin60°＝，
∴DF•EF＝32，
∴CF2＝32，
∵CF＞0，
∴CF＝4．
故选：A．
二、填空题（本大题共8小题，每小题3分，共16分．不需写出解答过程，只需把答案填写在答卷纸的相应位置处）
11．（3分）如果分式有意义，那么实数x的取值范围是　x≠2　．
【分析】根据分式有意义的条件可得x﹣2≠0，再解即可．
【解答】解：由题意得：x﹣2≠0，
解得：x≠2，
故答案为：x≠2．
12．（3分）地球到太阳的距离为150000000km，将150000000km用科学记数法表示为　1.5×108　km．
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于1时，n是正数；当原数的绝对值小于1时，n是负数．
【解答】解：150 000 000＝1.5×108km．
13．（3分）正十边形一个内角度数为　144°　．
【分析】利用正十边形的外角和是360度，并且每个外角都相等，即可求出每个外角的度数；再根据内角与外角的关系可求出正十边形的每个内角的度数；
【解答】解：∵一个十边形的每个外角都相等，
∴十边形的一个外角为360÷10＝36°．
∴每个内角的度数为 180°﹣36°＝144°；
故答案为：144°．
14．（3分）若一组数据3，4，5，x，6，7的平均数是5，则x的值是　5　．
【分析】根据平均数的定义计算即可．
【解答】解：根据题意知（3+4+5+x+6+7）÷6＝5，
解得：x＝5，
故答案为：5．
15．（3分）如图是某商场营业大厅自动扶梯示意图．自动扶梯AB的倾斜角为30°，在自动扶梯下方地面C处测得扶梯顶端B的仰角为60°，A、C之间的距离为4m．则自动扶梯的垂直高度BD＝　　m．（结果保留根号）

【分析】根据等腰三角形的性质和三角形的外角的性质得到BC＝AC＝4m，根据三角函数的定义即可得到结论．
【解答】解：∵∠BCD＝∠BAC+∠ABC，∠BAC＝30°，∠BCD＝60°，
∴∠ABC＝∠BCD﹣∠BAC＝30°，
∴∠BAC＝∠ABC，
∴BC＝AC＝4m，
在Rt△BDC中，sin∠BCD＝，
∴sin60°＝＝，
∴BD＝2m，
故答案为：2．
16．（3分）如图，菱形ABOC的边AB，AC分别与⊙O相切于点D，E．若点D是AB的中点，则∠DOE＝　60　°．

【分析】连接OA，根据菱形的性质得到△AOB是等边三角形，根据切线的性质求出∠AOD，同理计算即可．
【解答】解：连接OA，
∵四边形ABOC是菱形，
∴BA＝BO，
∵AB与⊙O相切于点D，
∴OD⊥AB，
∵点D是AB的中点，
∴直线OD是线段AB的垂直平分线，
∴OA＝OB，
∴△AOB是等边三角形，
∵AB与⊙O相切于点D，
∴OD⊥AB，
∴∠AOD＝∠AOB＝30°，
同理，∠AOE＝30°，
∴∠DOE＝∠AOD+∠AOE＝60°，
故答案为：60．

17．（3分）把一张宽为2cm的长方形纸片ABCD折叠成如图所示的阴影图案，顶点A，D互相重合，中间空白部分是以E为直角顶点，腰长为4cm的等腰直角三角形，则纸片的长AD为 　16+8　cm．

【分析】过点M作MH⊥A'R于点H，过点N作NJ⊥A'W于J，计算求出AR，RM，MN，NW，WD，即可得出结论．
【解答】解：过点M作MH⊥A'R于点H，过点N作NJ⊥A'W于J，如图所示，
由题意△EMN是等腰直角三角形，得△RHM是等腰直角三角形，EM＝EN＝4，
∴MN＝4（cm），
∵四边形EMHK是矩形，
∴EK＝A'K＝MH＝2（cm），KH＝EM＝4（cm），
∵△RMH是等腰直角三角形，
∴RH＝HM＝2（cm），
∴RM＝2（cm），
同理可得，NW＝2（cm），
由折叠可得，AR＝A'R＝A'W＝WD＝RH+HK+KA'＝2+4+2＝8（cm），
∴AD＝AR+RM+MN+NW+WD＝8+2+4+2+8＝16+8（cm），
故答案为：16+8．

18．（3分）如图，在平面直角坐标系中，A（3，0），B（0，4），M为AB边上的一动点，N（0，1），连接MN，将△ABO绕点O逆时针旋转一周，则MN的取值范围为 　≤MN≤5　．

【分析】如图，过点O作OF⊥AB于点F．利用面积法求出OF＝，以O为圆心，OF，OB为半径作圆，则点M的轨迹形成的图形是圆环（包括两个圆），求出MN的最大值和最小值，可得结论．
【解答】解：如图，过点O作OF⊥AB于点F．

∵A（3，0），B（0，4），
∴OA＝3，OB＝4，
∴AB＝＝＝5，
∵S△AOB＝•OA•OB＝•AB•OF，
∴OF＝，
以O为圆心，OF，OB为半径作圆，则点M的轨迹形成的图形是圆环（包括两个圆），
∴NM的最大值＝1+4＝5，NM的最小值＝﹣1＝，
∴≤MN≤5，
故答案为：≤MN≤5，
三、解答题（本大题共10小题，共84分．请在答卷相应的区域内作答，解答时应写出文字说明、证明过程或演算步骤．）
19．（8分）计算：
（1）2sin45°﹣（﹣1）0+（）﹣2；
（2）3（x2+2）﹣3（x+1）（x﹣1）．
【分析】（1）求三角函数值、0次幂、负整数次幂，最后求值；
（2）先去括号，再用平方差公式计算．
【解答】（1）解：原式＝﹣1+4
＝+3；
（2）解：原式＝3x2+6﹣3x2+3
＝9．
20．（8分）（1）解方程：x2+x﹣1＝0；
（2）解方程：．
【分析】（1）利用公式法解出方程；
（2）先把分式方程化为整式方程，解整式方程求出x，检验得到答案．
【解答】解：（1）a＝1，b＝1，c＝﹣1，
△＝1﹣4×1×（﹣1）＝5＞0，
方程有两个不相等的实数根，x＝＝，
即x1＝，x2＝；
（2）方程两边同乘（x+3）（x﹣3），得（x﹣3）2＝2（x+3）（x﹣3）﹣x（x+3）
整理得：3x＝27，
解得：x＝9，
检验，当x＝9时，（x+3）（x﹣3）≠0，
所以原方程的解为x＝9．
21．（8分）如图，等边△AEF的顶点E，F在矩形ABCD的边BC，CD上，且∠CEF＝45°．求证：矩形ABCD是正方形．

【分析】先判断出AE＝AF，∠AEF＝∠AFE＝60°，进而求出∠AFD＝∠AEB＝75°，进而判断出△AEB≌△AFD，即可得出结论．
【解答】解：∵四边形ABCD是矩形，
∴∠B＝∠D＝∠C＝90°，
∵△AEF是等边三角形，
∴AE＝AF，∠AEF＝∠AFE＝60°，
∵∠CEF＝45°，
∴∠CFE＝∠CEF＝45°，
∴∠AFD＝∠AEB＝180°﹣45°﹣60°＝75°，
∴△AEB≌△AFD（AAS），
∴AB＝AD，
∴矩形ABCD是正方形．
22．（8分）已知不等式组．
（1）求不等式组的解集，并写出它的所有整数解；
（2）在不等式组的所有整数解中任取两个不同的整数相乘，请用画树状图或列表的方法求积为非负数的概率．
【分析】（1）分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集，继而得出答案；
（2）画树状图列出所有等可能结果，从中找到符合条件的结果数，再根据概率公式求解即可．
【解答】解：（1），
由①得：x＞﹣2，由②得：x≤2，
∴不等式组的解集为：﹣2＜x≤2，
∴它的所有整数解为：﹣1，0，1，2；

（2）画树状图得：

∵共有12种等可能的结果，积为非负数的有8种情况，
∴积为非负数数的概率为＝．
23．（8分）为了解某校学生的课余兴趣爱好情况，某调查小组设计了“阅读”、“打球”、“书法”和“舞蹈”四个选项，用随机抽样的方法调查了该校部分学生的课余兴趣爱好情况（每个学生必须选一项且只能选一项），并根据调查结果绘制了如图统计图．

根据统计图所提供的信息，解答下列问题：
（1）本次抽样调查中的学生人数是　100　；
（2）补全条形统计图；
（3）若该校共有1000名学生，请根据统计结果估计该校课余兴趣爱好为“打球”的学生人数．
【分析】（1）用选“阅读”的人数除以它所占的百分比即可得到调查的总人数；
（2）先计算出选“舞蹈”的人数，再计算出选“打球”的人数，然后补全条形统计图；
（3）用2000乘以样本中选“打球”的人数所占的百分比可估计该校课余兴趣爱好为“打球”的学生人数．
【解答】解：（1）本次抽样调查中的学生人数是：30÷30%＝100（人），
即本次抽样调查中的学生人数是100人，
故答案为：100；
（2）选”舞蹈”的人数为100×10%＝10（人），
选“打球”的人数为100﹣30﹣10﹣20＝40（人），
补全条形统计图为：
40，10补全图形并标注数字；
（3）1000×＝400（人），
所以估计该校课余兴趣爱好为“打球”的学生人数为400人．
24．（8分）按要求完成下列尺规作图（不写作图，保留作图痕迹）．

（1）如图①，点A、B、C是平行四边形ABCD的三个顶点，求作平行四边形ABCD；
（2）如图②，点O、P、Q分别是平行四边形EFGH三边EH、EF、FG的中点，求作平行四边形EFGH．
【分析】（1）分别以A、C点为圆心，BC和AB为半径画弧相交于点D，则利用平行四边形的判定方法可判断四边形ABCD满足条件；
（2）利用（1）中的方法先以O、P、Q三点画平行四边形OPQK，对角线相交于点O，然后再分别画平行四边形可得到满足条件的四边形EFGH．
【解答】解：（1）如图①，四边形ABCD即为所求；
（2）如图②，四边形EFGH即为所求．

25．（8分）如图，已知AB是⊙O的直径，C是⊙O上的一点，D是AB上的一点，DE⊥AB于D，DE交BC于F，且EF＝EC．
（1）求证：EC是⊙O的切线；
（2）若BD＝4，BC＝8，圆的半径OB＝5，求切线EC的长．

【分析】（1）连接OC，由等腰三角形的性质和直角三角形的性质可得∠OCB+∠ECF＝90°，可证EC是⊙O的切线；
（2）由勾股定理可求AC＝6，由锐角三角函数可求BF＝5，可求CF＝3，通过证明△OAC∽△ECF，可得，可求解．
【解答】解：（1）连接OC，

∵OC＝OB，
∴∠OBC＝∠OCB，
∵DE⊥AB，
∴∠OBC+∠DFB＝90°，
∵EF＝EC，
∴∠ECF＝∠EFC＝∠DFB，
∴∠OCB+∠ECF＝90°，
即∠ECO＝90°，
∴OC⊥CE，
∴EC是⊙O的切线；
（2）∵AB是⊙O的直径，
∴∠ACB＝90°，
∵OB＝5，
∴AB＝10，
∴AC＝＝＝6，
∵cos∠ABC＝，
∴，
∴BF＝5，
∴CF＝BC﹣BF＝3，
∵∠ABC+∠A＝90°，∠ABC+∠BFD＝90°，
∴∠BFD＝∠A，
∴∠A＝∠BFD＝∠ECF＝∠EFC，
∵OA＝OC，
∴∠OCA＝∠A＝∠BFD＝∠ECF＝∠EFC，
∴△OAC∽△ECF，
∴，
∴EC＝＝＝．
26．（8分）某地新建的一个企业，每月将产生2020吨污水，为保护环境，该企业计划购置污水处理器，并在如下两个型号中选择：
污水处理器型号
A型
B型
处理污水能力（吨/月）
240
180
已知商家售出的2台A型、3台B型污水处理器的总价为44万元；售出的1台A型、4台B型污水处理器的总价为42万元．
（1）求每台A型、B型污水处理器的价格；
（2）为确保将每月产生的污水全部处理完，该企业决定购买上述A、B两种型号污水处理器共9台，那么．
①该企业有几种购买方案？
②哪种方案费用最低？最低费用是多少？
【分析】（1）设每台A型污水处理器x万元，每台B型污水处理器y万元，根据“商家售出的2台A型、3台B型污水处理器的总价为44万元；售出的1台A型、4台B型污水处理器的总价为42万元”，即可得出关于x，y的二元一次方程组，解之即可得出结论；
（2）①设购买A型污水处理器m台，则购买B型污水处理器（9﹣m）台，根据每个月至少处理污水2020吨，即可得出关于m的一元一次不等式，结合m，（9﹣m）均为正整数，即可得出各购买方案；
②根据总价＝单价×数量，可分别求出各购买方案所需费用，比较后即可得出结论．
【解答】解：（1）设每台A型污水处理器x万元，每台B型污水处理器y万元，
依题意，得：，
解得：．
答：每台A型污水处理器10万元、每台B型污水处理器8万元．
（2）①设购买A型污水处理器m台，则购买B型污水处理器（9﹣m）台，
依题意，得：240m+180（9﹣m）≥2020，
解得：m≥6，
∵m，（9﹣m）均为正整数，
∴m可以为7，8，
∴共有2种购买方案，方案1：购进A型污水处理器7台，B型污水处理器2台；方案2：购进A型污水处理器8台，B型污水处理器1台．
②方案1所需费用为10×7+8×2＝86（万元）；
方案2所需费用为10×8+8×1＝88（万元）．
∵86＜88，
∴方案1购进A型污水处理器7台，B型污水处理器2台费用最低，最低费用为86万元．
27．（10分）定义：长宽比为：1（n为正整数）的矩形称为矩形．下面，我们通过折叠的方式折出一个矩形，如图a所示．

操作1：将正方形ABEF沿过点A的直线折叠，使折叠后的点B落在对角线AE上的点G处，折痕为AH．
操作2：将FE沿过点G的直线折叠，使点F、点E分别落在边AF，BE上，折痕为CD．则四边形ABCD为矩形．
（1）证明：四边形ABCD为矩形；
（2）点M是边AB上一动点．
①如图b，O是对角线AC的中点，若点N在边BC上，OM⊥ON，连接MN．求tan∠OMN的值；
②若AM＝AD，点N在边BC上，当△DMN的周长最小时，求的值；
③连接CM，作BR⊥CM，垂足为R．若AB＝2，则DR的最小值＝　2　．
【分析】（1）先判断出∠DAG＝45°，进而判断出四边形ABCD是矩形，再求出AB：AD的值，即可得出结论；
（2）①如图b，先判断出四边形BQOP是矩形，进而得出，，再判断出Rt△QON∽Rt△POM，进而判断出＝．，即可得出结论；
②作M关于直线BC对称的点P，则△DMN的周长最小，判断出，得出AB＝CD＝a．进而得出BP＝BM＝AB﹣AM＝（﹣1）a．即可得出结论；
③先求出BC＝AD＝2，再判断出点R是BC为直径的圆上，即可得出结论．
【解答】证明：（1）设正方形ABEF的边长为a，
∵AE是正方形ABEF的对角线，
∴∠DAG＝45°，
由折叠性质可知AG＝AB＝a，∠FDC＝∠ADC＝90°，
则四边形ABCD为矩形，
∴△ADG是等腰直角三角形．
∴AD＝DG＝，
∴AB：AD＝a：＝：1．
∴四边形ABCD为矩形；

（2）①解：如图b，作OP⊥AB，OQ⊥BC，垂足分别为P，Q．
∵四边形ABCD是矩形，∠B＝90°，
∴四边形BQOP是矩形．
∴∠POQ＝90°，OP∥BC，OQ∥AB．
∴，．
∵O为AC中点，
∴OP＝BC，OQ＝AB．
∵∠MON＝90°，
∴∠QON＝∠POM．
∴Rt△QON∽Rt△POM．
∴＝．
∴tan∠OMN＝．
②解：如图c，作M关于直线BC对称的点P，连接DP交BC于点N，连接MN．
则△DMN的周长最小，
∵DC∥AP，
∴，
设AM＝AD＝a，则AB＝CD＝a．
∴BP＝BM＝AB﹣AM＝（﹣1）a．
∴＝＝2+，
③如备用图，
∵四边形ABCD为矩形，AB＝2，
∴BC＝AD＝2，
∵BR⊥CM，
∴点R在以BC为直径的圆上，记BC的中点为I，
∴CI＝BC＝1，
∴DR最小＝﹣1＝2
故答案为：2


28．（10分）如图，抛物线y＝x2+bx+c与x轴分别交于A，B两点（点A在点B的左侧），与y轴交于点C，且OB＝OC＝3OA．
（1）求该抛物线的函数表达式；
（2）如图1，点D是该抛物线的顶点，点P（m，n）是第二象限内抛物线上的一个点，分别连接BD、BC、BP，当∠PBA＝2∠CBD时，求m的值；
（3）如图2，∠BAC的角平分线交y轴于点M，过M点的直线l与射线AB，AC分别于E，F，已知当直线l绕点M旋转时，+为定值，请直接写出该定值．

【分析】（1）设OA＝t（t＞0），则OB＝OC＝3t，可得该抛物线的对称轴为直线x＝t，有b＝﹣2t，将A（﹣t，0），C （0，﹣3t）代入即可求出该抛物线的解析式为y＝x2﹣2x﹣3；
（2）取BC中点G，作GH⊥BD于H，连接CH，过C作CM⊥BD于M，过P作PN⊥x轴于N，由抛物线顶点D坐标为（1，﹣4），B（3，0），C（0，﹣3），可得∠BCD＝90°，GH∥CD，从而H为BD中点，CH＝BH＝BD＝，由面积法得CM＝＝，故tan∠CHM＝，即知tan∠PBA＝，即＝，设P（m，m2﹣2m﹣3），得＝，即可得m的值为﹣；
（3）过M作MG∥x轴交AC于G，过F作FT∥x轴交AM于T，过C作CQ∥x轴交AM于Q，由MG∥FT∥CQ∥OA，得△COA∽△CMG，△ACQ∽AGM，有＝，＝，故+＝+＝1，即得+＝，根据AM平分∠BAC，可得AC＝CQ，从而+＝，同理可得+＝，又A（﹣1，0），C（0，﹣3），即得+＝＝+＝．
【解答】解：（1）设OA＝t（t＞0），
∵OB＝OC＝3OA，
∴OB＝OC＝3t，
∴A（﹣t，0），B（3t，0），C （0，﹣3t），
∴该抛物线的对称轴为直线x＝﹣＝＝t，
∴b＝﹣2t①，
将A（﹣t，0），C （0，﹣3t），代入得：
，
①②③联立解得：，（t＝0已舍去），
∴该抛物线的解析式为y＝x2﹣2x﹣3；
（2）取BC中点G，作GH⊥BD于H，连接CH，过C作CM⊥BD于M，过P作PN⊥x轴于N，如图：

由y＝x2﹣2x﹣3得抛物线顶点D坐标为（1，﹣4），
而B（3，0），C（0，﹣3），
∴BC＝3，CD＝，BD＝2，
∴BC2+CD2＝20，BD2＝20，
∴BC2+CD2＝BD2，
∴∠BCD＝90°，
∵GH⊥BD，
∴GH∥CD，
∵G为BC中点，
∴H为BD中点，
∴CH＝BH＝BD＝，
∴∠CHM＝2∠CBD＝∠PBA，
∵CM＝＝，
∴MH＝＝，
∴tan∠CHM＝，
∴tan∠PBA＝，即＝，
设P（m，m2﹣2m﹣3），则＝
解得m1＝3（与B重合，舍去）或m2＝﹣，
∴m的值为﹣；
（3）过M作MG∥x轴交AC于G，过F作FT∥x轴交AM于T，过C作CQ∥x轴交AM于Q，如图：

∵MG∥x轴，FT∥x轴，CQ∥x轴，
∴MG∥FT∥CQ∥OA，
∴△COA∽△CMG，△ACQ∽AGM，
∴＝，＝，
∴+＝+＝1，
∴+＝，
∵AM平分∠BAC，
∴∠CAM＝∠BAM＝∠AQC，
∴AC＝CQ，
∴+＝，
同理可得+＝，
由（1）可知：A（﹣1，0），C（0，﹣3），
∴AC＝，
∴+＝＝+＝+＝．