人教版九年级上册22.3 实际问题与二次函数优秀一课一练

22.3.7 二次函数与几何综合：面积最值  同步练习

一．解答题（共11题）。

1．（2020·黑龙江讷河·月考）如图，抛物线与轴交于， 两点，点在点 的左边，与轴交于点，点是抛物线的顶点，且，．

（1）求抛物线的解析式；

（2）点是直线下方的抛物线上一动点，不与点，重合，过点 作 轴的垂线交 于点，求面积的最大值及此时点坐标；

2．（2019·江苏东台市实验中学期中）如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于A、B两点，其中A点坐标为（－1，0），点B（5，0），D（1，8）在抛物线上，M为抛物线的顶点．

（1）求抛物线的解析式；

（2）求△MCB的面积．

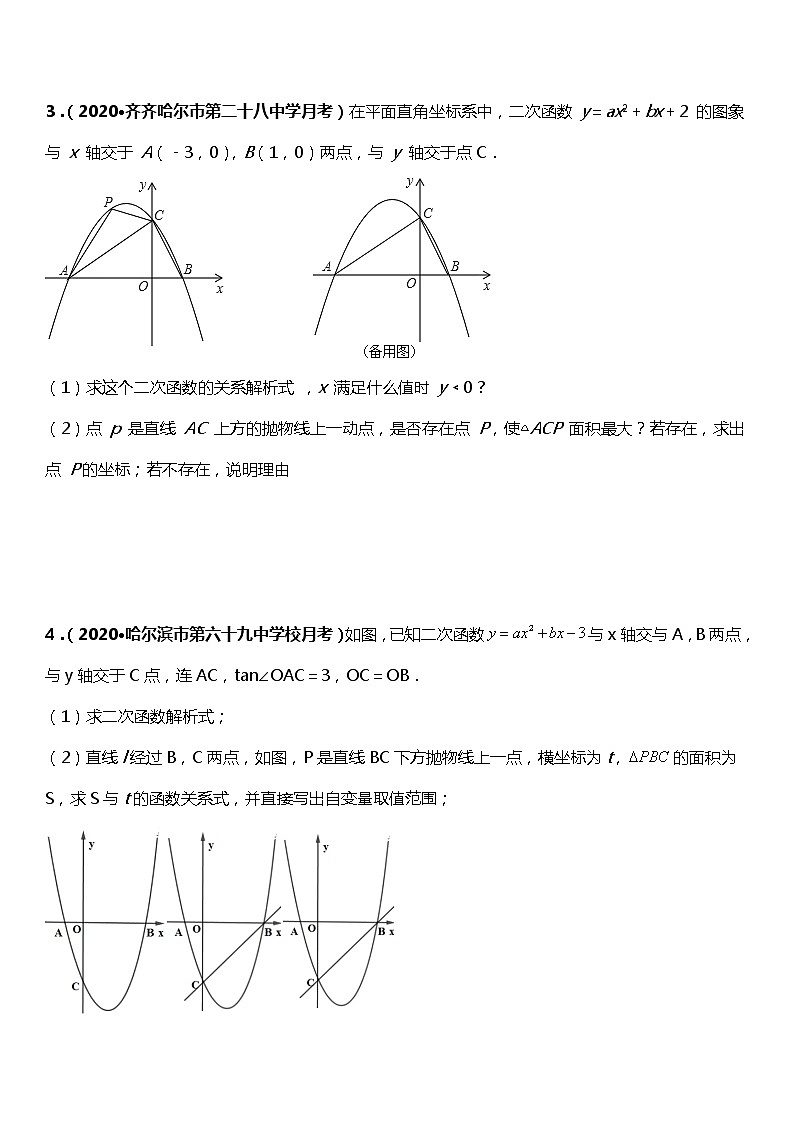
3．（2020·齐齐哈尔市第二十八中学月考）在平面直角坐标系中，二次函数 y＝ax2＋bx＋2 的图象与 x 轴交于 A（﹣3，0），B（1，0）两点，与 y 轴交于点C．

（1）求这个二次函数的关系解析式 ，x 满足什么值时 y﹤0 ?

（2）点 p 是直线 AC 上方的抛物线上一动点，是否存在点 P，使△ACP 面积最大？若存在，求出点 P的坐标；若不存在，说明理由

4．（2020·哈尔滨市第六十九中学校月考）如图，已知二次函数与x轴交与A，B两点，与y轴交于C点，连AC，tan∠OAC＝3，OC＝OB．

（1）求二次函数解析式；

（2）直线l经过B，C两点，如图，P是直线BC下方抛物线上一点，横坐标为t，的面积为S，求S与t的函数关系式，并直接写出自变量取值范围；

5．（2020·北京师范大学厦门海沧附属学校月考）如图，直线l：与x轴、y轴分别相交于A、B两点，抛物线经过点B．

(1)求该抛物线的函数表达式：

(2)已知点M是抛物线上的一个动点，并且点M在第一象限内，连接AM、BM，设点M的横坐标为m，△ABM的面积为S，求S与m的函数表达式，并求出S的最大值．

6．（2020·海门市包场初级中学月考）如图，抛物线y=ax2+bx+c经过点A（﹣1，0），C（0，3），抛物线的顶点在直线上．

（1）求抛物线的解析式；

（2）若点P为第一象限内抛物线上的一点，设△PBC的面积为S，求S的最大值并求出此时点P的坐标；

7．（2020·民勤县第六中学三模）如图，抛物线y=﹣x2+bx+c经过点A，B，C，已知点A（﹣1，0），点C（0，3）．

（1）求抛物线的表达式；

（2）P为线段BC上一点，过点P作y轴的平行线，交抛物线于点D，当△BDC的面积最大时，求点P的坐标；

8．（2020·河南卧龙·期末）如图，抛物线y＝ax2+bx+3（a≠0）的对称轴为直线x＝﹣1，抛物线交x轴于A、C两点，与直线y＝x﹣1交于A、B两点，直线AB与抛物线的对称轴交于点E．

（1）求抛物线的解析式．

（2）点P在直线AB上方的抛物线上运动，若△ABP的面积最大，求此时点P的坐标．

9．（2020·广东三模）如图，抛物线与轴相交于两点（点位于点的左侧），与轴相交于点，是抛物线的顶点，直线是抛物线的对称轴，且点的坐标为．

（1）求抛物线的解析式．

（2）已知为线段上一个动点，过点作轴于点．若的面积为．

①求与之间的函数关系式，并写出自变量的取值范围；

②当取得最值时，求点的坐标．

10．（2020·山东德州·二模）如图，抛物线与x轴交于点，点，与y轴交于点C，且过点．点P、Q是抛物线上的动点．

(1)求抛物线的解析式；

(2)当点P在直线OD下方时，求面积的最大值．

11．（2020·海口市第九中学其他）如图，直线y＝﹣x+3与x轴、y轴分别交于B、C两点，经过B、C两点的抛物线y＝x2+bx+c与x轴的另一个交点为A，顶点为P．

（1）求该抛物线的解析式；

（2）当0＜x＜3时，在抛物线上求一点E，使△CBE的面积有最大值；

答案解析

1．（2020·黑龙江讷河·月考）如图，抛物线与轴交于， 两点，点在点 的左边，与轴交于点，点是抛物线的顶点，且，．

（1）求抛物线的解析式；

（2）点是直线下方的抛物线上一动点，不与点，重合，过点 作 轴的垂线交 于点，求面积的最大值及此时点坐标；

【答案】（1）y＝x2＋2x－6；（2）S△ACP有最大值，点P的坐标是（－3，－）；

【分析】

（1）设抛物线的解析式是y＝a（x＋2）2－8，把A（－6，0）代入即可求出解析式；

（2）先求出点C（0，－6），设点P（m，m2＋2m－6），设直线AC的解析式是y＝kx＋b，解得直线AC的解析式是y＝－x－6，得到E（m，－m－6），PE＝－m2－3m，利用S△ACP＝S△AEP＋S△CEP，即可得到答案；

【详解】

（1）设抛物线的解析式是y＝a（x＋2）2－8，把A（－6，0）代入得a（－6＋2）2－8＝0，解得a＝，

∴y＝（x＋2）2－8＝x2＋2x－6；

（2）解：当x＝0时，y＝－6，∴C（0，－6），

设点P（m，m2＋2m－6），

设直线AC的解析式是y＝kx＋b，

把A（－6，0），C（0，－6）代入得

，解得

∴直线AC的解析式是y＝－x－6，

∵PE⊥x轴交AC于E，

∴E（m，－m－6），

∴PE＝－m－6－（m2＋2m－6）＝－m2－3m（－6＜m＜0），

∵S△ACP＝S△AEP＋S△CEP＝=,

∴当m＝－3时，S△ACP有最大值，最大值为，

此时点P的坐标是（－3，－）；

【点睛】

此题是二次函数的综合题，考查了待定系数法求函数解析式，函数与几何图形面积问题，勾股定理，直角三角形与函数图象的结合问题，正确理解题意根据题意画出图形解答是关键.

2．（2019·江苏东台市实验中学期中）如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于A、B两点，其中A点坐标为（－1，0），点B（5，0），D（1，8）在抛物线上，M为抛物线的顶点．

（1）求抛物线的解析式；

（2）求△MCB的面积．

【答案】（1）y=-x2+4x+5；（2）△MCB的面积为15．

【解析】

【分析】

（1）由A、C、D三点在抛物线上，根据待定系数法即可求出抛物线的解析式；
（2）过点M作MN∥y轴交BC轴于点N，则△MCB的面积=△MCN的面积+△MNB的面积=MN•OB．

【详解】

解：（1）∵A（-1，0），C（0，5），D（1，8）三点在抛物线y=ax2+bx+c上，
∴，
解方程组，得，
故抛物线的解析式为y=-x2+4x+5；
故答案是：y=-x2+4x+5；
（2）过点M作MN∥y轴交BC轴于点N，则△MCB的面积=△MCN的面积+△MNB的面积=MN•OB．

∵y=-x2+4x+5=-（x-5）（x+1）=-（x-2）2+9，
∴M（2，9），B（5，0），
由B、C两点的坐标易求得直线BC的解析式为：y=-x+5，
当x=2时，y=-2+5=3，则N（2，3），
则MN=9-3=6，
则S△MCB=×6×5=15．
故答案是：15．

【点睛】

本题考查了解二次函数综合题的方法：先运用待定系数法求出二次函数的解析式，确定各特殊点的坐标，得到有关线段的长，求出三角形的面积．

3．（2020·齐齐哈尔市第二十八中学月考）在平面直角坐标系中，二次函数 y＝ax2＋bx＋2 的图象与 x 轴交于 A（﹣3，0），B（1，0）两点，与 y 轴交于点C．

（1）求这个二次函数的关系解析式 ，x 满足什么值时 y﹤0 ?

（2）点 p 是直线 AC 上方的抛物线上一动点，是否存在点 P，使△ACP 面积最大？若存在，求出点 P的坐标；若不存在，说明理由

【答案】（1）， 或；（2）P；

【解析】

【分析】

（1）将点A（﹣3，0），B（1，0）带入y＝ax2＋bx＋2得到二元一次方程组，解得即可得出函数解析式；又从图像可以看出x 满足什么值时 y﹤0；

（2）设出P点坐标，利用割补法将△ACP 面积转化为，带入各个三角形面积算法可得出与m之间的函数关系，分析即可得出面积的最大值；

【详解】

解：（1）将A（﹣3，0），B（1，0）两点带入y＝ax2＋bx＋2可得：

解得：

∴二次函数解析式为.

由图像可知，当或时y﹤0；

综上：二次函数解析式为，当或时y﹤0；

（2）设点P坐标为，如图连接PO，作PM⊥x轴于M，PN⊥y轴于N.

PM=，PN=，AO=3.

当时，，所以OC=2

，

∵

∴函数有最大值，

当时，有最大值，

此时；

所以存在点，使△ACP 面积最大.

【点睛】

本题考查二次函数与几何综合题目，涉及到用待定系数法求二次函数解析式，通过函数图像得出关于二次函数不等式的解集，平面直角坐标系中三角形面积的计算通常利用割补法，并且将所要求得点的坐标设出来，得出相关方程.

4．（2020·哈尔滨市第六十九中学校月考）如图，已知二次函数与x轴交与A，B两点，与y轴交于C点，连AC，tan∠OAC＝3，OC＝OB．

（1）求二次函数解析式；

（2）直线l经过B，C两点，如图，P是直线BC下方抛物线上一点，横坐标为t，的面积为S，求S与t的函数关系式，并直接写出自变量取值范围；

【答案】（1）

（2）

【解析】

【分析】

（1）根据所给解析式可求出点C的坐标，得到OC的长，则OB的长也知道了，得到点B的坐标，再根据，求出OA的长，得到点A的坐标，将点A和点B的坐标代入解析式，求出系数a和b，得到解析式

（2）过点P作y轴的平行线，交BC于点Q，先求出直线BC的解析式，设，则，的面积用水平宽乘铅垂高除以2的方法来表示；

【详解】

解：（1）令，则，

∴，

∴，则，

∵，

∴，即，则，

将点A和点B的坐标代入解析式，得，解得，

∴二次函数解析式为：；

（2）如图，过点P作y轴的平行线，交BC于点Q，

根据点B和点C的坐标，用待定系数法求出直线BC的解析式：，

设，则，

，

；

【点睛】

本题考查二次函数综合，解题的关键是掌握二次函数解析式的求法，平面直角坐标系中三角形面积的表示方法．

5．（2020·北京师范大学厦门海沧附属学校月考）如图，直线l：与x轴、y轴分别相交于A、B两点，抛物线经过点B．

(1)求该抛物线的函数表达式：

(2)已知点M是抛物线上的一个动点，并且点M在第一象限内，连接AM、BM，设点M的横坐标为m，△ABM的面积为S，求S与m的函数表达式，并求出S的最大值．

【答案】（1）；（2）;当时，取得最大值．

【解析】

【分析】

（1）根据题意先求出点B的坐标，然后代入二次函数解析式求解即可；

（2）由题意可求点A坐标，连接，由题意知，点的坐标为，则有，然后根据割补法求面积即可．

【详解】

解：（1）把代入得，

∴．

把代入，

得，∴．

∴抛物线的解析式为；

（2）令，则，解得或3，

∴抛物线与轴的交点横坐标分别为和3．

∵点在抛物线上，且在第一象限内，

∴．

将代入，得，解得，

∴．

如解图，连接，由题意知，点的坐标为，

则

，

∵，且，

∴当时，取得最大值．

【点睛】

本题主要考查二次函数的综合，熟练掌握二次函数的性质是解题的关键．

6．（2020·海门市包场初级中学月考）如图，抛物线y=ax2+bx+c经过点A（﹣1，0），C（0，3），抛物线的顶点在直线上．

（1）求抛物线的解析式；

（2）若点P为第一象限内抛物线上的一点，设△PBC的面积为S，求S的最大值并求出此时点P的坐标；

【答案】（1）；（2）；

【解析】

【分析】

（1）利用待定系数法即可求出结论；

（2）利用抛物线的对称性求出点B的坐标，设点P（x，），过点P作PQ⊥x轴，交BC于点Q，利用待定系数法即可求出直线BC的解析式，从而求出点Q的坐标，求出PQ的长，即可求出S与x的函数关系式，然后利用二次函数求最值即可．

【详解】

解：（1）∵抛物线y=ax2+bx+c经过点A（﹣1，0），C（0，3），抛物线的顶点在直线上

∴

解得：

∴抛物线的解析式为；

（2）∵点A（﹣1，0），抛物线的对称轴为直线x=1

∴点B的坐标为（3,0）

设点P（x，），过点P作PQ⊥x轴，交BC于点Q

设直线BC的解析式为y=kx＋d

将点B、C的坐标代入，得

解得

∴直线BC的解析式为y=-x＋3

∴点Q的坐标为（x，-x＋3）

∴PQ=－（-x＋3）=

∴S=PQ（xB－xC）=（）×3=（）2＋

∵＜0

∴当x=时，S最大为

此时点P的坐标为（，）

【点睛】

此题考查的是二次函数的综合大题，掌握利用待定系数法求二次函数解析式、一次函数解析式和利用“铅垂高，水平宽”求面积最值是解题关键．

7．（2020·民勤县第六中学三模）如图，抛物线y=﹣x2+bx+c经过点A，B，C，已知点A（﹣1，0），点C（0，3）．

（1）求抛物线的表达式；

（2）P为线段BC上一点，过点P作y轴的平行线，交抛物线于点D，当△BDC的面积最大时，求点P的坐标；

【答案】（1）y=﹣x2+2x+3；（2）P（，）．

【解析】

【分析】

（1）根据抛物线y＝−x2＋bx＋c经过点A（−1，0），点C（0，3），可以用待定系数法求得抛物线的表达式；

（2）根据函数的解析式可以求得点B的坐标，从而可以求得直线BC的解析式，设出点P、D的坐标从而可以表示出△BDC的面积，从而可以得到点P的坐标；

【详解】

（1）∵点A（−1，0），点C（0，3）在抛物线y＝−＋bx＋c上，

∴ 

解得b＝2，c＝3．

即抛物线的表达式是；

（2）令 ，解得＝−1， ＝3，

∵点A（−1，0），

∴点B的坐标为（3，0）．

设过点B、C的直线的解析式为：y＝kx＋b

，

解得k＝−1，b＝3．

∴过点B、C的直线的解析式为：y＝−x＋3．

设点P的坐标为（a，−a＋3），则点D的坐标为（a， ），

∴PD＝（）−（−a＋3）＝．

∴S△BDC＝S△PDC＋S△PDB

＝PD•a＋PD•(3−a)

＝ ( )•a＋ ()•(3−a)

＝− ．

∴当a＝时，△BDC的面积最大，

∴点P的坐标为（，）．

【点睛】

本题是考查二次函数综合题，解题的关键是根据题意找出其中相关联的量，利用分类讨论的数学思想解答各个问题．

8．（2020·河南卧龙·期末）如图，抛物线y＝ax2+bx+3（a≠0）的对称轴为直线x＝﹣1，抛物线交x轴于A、C两点，与直线y＝x﹣1交于A、B两点，直线AB与抛物线的对称轴交于点E．

（1）求抛物线的解析式．

（2）点P在直线AB上方的抛物线上运动，若△ABP的面积最大，求此时点P的坐标．

【答案】(1)y＝﹣x2﹣2x+3；(2)点P(，)；

【解析】

【分析】

(1)令y＝0，求出点A的坐标，根据抛物线的对称轴是x＝﹣1，求出点C的坐标，再根据待定系数法求出抛物线的解析式即可；

(2)设点P(m，﹣m2﹣2m+3)，利用抛物线与直线相交，求出点B的坐标，过点P作PF∥y轴交直线AB于点F，利用S△ABP＝S△PBF+S△PFA，用含m的式子表示出△ABP的面积，利用二次函数的最大值，即可求得点P的坐标；

【详解】

解：(1)令y＝0，可得：x﹣1＝0，解得：x＝1，

∴点A(1，0)，

∵抛物线y＝ax2+bx+3(a≠0)的对称轴为直线x＝﹣1，

∴﹣1×2﹣1＝﹣3，即点C(﹣3，0)，

∴ ，解得：

∴抛物线的解析式为：y＝﹣x2﹣2x+3；

(2)∵点P在直线AB上方的抛物线上运动，

∴设点P(m，﹣m2﹣2m+3)，

∵抛物线与直线y＝x﹣1交于A、B两点，

∴ ，解得：，

∴点B(﹣4，﹣5)，

如图，过点P作PF∥y轴交直线AB于点F，

则点F(m，m﹣1)，

∴PF＝﹣m2﹣2m+3﹣m+1＝﹣m2﹣3m+4，

∴S△ABP＝S△PBF+S△PFA

＝(﹣m2﹣3m+4)(m+4)+(﹣m2﹣3m+4)(1﹣m)

＝-（m+ ）2+   ，

∴当m＝时，P最大，

∴点P(，).

【点睛】

本题考查二次函数的综合应用，解决第(2)小题中三角形面积的问题时，找到一条平行或垂直于坐标轴的边是关键．

9．（2020·广东三模）如图，抛物线与轴相交于两点（点位于点的左侧），与轴相交于点，是抛物线的顶点，直线是抛物线的对称轴，且点的坐标为．

（1）求抛物线的解析式．

（2）已知为线段上一个动点，过点作轴于点．若的面积为．

①求与之间的函数关系式，并写出自变量的取值范围；

②当取得最值时，求点的坐标．

【答案】（1）；（2）①；②当时，取得最大值，此时；

【解析】

【分析】

（1）点C坐标代入解析式可求c的值，由对称轴可求b的值，即可求解；
（2）①先求出点M，点A，点B的坐标，利用待定系数法可求BM解析式，由三角形的面积公式可求解；
②利用二次函数的性质可求解；
【详解】

（1）抛物线的对称轴为直线．

又抛物线与轴的交点为，

抛物线的解析式为．

（2）①顶点．

设直线的解析式为．

将代入，

得解得

直线的解析式为．

轴且，

的面积．

点在线段上，且，

，

故与之间的函数关系式为．

②，

当时，取得最大值；

当时，没有最小值．

综上，当时，取得最大值，此时

【点睛】

本题是二次函数综合题，考查了二次函数的性质，待定系数法求解析式，利用分类讨论思想解决问题是本题的关键．

10．（2020·山东德州·二模）如图，抛物线与x轴交于点，点，与y轴交于点C，且过点．点P、Q是抛物线上的动点．

(1)求抛物线的解析式；

(2)当点P在直线OD下方时，求面积的最大值．

【答案】(1)抛物线的表达式为：；(2)有最大值，当时，其最大值为；

【解析】

【分析】

（1）函数的表达式为：y=a（x+1）（x-3），将点D坐标代入上式，即可求解；

（2）设点，求出，根据，利用二次函数的性质即可求解；

【详解】

解：(1)函数的表达式为：，将点D坐标代入上式并解得：，

故抛物线的表达式为：…①；

(2)设直线PD与y轴交于点G，设点，

将点P、D的坐标代入一次函数表达式：并解得，直线PD的表达式为：，则，

，

∵，故有最大值，当时，其最大值为；

【点睛】

本题考查的是二次函数综合运用，涉及到解直角三角形、面积的计算等．

11．（2020·海口市第九中学其他）如图，直线y＝﹣x+3与x轴、y轴分别交于B、C两点，经过B、C两点的抛物线y＝x2+bx+c与x轴的另一个交点为A，顶点为P．

（1）求该抛物线的解析式；

（2）当0＜x＜3时，在抛物线上求一点E，使△CBE的面积有最大值；

【答案】（1）y＝x2﹣4x+3；（2）E（，﹣）；

【解析】

【分析】

（1）用直线表达式求出点B、C的坐标，将点B、C的坐标代入y＝x2+bx+c，即可求解；

（2）S△CBE＝HE×OB＝×3×（﹣x+3﹣x2+4x﹣3）＝（﹣x2+3x），即可求解；

【详解】

解：（1）y＝﹣x+3，令y＝0，则x＝3，令x＝0，则y＝3，

故点B、C的坐标为（3，0）、（0，3），

将点B、C的坐标代入y＝x2+bx+c并解得：b＝﹣4，

故抛物线的表达式为：y＝x2﹣4x+3，

令y＝0，则x＝1或3，故点A（1，0），点P（2，﹣1）；

（2）过点E作EH∥y轴交BC于点H，

设点E（x，x2﹣4x+3），则点H（x，﹣x+3）

S△CBE＝HE×OB＝×3×（﹣x+3﹣x2+4x﹣3）＝（﹣x2+3x），

∵﹣＜0，当x＝时，S△CBE有最大值，

点E（，﹣）；

【点睛】

主要考查了二次函数的解析式的求法与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．