北师大版八年级下册第三章 图形的平移与旋转综合与测试教学课件ppt

这是一份北师大版八年级下册第三章 图形的平移与旋转综合与测试教学课件ppt，文件包含北师大版数学八年级下册第三章图形的平移与旋转-章末复习教学课件ppt、北师大版数学八年级下册第三章图形的平移与旋转-章末复习教案doc等2份课件配套教学资源，其中PPT共23页， 欢迎下载使用。
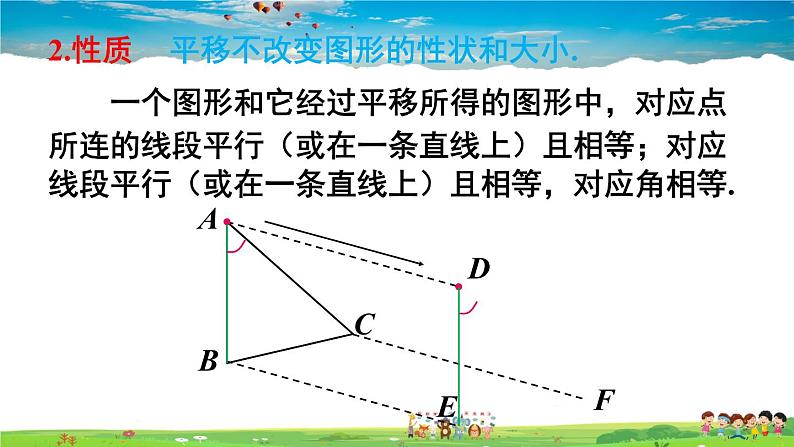
一个图形和它经过平移所得的图形中，对应点所连的线段平行（或在一条直线上）且相等；对应线段平行（或在一条直线上）且相等，对应角相等.
平移不改变图形的性状和大小.
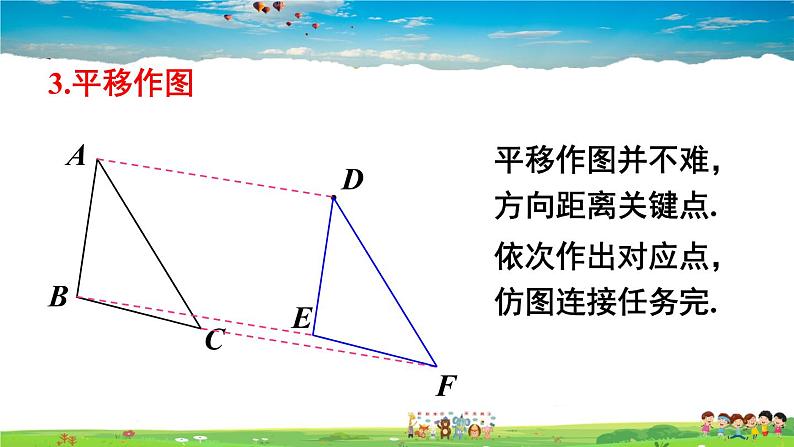
平移作图并不难，方向距离关键点.依次作出对应点，仿图连接任务完.
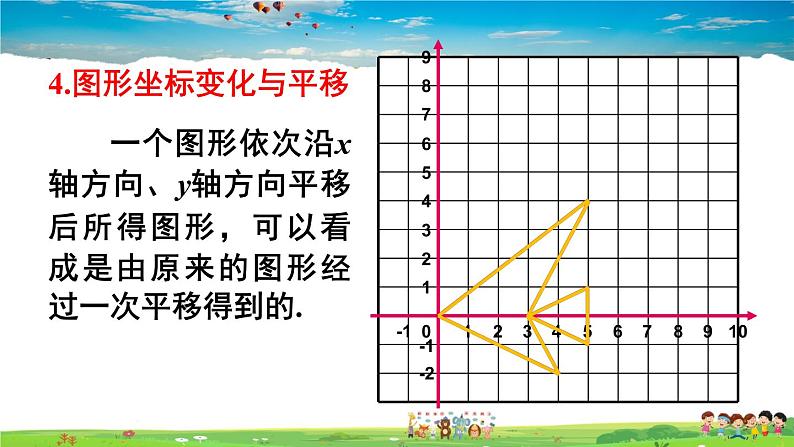
4.图形坐标变化与平移
一个图形依次沿x轴方向、y轴方向平移后所得图形，可以看成是由原来的图形经过一次平移得到的.
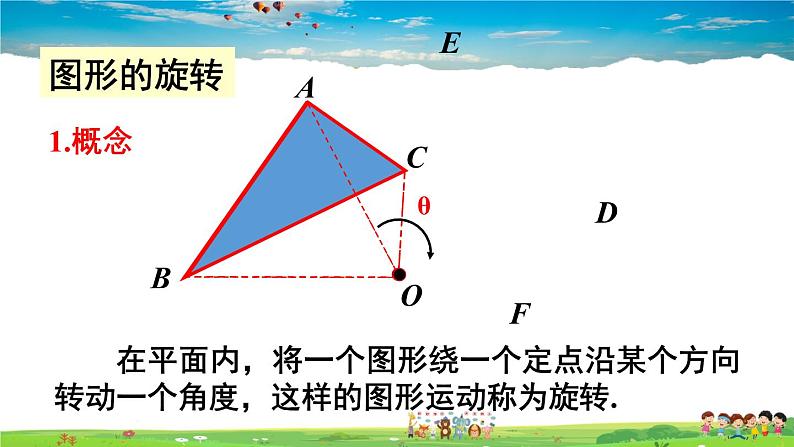
在平面内，将一个图形绕一个定点沿某个方向转动一个角度，这样的图形运动称为旋转.
a.经过旋转，图形上的每一点都绕旋转中心沿相同方向转动了相同的角度.b.旋转图形的任意一对对应点与旋转中心的连线所成的角都是旋转角.c.旋转图形的任意一对对应点到旋转中心的距离相等.d.旋转后的图形与原图形全等.（旋转不改变图形的形状和大小）
3.旋转作图的一般步骤
a.定：确定旋转中心、旋转方向及旋转角.b.找：找出构成图形的关键点.c.旋：沿一定的方向，按一定的角度，通过截取线段的方法，旋转各个关键点.d.连：顺次连接各个关键的对应点，并标上相应字母.e.写：根据作图要求写出所作的图形.
如果把一个图形绕着某一点旋转180°，它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称.
（2）关于中心对称的两个图形，对称点所连线段都经过对称中心，而且被对称中心平分．
（1）关于中心对称的两个图形是全等形；
概念 把一个图形绕某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形，这个点叫做它的对称中心.
中心对称与中心对称图形是两个既有联系又有区别的概念.
区别: 中心对称指两个全等图形的相互位置关系，中心对称图形指一个图形本身成中心对称.
联系: 如果将成中心对称的两个图形看成一个整体,则它们是中心对称图形. 如果将中心对称图形对称的部分看成两个图形,则它们成中心对称.
(1) 确定“基本图案”；
(2) 分析轴对称、平移、旋转等变换手法及组合的合理运用.
运用平移、旋转或轴对称设计简单的图案
1.下列图形中可由其中的部分图形经过平移得到的是（ ）
2. 如图，将△ABC向右平移5个单位长度，再向上平移3个单位长度得到△A1B1C1，请回答下列问题:(1)平移后的三个顶点坐标分别为:A1（___ , ___）B1（___ , ___）C1（___ , ___）
(2)画出平移后的△A1B1C1;
3.如图所示，在Rt△ABC中，BC是斜边，P是三角形内一点,将△ABP绕点A逆时针旋转后，能与△ACP′重合．如果AP＝3，则PP′的长为_______．
4.如图，是用围棋子摆出的图案(棋子的位置用有序数对表示，如A点在(5,1)．如果再摆一黑一白两枚棋子，使9枚棋子组成的图案既是轴对称图形又是中心对称图形，则下列摆放正确的是（ ）A．黑(3,3),白(3,1) B．黑(3,1),白(3,3)C．黑(1,5),白(5,5) D．黑(3,2),白(3,3)
5.据悉，浙江理工大学艺术与设计学院王晓林老师的地铁标志设计作品成功中标．它以地铁隧道为主体造型元素,充分体现了杭州地铁“安全、快捷、顺畅、方便、舒适”的特点．该图主要运用的数学变换原理是（ ）A．平移、对称变换 B．对称、旋转变换C．相似、平移变换 D．旋转、相似变换
谈谈你在这节课中，有什么收获？