初中数学北师大版八年级下册1 等腰三角形教学ppt课件

这是一份初中数学北师大版八年级下册1 等腰三角形教学ppt课件，共17页。PPT课件主要包含了学习目标，问题导入，讲授新课等内容，欢迎下载使用。

1. 探索一个三角形成为等边三角形的条件并证明正确性.2.探究有30°角的直角三角形的性质及推理过程.3.运用所学知识进行相关的证明和计算.
　　问题　已知△ABC 中，∠A =60°,（         ）. 请你在括号内补充一个条件，使△ABC 能成为等边三角形.
∠B =60°（或∠C =60°）AB =BC，AC =BC，AB =BC =AC.
　　思考2　这个特殊的直角三角形相比一般的直角三角形有什么不同之处，它有什么特殊性质？
　　思考1　等边三角形是轴对称图形，若沿着其中一 条对称轴折叠，能产生什么特殊图形？
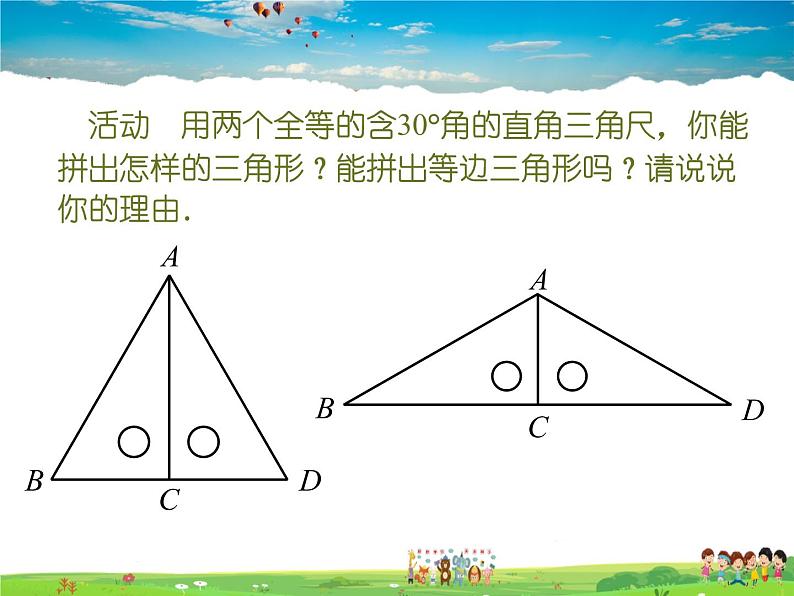
　　活动　用两个全等的含30°角的直角三角尺，你能拼出怎样的三角形？能拼出等边三角形吗？请说说你的理由．
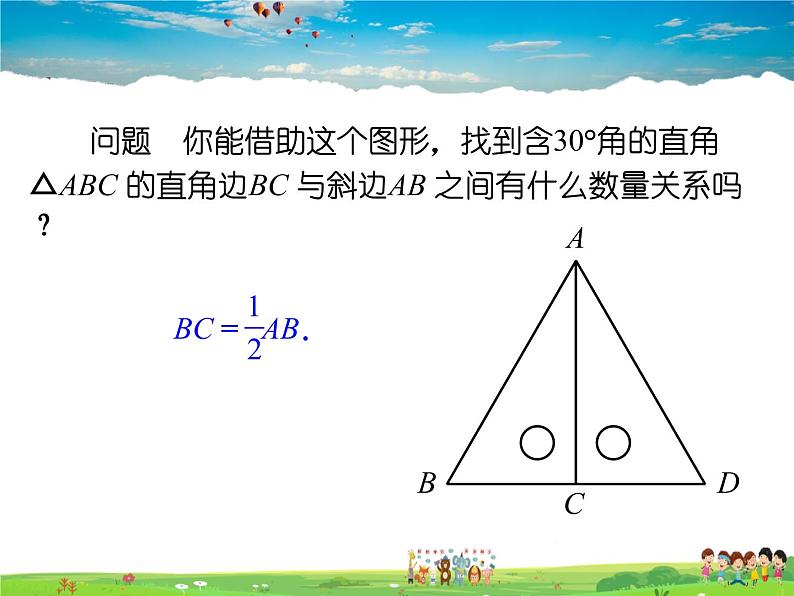
　　问题　你能借助这个图形，找到含30°角的直角 △ABC 的直角边BC 与斜边AB 之间有什么数量关系吗？
　　思考　这个命题是真命题吗？请进行证明．
　　问题　请说一说你猜想的命题中，条件和结论分别是什么？并结合图形，用符号语言表述出来.
　　猜想　在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.
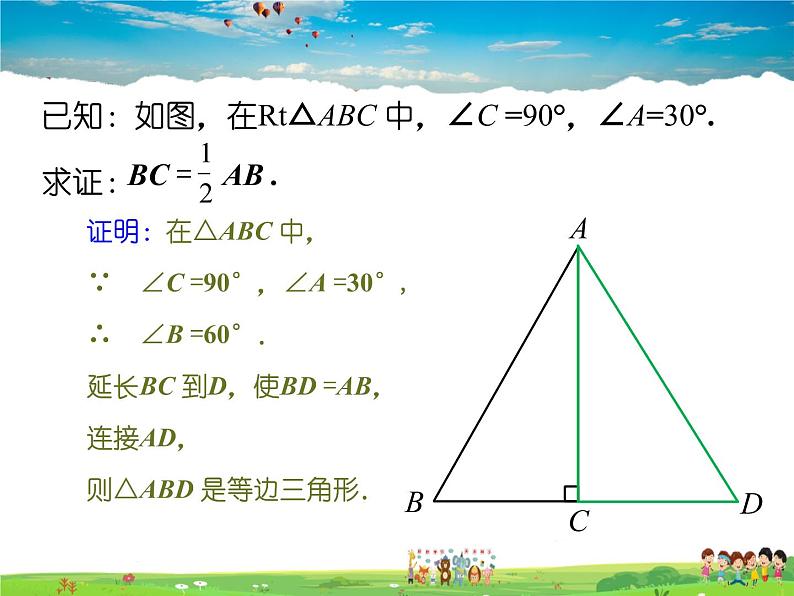
证明：在△ABC 中，∵　∠C =90°，∠A =30°, ∴　∠B =60°．延长BC 到D，使BD =AB，连接AD，则△ABD 是等边三角形．
已知：如图，在Rt△ABC 中，∠C =90°，∠A=30°. 求证：
　　追问：你还能用其他方法证明吗？
证明：由等边三角形的性质可知，AC 也是BD 边上的中线，
另证：作∠BCE =60°，交AB于E，连接CE， 则∠ACE =90°-60°=30°．在△ABC 中，∵　∠ACB=90°，∠A =30°，∴　∠B =60°．在△BCE 中，∵　∠BCE=60°，∠B =60°，∴　△BCE 是等边三角形．∴　BC =BE =CE．
符号语言：∵　在Rt△ABC 中，　　∠C =90°，∠A =30°，　　
　　在直角三角形中，如果一个锐角等于30°，那么 它所对的直角边等于斜边的一半.
　　例1　如图，在△ABC 中，∠ACB =90°，CD 是 高，∠A =30°，AB =4．则BD = .
例2.已知：如图，在△ABC中,高线BD和CE相交于H，∠BHC=120°,HD=1,HE=3,求BD和CE的长.
CH=2CE=5BH=6BD=7
例3.将不全等的两个等边三角形△ABC和等边三角形△DEF任意摆放,请你画出不少于5种的摆放示意图,使得AE=CF,同时满足在重合的一条直线上有且只有三个顶点(重合的顶点算一个),并说明理由.
例4 矩形ABCD中,AB=6,BC=8,先把它对折,折痕为EF展开后再折成如图所示,使点A落在EF上的点A'处,求第二次折痕BG的长.
例5.已知正方形ABCD中,M是AB的中点,E是AB延长线上的一点,MN⊥DM,且交∠CBE的平分线于N. (1)求证:MD=MN；
(2)若将上述条件中的“M是AB的中点”改为“M是AB上的任意一点”，其它条件不变，则结论“MD=MN”还成立吗？如果成立请证明；若不成立请说明理由