






(广西版)中考数学总复习课件19《角、相交线与平行线》(含答案)
展开角 角平分线 相交线 垂线 平行线
1.角的相关概念:由具有 的两条射线组成的图形叫做角. 当角的两边在一条直线上时,组成的角叫做平角.平角的一半叫做直角;小于直角的角叫做锐角;大于直角且小于平角的角叫做钝角.如果两个角的和是90°,那么这两个角叫做互为 . 如果两个角的和是180°,那么这两个角叫做互为 . 2.角的平分线及性质:端点为角的顶点的一条射线把这个角分成两个相等的角,这条射线叫做这个角的 . 角的平分线有下面的性质定理:(1)角平分线上的点到这个角的两边的距离 . (2)角的内部到这个角的两边的距离相等的点在这个角的 上.
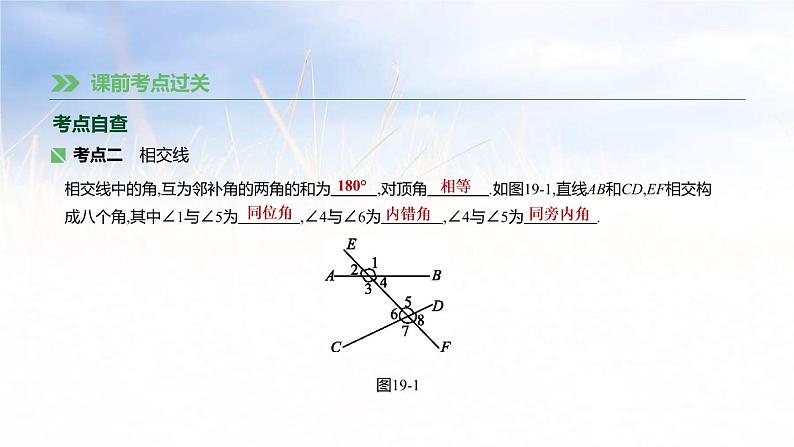
相交线中的角,互为邻补角的两角的和为 ,对顶角 .如图19-1,直线AB和CD,EF相交构成八个角,其中∠1与∠5为 ,∠4与∠6为 ,∠4与∠5为 .
1.垂线:两条直线相交所成的四个角中,当有一个角是直角时,就说这两条直线互相 .其中一条直线叫做另一条直线的 ,它们的交点叫做 . 2.垂线的性质:性质1:同一平面内,过一点有且只有一条直线与已知直线垂直.性质2:垂线段最短.
1.平行线的概念:在同一个平面内,不相交的两条直线叫做平行线.同一个平面内,两条直线的位置关系只有两种: . 2.平行公理及其推论:平行公理:经过直线外一点,有且只有一条直线与这条直线 . 推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
3.平行线的判定:(1)同位角 ,两直线平行; (2)内错角 ,两直线平行; (3)同旁内角 ,两直线平行. (4)其他平行线的判定方法:①平行线的定义;②平行于同一直线的两直线平行;③同一平面内垂直于同一直线的两直线平行.4.平行线的性质:(1)两直线平行,同位角 ; (2)两直线平行,内错角 ; (3)两直线平行,同旁内角 .
1.如图19-2所示,点P到直线l的距离是( )A.线段PA的长度 B.线段PB的长度C.线段PC的长度 D.线段PD的长度
[解析] 点P到直线l的距离就是过点P作直线l的垂线段的长度.
2.如图19-3,直线a,b被直线c所截,若a∥b,∠1=110°,则∠2等于( )A.70° B.75° C.80° D.85°
3.如图19-4,直线AB与CD相交于点O,EO⊥CD,垂足为O.若∠EOB=130°,则∠AOC的大小为( ) A.40°B.50° C.90° D.130°
[解析] 由EO⊥CD,得出∠EOD=90°,由∠BOD=∠EOB-∠EOD,可求出∠BOD的度数,利用对顶角相等即可求出∠AOC的大小.∵EO⊥CD,∴∠EOD=90°.∵∠EOB=130°,∴∠BOD=∠EOB-∠EOD=130°-90°=40°,∴∠AOC=40°.
4.如图19-5,下面推理中,正确的是( )A.∵∠A+∠D=180°,∴AD∥BCB.∵∠C+∠D=180°,∴AB∥CDC.∵∠A+∠D=180°,∴AB∥CDD.∵∠A+∠C=180°,∴AB∥CD
5.[2018·柳北区4月模拟] 如图19-6,O为直线AB上一点,OE平分∠BOC,OD⊥OE于点O,若∠BOC=80°,则∠AOD的度数是( )A.70°B.50°C.40°D.35°
6.如图19-7,直线a∥b,∠BAC的顶点A在直线a上,且∠BAC=100°.若∠1=34°,则∠2= °.
7.若一个角的度数是它的余角的2倍,则这个角的补角的度数是 .
[解析] 因为a∥b,所以∠1+∠BAC+∠2=180°.所以∠2=180°-∠BAC-∠1=180°-100°-34°=46°.
[解析] 设这个角为x°,则它的余角为(90-x)°.由题意可得x=2(90-x).解得x=60.∴它的补角为180°-60°=120°.
【失分点】 错误认为同位角、内错角、同旁内角与两直线是否平行有关;有关三角板、量角器类角度计算题,不能抽象为数学问题
8.[2018·金华、丽水] 如图19-8,∠B的同位角可以是( )A.∠1 B.∠2C.∠3 D.∠4
9.[2018·绵阳] 如图19-9,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=44°,那么∠1的度数是( )A.14° B.15°C.16° D.17°
例1 [2018·厦门质检] 在同一条直线上依次有A,B,C,D四个点,若CD-BC=AB,则下列结论正确的是( )A.B是线段AC的中点B.B是线段AD的中点C.C是线段BD的中点D.C是线段AD的中点
拓展1 [2016·柳州] 如图19-10,在直线l上有A,B,C三点,则图中线段共有( )A.1条 B.2条C.3条 D.4条
拓展2 如图19-11,AM为∠BAC的平分线,下列等式错误的是( )
例2 如图19-12,直线AB,CD交于点O,∠1=∠2.(1)指出∠3的对顶角;(2)指出∠5的补角;(3)若∠1与∠4的度数之比为1∶4,求∠3的度数.
解:(1)∠3的对顶角是∠2.
解: (2)∠5的补角是∠1,∠2,∠3.
拓展1 [2015·柳州] 如图19-13,图中∠α的度数等于( )A.135°B.125°C.115°D.105°
拓展2 如图19-14,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠AOC=50°,则∠DOE等于( )A.30° B.40° C.50° D.60°
[解析] ∵∠AOC=50°,∴∠BOD=50°.∴∠DOE=90°-50°=40°.
例3 如图19-15,已知∠ABC=180°-∠A,BD⊥CD于点D,EF⊥CD于点F.(1)求证:AD∥BC;(2)若∠1=36°,求∠2的度数.
解:(1)证明:∵∠ABC=180°-∠A,∴∠ABC+∠A=180°.∴AD∥BC.
解: (2)∵AD∥BC,∠1=36°, ∴∠DBC=∠1=36°.∵BD⊥CD,EF⊥CD, ∴BD∥EF.∴∠2=∠DBC=36°.
拓展1 [2018·城中区第十二中模拟] 如图19-16,直线AB∥CD,∠A=40°,∠D=45°,则∠1的度数是( )A.80° B.85°C.90° D.95°
[解析] ∵AB∥CD,∴∠A=∠C=40°,∵∠1=∠D+∠C,∠D=45°,∴∠1=∠D+∠C=45°+40°=85°,故选B.
拓展2 [2018·柳州] 如图19-17,a∥b,若∠1=46°,则∠2= °.
拓展3 [2018·永州] 一副透明的三角板,如图19-18所示叠放,直角三角板的斜边AB,CE相交于点D,则∠BDC= .
教材母题——人教版七下P37练习T13(1)完成下面的证明.如图19-19,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA,求证∠FDE=∠A.证明:∵DE∥BA,∴∠FDE= ( ). ∵DF∥CA,∴∠A= ( ). ∴∠FDE=∠A.
两直线平行,内错角相等
两直线平行,同位角相等
(广西版)中考数学总复习课件23《直角三角形与勾股定理》(含答案): 这是一份(广西版)中考数学总复习课件23《直角三角形与勾股定理》(含答案),共30页。PPT课件主要包含了考点自查,斜边的一半,斜边上的中线,a2+b2c2,对点自评,图23-1,图23-3,答案D,答案A,答案4cm等内容,欢迎下载使用。
(广西版)中考数学总复习课件3《整式》(含答案): 这是一份(广西版)中考数学总复习课件3《整式》(含答案),共20页。PPT课件主要包含了考点自查,a2-b2,a2±2ab+b2,对点自评,②③④,-a6,图3-1等内容,欢迎下载使用。
(广西版)中考数学总复习课件22《等腰三角形》(含答案): 这是一份(广西版)中考数学总复习课件22《等腰三角形》(含答案),共26页。PPT课件主要包含了考点自查,等边对等角,三线合一,等边三角形,两个端点,距离相等,对点自评,图22-1,图22-2,答案A等内容,欢迎下载使用。












