北师大版八年级上册1 探索勾股定理评课课件ppt

这是一份北师大版八年级上册1 探索勾股定理评课课件ppt，共12页。PPT课件主要包含了情景导入，思考探究获取新知，观察与发现，你发现了吗，数学小知识，随堂练习等内容，欢迎下载使用。

我们知道，任意三角形的三条边必须满足定理：三角形的两边之和大于第三边。
对于一些特殊的三角形，是否还存在其他特殊的关系？
1.在纸上画若干个直角三角形，分别测量它们的三条边，看看三边长的平方之间有怎么样的关系？
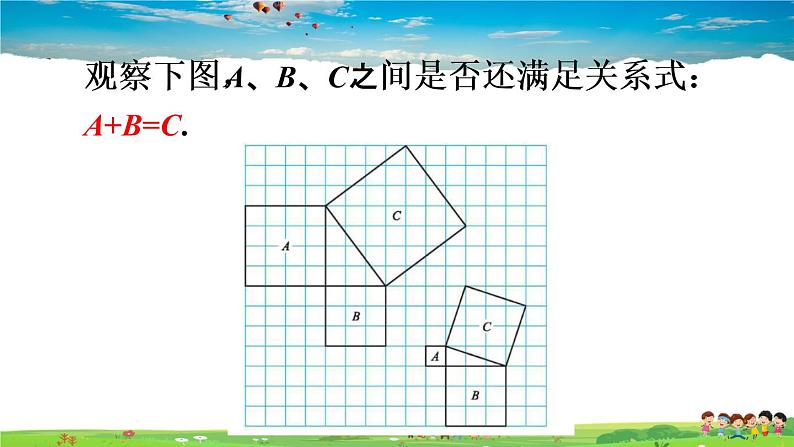
观察图形，正方形A中有 个小方格，即A的面积为 个面积单位。正方形B中有 个小方格，即B的面积为 个面积单位。正方形C中有 个小方格，即C的面积为 个面积单位。
你发现A、B、C的面积之间有什么关系？
归纳得出结论：A+B=C
观察下图，A、B、C之间是否还满足关系式：A+B=C.
如果直角三角形两直角边分别是1.6个单位长度和2.4个单位长度，前面所猜想的数量关系式还成立吗？
直角三角形的两直角边的平方和等于斜边的平方，这就是著名的“勾股定理”。 如果直角三角形的两条直角边为a、b，斜边为c，那么有a2+b2=c2.
我国古代称直角三角形的较短的直角边为勾，较长的直角边为股，斜边为弦，这便是勾股定理的由来。
1.求下图中字母所代表的正方形的面积。
解:A 所代表的正方形的面积是625；B 所代表的正方形的面积是144．
2.在直角三角形ABC中，∠C=90°，若a=5，b=12，则c= 。 3.在直角三角形ABC中，∠C=90°，若a=5，c=10，则b= 。 4.在直角三角形ABC中，它的两直角边长的比是 3:4，斜边长是20，则两直角边长分别是 、 。