考点04 导数与函数的极值、最值-高考数学（理）一轮复习小题多维练（全国通用）（解析版）

这是一份考点04 导数与函数的极值、最值-高考数学（理）一轮复习小题多维练（全国通用）（解析版），共14页。试卷主要包含了单选题等内容，欢迎下载使用。
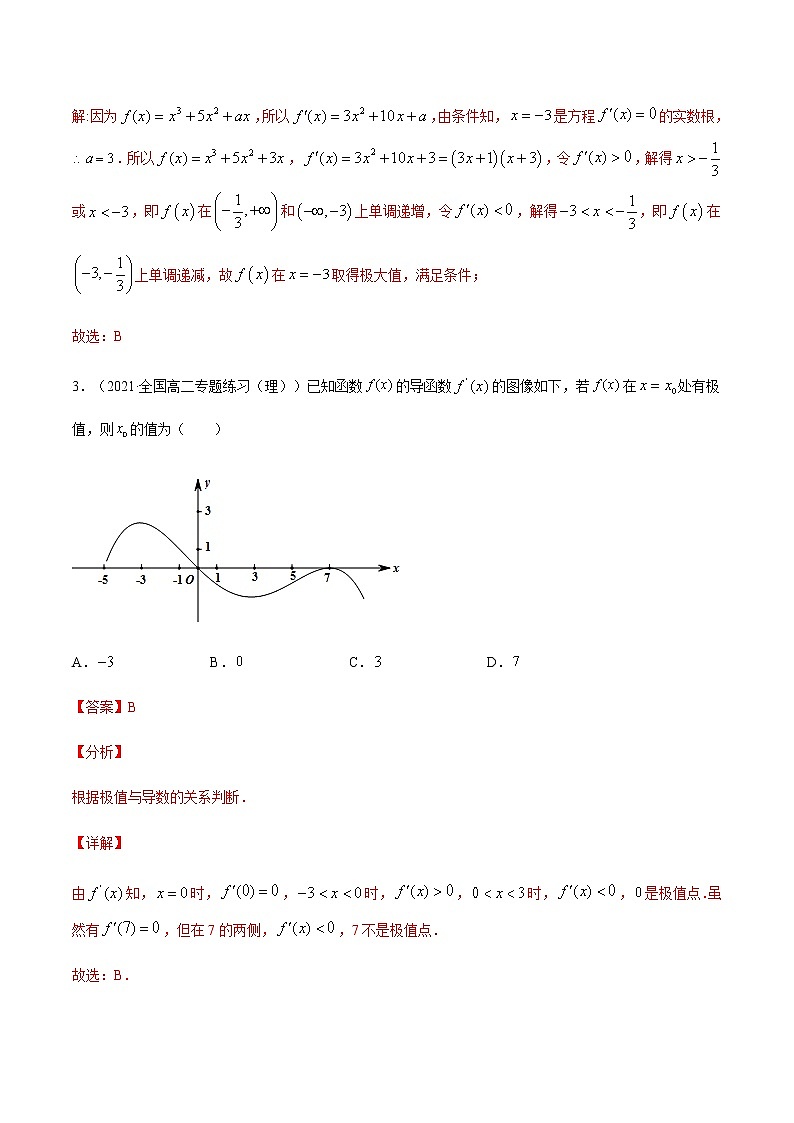
考点04 导数与函数的极值、最值 一、单选题1．（2014·全国陕西省·高三一模）已知e为自然对数的底数，设函数f（x）=xex，则A．1是f（x）的极小值点 B．﹣1是f（x）的极小值点C．1是f（x）的极大值点 D．﹣1是f（x）的极大值点【答案】B【详解】试题分析：，当时，，当时，，当时，，所以当时，函数取得极小值，是函数的极小值点，故选B.考点：导数与极值2．（2021·河南（理））已知函数在处取得极值，则（    ）A．4 B．3 C．2 D．【答案】B【分析】依题意，即可求出参数的值；【详解】解:因为，所以，由条件知，是方程的实数根，．所以，，令，解得或，即在和上单调递增，令，解得，即在上单调递减，故在取得极大值，满足条件；故选：B3．（2021·全国高二专题练习（理））已知函数的导函数的图像如下，若在处有极值，则的值为（    ）A． B． C． D．【答案】B【分析】根据极值与导数的关系判断．【详解】由知，时，，时，，时，，是极值点．虽然有，但在7的两侧，，7不是极值点．故选：B．4．（2020·河南南阳市·高二期中（理））已知是函数就函数的极小值点，那么函数的极大值为（    ）A．-2 B．6 C．17 D．18【答案】D【分析】求出导数，由题意得，，解出，再由单调性，判断极大值点，求出即可．【详解】函数的导数， 由题意得，，即，． ，，令，得或；，得， 所以当时取极大值，即． 故选：D．【点睛】本题考查导数的应用：求极值，同时考查运算能力，属于基础题．5．（2019·四川省绵阳南山中学高二期中（理））已知是上的连续可导函数，则“”是“是函数的一个极值点”的条件.A．充分不必要 B．必要不充分C．充要 D．既不充分又不必要【答案】B【分析】由极值点的定义可以判定条件不能推结论，结论可以推条件，再由充分必要性的判定，即可判定答案.【详解】因为是上的连续可导函数条件中，只能说明是一个驻点，该点处两边的单调性不一定相异，所以不一定是极值点，故不可推出结论结论中是函数的一个极值点，则该点处的导数必然，故可以推出条件所以是必要不充分条件故选：B【点睛】本题考查函数中极值点的定义，还考查了充分必要条件的判定，属于基础题.6．（2021·江西赣州市·高二期末（理））若函数在处有极大值，则常数c为（    ）A．1 B．3 C．1或3 D．-1或-3【答案】B【分析】求出函数的导数，再令导数等于0，求出 值，再检验函数的导数是否满足在处左侧为正数，右侧为负数，把不满足条件的值舍去．【详解】函数，，由题意知，在处的导数值为，，或，又函数在处有极大值，故导数值在处左侧为正数，右侧为负数．当时，，满足导数值在处左侧为正数，右侧为负数．当时，，导数值在处左侧为负数，右侧为正数．故．故选：B．7．（2020·全国高二课时练习）设三次函数f(x)的导函数为f′(x)，函数y＝xf′(x)的图象的一部分如图所示，则（    ）A．f(x)极大值为f()，极小值为f(－) B．f(x)极大值为f(－)，极小值为f()C．f(x)极大值为f(－3)，极小值为f（3） D．f(x)极大值为f（3），极小值为f(－3)【答案】D【分析】利用导数与函数单调性之间的关系以及极值的定义即可得出结果.【详解】当x<－3时，y＝xf′(x)>0，即f′(x)<0；当－3<x<3时，f′(x)≥0；当x>3时，f′(x)<0．∴f(x)的极大值是f（3），f(x)的极小值是f(－3)． 故选：D8．（2021·河北沧州市·高三三模）已知函数，则（    ）A．的单调递减区间为 B．的极小值点为1C．的极大值为 D．的最小值为【答案】C【分析】先对函数求导，令，再利用导数判断其单调性，而，从而可求出的单调区间和极值【详解】.令，则，所以在上单调递减.因为，所以当时，；当时，.所以的单调递增区间为，单调递减区间为，故的极大值点为1，的极大值为故选：C9．（2021·河南开封市·高三三模（理））设函数，若的极小值为，则（    ）A． B． C． D．2【答案】B【分析】由函数的导数求极值点，将极值点代入可得方程，进而求得值.【详解】由已知得：，令，有，且上递减，上递增，∴的极小值为，即，得.故选：B.10．（2021·全国高三其他模拟（理））函数的最小值为（    ）A． B． C． D．0【答案】B【分析】首先利用导数求出函数的单调区间，再根据单调区间即可得到最小值.【详解】，令，解得.所以在上单调递减，在上单调递增，故的最小值为．故选：B11．（2021·河南郑州市·高二期末（理））若函数在区间上有最大值，则实数的取值范围是（    ）A． B． C． D．【答案】D【分析】求导，求得其最大值点，再根据在区间上有最大值，由最大值点的横坐标是中的元素求解.【详解】因为函数，所以，当或时，，当时，，所以当时，取得最大值，又，且在区间上有最大值，所以，解得，所以实数的取值范围是故选：D12．（2020·全国）若函数在区间上存在最小值，则实数m的取值范围是（    ）A． B． C． D．【答案】D【分析】求导，可得的单调区间和极值点，根据题意，可得，经检验符合题意，即可得答案.【详解】函数的导函数为，令，得或，故在上单调递增，在上单调递减，则为极小值点，为极大值点.由在区间上存在最小值，可得，解得，此时，因此实数m的取值范围是，故选：D.13．（2021·全国高考真题（理））设，若为函数的极大值点，则（    ）A． B． C． D．【答案】D【分析】结合对进行分类讨论，画出图象，由此确定正确选项.【详解】若，则为单调函数，无极值点，不符合题意，故.依题意，为函数的极大值点，当时，由，，画出的图象如下图所示：由图可知，，故.当时，由时，，画出的图象如下图所示：由图可知，，故.综上所述，成立.故选：D【点睛】本小题主要考查三次函数的图象与性质，利用数形结合的数学思想方法可以快速解答.14．（2019·辽宁高考真题（理））设函数满足则时，A．有极大值，无极小值 B．有极小值，无极大值C．既有极大值又有极小值 D．既无极大值也无极小值【答案】D【详解】函数满足，，令，则，由，得，令，则在上单调递减，在上单调递增，的最小值为.又在单调递增，既无极大值也无极小值，故选D.考点：1、利用导数研究函数的单调性；2、利用导数研究函数的极值及函数的求导法则.【方法点睛】本题主要考察抽象函数的单调性以及函数的求导法则，属于难题.求解这类问题一定要耐心读题、读懂题，通过对问题的条件和结论进行类比、联想、抽象、概括，准确构造出符合题意的函数是解题的关键；解这类不等式的关键点也是难点就是构造合适的函数，构造函数时往往从两方面着手：①根据导函数的“形状”变换不等式“形状”；②若是选择题，可根据选项的共性归纳构造恰当的函数.本题通过观察导函数的“形状”，联想到函数，再结合条件判断出其单调性，进而得出正确结论.15．（2020·重庆高考真题（理））设函数在R上可导，其导函数为 ，且函数的图像如题（8）图所示，则下列结论中一定成立的是A．函数有极大值 和极小值B．函数有极大值 和极小值C．函数有极大值 和极小值D．函数有极大值 和极小值【答案】D【详解】则函数增；则函数减；则函数减；则函数增；选D.【考点定位】判断函数的单调性一般利用导函数的符号，当导函数大于0则函数递增，当导函数小于0则函数递减16．（2018·全国高考真题（理））若是函数的极值点，则的极小值为．A． B． C． D．【答案】A【详解】由题可得，因为，所以，，故，令，解得或，所以在上单调递增，在上单调递减，所以的极小值为，故选A．【名师点睛】（1）可导函数y＝f(x)在点x0处取得极值的充要条件是f ′(x0)＝0，且在x0左侧与右侧f ′(x)的符号不同；（2）若f(x)在(a，b)内有极值，那么f(x)在(a，b)内绝不是单调函数，即在某区间上单调增或减的函数没有极值．