






- 12.2.1《边边边》课件+教案+练习 课件 5 次下载
- 12.2.2《边角边》课件+教案+练习 课件 1 次下载
- 12.2.3《角边角和角角边》课件+教案+练习 课件 4 次下载
- 12.2.4《斜边直角边》课件+教案+练习 课件 2 次下载
- 12.3.1《角平分线的性质》课件+教案+练习 课件 5 次下载
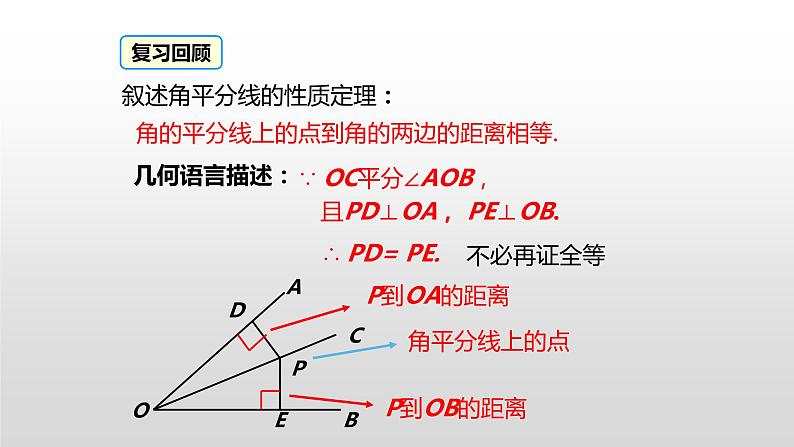
初中数学人教版八年级上册12.3 角的平分线的性质一等奖ppt课件
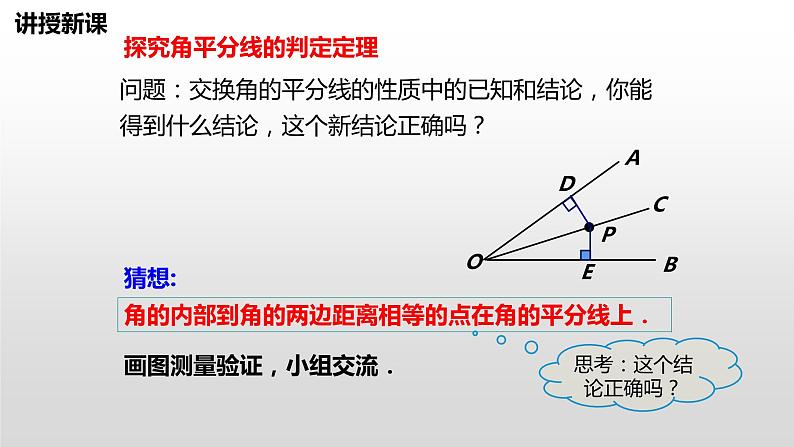
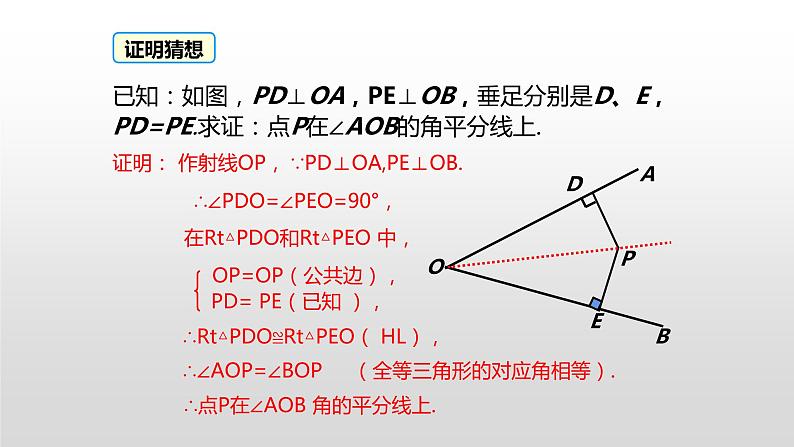
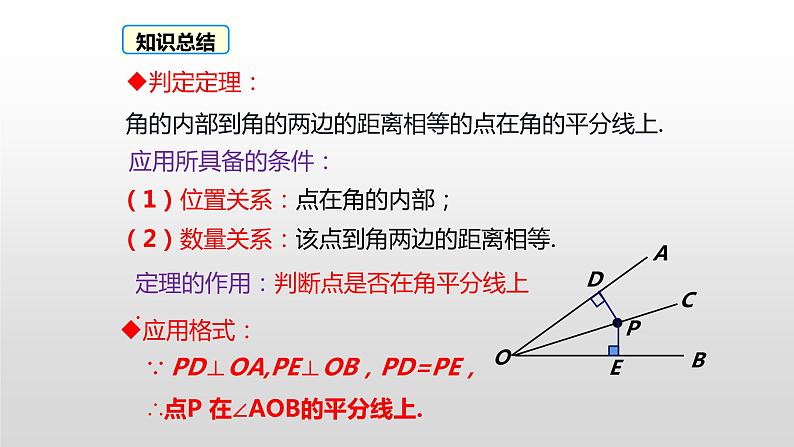
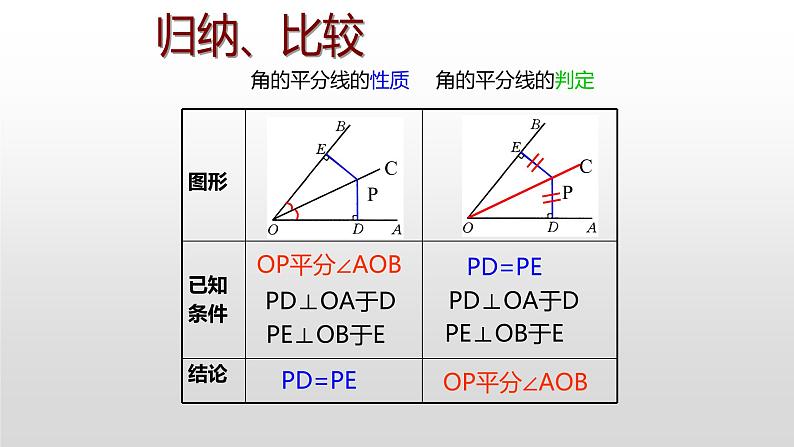
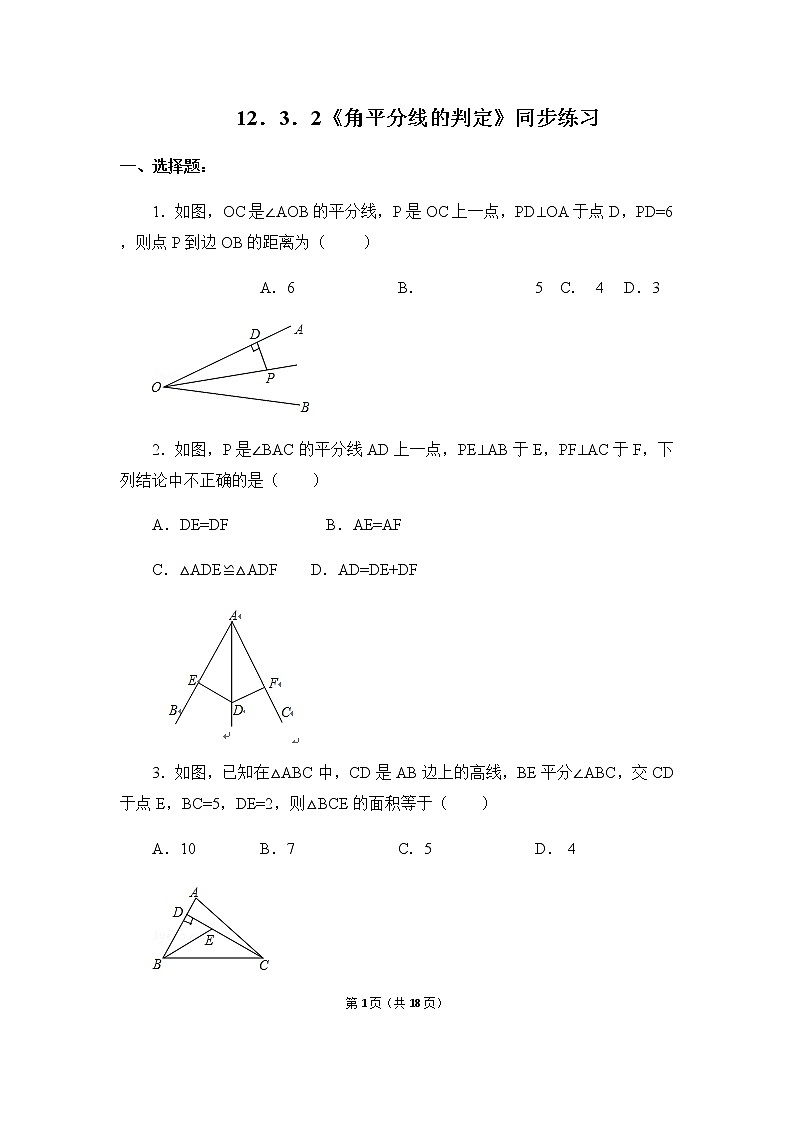
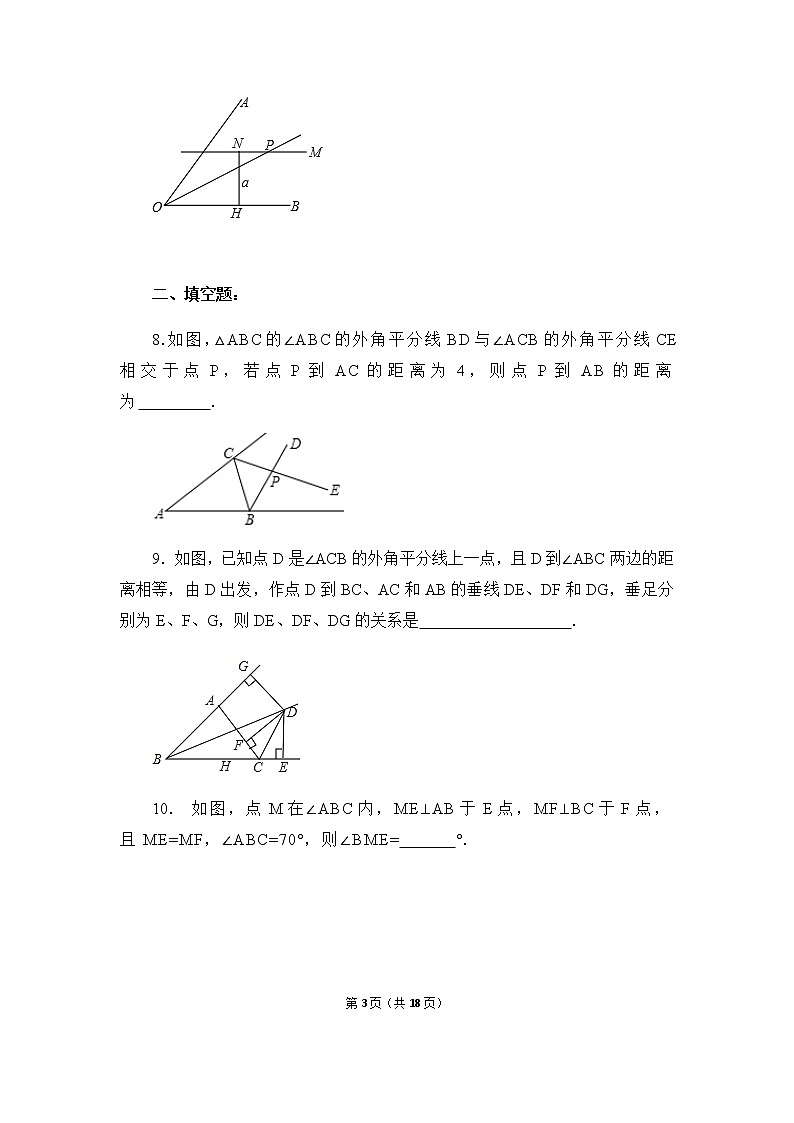
展开12.3.2《角平分线的判定》 (人教版初中数学八年级上册)复习回顾ODPP到OA的距离P到OB的距离角平分线上的点几何语言描述:∵ OC平分∠AOB, 且PD⊥OA, PE⊥OB.∴ PD= PE.ACB角的平分线上的点到角的两边的距离相等.叙述角平分线的性质定理:不必再证全等E我们知道,角平分线上的点到角的两边的距离相等.那么到角的两边的距离相等的点是否在角的平分线上呢?到角的两边的距离相等的点在角的平分线上.引入新课讲授新课角的内部到角的两边距离相等的点在角的平分线上.问题:交换角的平分线的性质中的已知和结论,你能得到什么结论,这个新结论正确吗?猜想:思考:这个结论正确吗?探究角平分线的判定定理画图测量验证,小组交流.已知:如图,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=PE.求证:点P在∠AOB的角平分线上.证明:作射线OP, ∴点P在∠AOB 角的平分线上. 在Rt△PDO和Rt△PEO 中,(全等三角形的对应角相等). OP=OP(公共边),PD= PE(已知 ),∵PD⊥OA,PE⊥OB.∴∠PDO=∠PEO=90°,∴Rt△PDO≌Rt△PEO( HL),∴∠AOP=∠BOP证明猜想所以: 角平分线可以看做到角的两边距离相等的所有点的集合.角的内部到角的两边距离相等的点在角的平分线上.明确结论判定定理:角的内部到角的两边的距离相等的点在角的平分线上.应用所具备的条件:定理的作用:判断点是否在角平分线上.应用格式:∵ PD⊥OA,PE⊥OB,PD=PE,∴点P 在∠AOB的平分线上.知识总结角的平分线的性质OP平分∠AOBPD⊥OA于DPE⊥OB于EPD=PEOP平分∠AOBPD=PEPD⊥OA于DPE⊥OB于E角的平分线的判定归纳、比较典例精析 例1:如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500米,这个集贸市场应建在何处(比例尺为1︰20000)?DCS解:作夹角的角平分线OC,截取OD=2.5cm ,D即为所求.O方法点拨:根据角平分线的判定定理,要求作的点到两边的距离相等,一般需作这两边直线形成的角的平分线,再在这条角平分线上根据要求取点.活动1 分别画出下列三角形三个内角的平分线,你发现了什么?发现:三角形的三条角平分线相交于一点探究三角形的内角平分线的性质活动2 分别过交点作三角形三边的垂线,用刻度尺量一量,每组垂线段,你发现了什么?发现:过交点作三角形三边的垂线段相等你能证明这个结论吗?已知:如图,△ABC的角平分线BM,CN相交于点P,求证:点P到三边AB,BC,CA的距离相等.证明结论证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.∵BM是△ABC的角平分线,点P在BM上,∴PD=PE.同理PE=PF.∴PD=PE=PF.即点P到三边AB,BC,CA的距离相等.D E F 想一想:点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?点P在∠A的平分线上.D E F 结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.EO变式1:如图,在直角△ABC中,∠C=90°,AP平分∠BAC,BD平分∠ABC;AP,BD交于点O,过点O作OM⊥AC,若OM=4,(1)求点O到△ABC三边的距离和.温馨提示:不存在垂线段———构造应用12解:连接OC变式2:如图,在直角△ABC中,∠C=90°,AP平分∠BAC,BD平分∠ABC;AP,BD交于点O,过点O作OM⊥AC,若OM=4.(2)若△ABC的周长为32,求△ABC的面积.1.应用角平分线性质:存在角平分线涉及距离问题2.联系角平分线性质:距离面积周长条件知识与方法例2 如图,在△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等.若∠A=40°,则∠BOC的度数为( )A.110° B.120° C.130° D.140°A解析:由已知,O到三角形三边的距离相等,所以O是内心,即三条角平分线的交点,AO,BO,CO都是角平分线,所以有∠CBO=∠ABO= ∠ABC,∠BCO=∠ACO= ∠ACB,∠ABC+∠ACB=180°-40°=140°,∠OBC+∠OCB=70°,∠BOC=180°-70°=110°. 由已知,O 到三角形三边的距离相等,得O是内心,再利用三角形内角和定理即可求出∠BOC的度数.方法总结归纳总结角的平分线的性质OP平分∠AOBPD⊥OA于DPE⊥OB于EPD=PEOP平分∠AOBPD=PEPD⊥OA于DPE⊥OB于E角的平分线的判定当堂练习1. 如图,某个居民小区C附近有三条两两相交的道路MN、OA、OB,拟在MN上建造一个大型超市,使得它到OA、OB的距离相等,请确定该超市的位置P.小区CAOBMN2. 如图所示,已知△ABC中,PE∥AB交BC于点E,PF∥AC交BC于点F,点P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.解:AD平分∠BAC.理由如下:∵D到PE的距离与到PF的距离相等,∴点D在∠EPF的平分线上.∴∠1=∠2.又∵PE∥AB,∴∠1=∠3.同理,∠2=∠4.∴∠3=∠4,∴AD平分∠BAC.P 3.已知:如图,OD平分∠POQ,在OP、OQ边上取OA=OB,点C在OD上,CM⊥AD于M,CN⊥BD于N.求证:CM=CN.证明:∵OD平分线∠POQ,∴∠AOD=∠BOD.在△AOD与△BOD中,∵OA=OB,∠AOD=∠BOD,OD=OD,∴△AOD≌△BOD.∴∠ADO=∠BDO.∵CM⊥AD,CN⊥BD,∴CM=CN.4.如图,已知∠CBD和∠BCE的平分线相交于点F,求证:点F在∠DAE的平分线上. 证明:过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M.∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC.∴FG=FM.又∵点F在∠CBD的平分线上, FH⊥AD, FM⊥BC,∴FM=FH,∴FG=FH.∴点F在∠DAE的平分线上. GHMABCFED拓展思维5.如图, 直线l1、l2、l3表示三条互相交叉的公路, 现要建一个货物中转站, 要求它到三条公路的距离相等, 可选择的地址有几处? 画出它的位置. P1P2P3P4l1l2l3小结 在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上。1、角平分线的判定:2、三角形角平分线的交点性质: 三角形的三条角平分线交于一点。3、角的平分线的辅助线作法:见角平分线就作两边垂线段。 教材第50页练习第1,2题; 教材第51页习题12.3第1,2,3题.布置作业
初中数学人教版八年级上册12.3 角的平分线的性质教课ppt课件: 这是一份初中数学人教版八年级上册12.3 角的平分线的性质教课ppt课件,共28页。PPT课件主要包含了角平分线的性质,知识回顾,学习目标,课堂导入,新知探究,跟踪训练,随堂练习,三角形全等的性质,角的平分线的判定,角平分线的判定等内容,欢迎下载使用。
数学12.3 角的平分线的性质课文ppt课件: 这是一份数学12.3 角的平分线的性质课文ppt课件,共14页。
初中人教版第十二章 全等三角形12.3 角的平分线的性质图文课件ppt: 这是一份初中人教版第十二章 全等三角形12.3 角的平分线的性质图文课件ppt,共28页。PPT课件主要包含了复习备用,几何语言,复习引入,学习目标,重点难点,新知探究,合作探究,归纳总结,学以致用,公共边等内容,欢迎下载使用。














