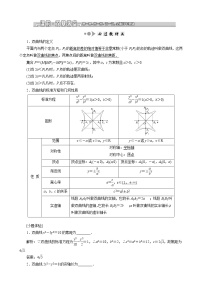
高中数学人教版新课标B选修2-12.5 直线与圆锥曲线教案设计

这是一份高中数学人教版新课标B选修2-12.5 直线与圆锥曲线教案设计，共25页。


直线与圆锥曲线的位置关系
判断直线l与圆锥曲线C的位置关系时，通常将直线l的方程Ax＋By＋C＝0(A，B不同时为0)代入圆锥曲线C的方程F(x，y)＝0，消去y(也可以消去x)得到一个关于变量x(或变量y)的一元方程．
即消去y，得ax2＋bx＋c＝0.
(1)当a≠0时，设一元二次方程ax2＋bx＋c＝0的判别式为Δ，则Δ＞0⇔直线与圆锥曲线C相交；
Δ＝0⇔直线与圆锥曲线C相切；
Δ＜0⇔直线与圆锥曲线C相离．
(2)当a＝0，b≠0时，即得到一个一次方程，则直线l与圆锥曲线C相交，且只有一个交点，此时，
若C为双曲线，则直线l与双曲线的渐近线的位置关系是平行；
若C为抛物线，则直线l与抛物线的对称轴的位置关系是平行或重合．
[小题体验]
1．若直线y＝kx与双曲线－＝1相交，则k的取值范围是________．
解析：双曲线－＝1的渐近线方程为y＝±x，若直线y＝kx与双曲线相交，数形结合得k∈.
答案：
2．已知椭圆C：＋＝1(a＞b＞0)，F(，0)为其右焦点，过点F且垂直于x轴的直线与椭圆相交所得的弦长为2，则椭圆C的方程为________．
解析：由题意得解得
所以椭圆C的方程为＋＝1.
答案：＋＝1




3．经过椭圆＋y2＝1的一个焦点作倾斜角为45°的直线l，交椭圆于A，B两点．设O为坐标原点，则·等于________．
解析：依题意，当直线l经过椭圆的右焦点(1,0)时，其方程为y－0＝tan 45°(x－1)，即y＝x－1，代入椭圆方程＋y2＝1并整理得3x2－4x＝0，解得x＝0或x＝，所以两个交点坐标分别为(0，－1)，，所以·＝－，同理，直线l经过椭圆的左焦点时，也可得·＝－.故·的值为－.
答案：－

1．直线与双曲线交于一点时，易误认为直线与双曲线相切，事实上不一定相切，当直线与双曲线的渐近线平行时，直线与双曲线相交于一点．
2．直线与抛物线交于一点时，除直线与抛物线相切外易忽视直线与对称轴平行时也相交于一点．
[小题纠偏]
1．过点(0,1)作直线，使它与抛物线y2＝4x仅有一个公共点，这样的直线有________条．
解析：结合图形分析可知，满足题意的直线共有3条：直线x＝0，过点(0,1)且平行于x轴的直线以及过点(0,1)且与抛物线相切的直线(非直线x＝0)．
答案：3
2．直线y＝x＋3与双曲线－＝1的交点有_______个．
解析：因为直线y＝x＋3与双曲线的渐近线y＝x平行，
所以它与双曲线只有1个交点．
答案：1

　
[典例引领]
已知椭圆C：＋＝1(a＞b＞0)的两个焦点分别为F1(－2,0)，F2(2,0)，离心率为.过点F2的直线l(斜率不为0)与椭圆C交于A，B两点，线段AB的中点为D，O为坐标原点，直线OD交椭圆于M，N两点．
(1)求椭圆C的方程；
(2)当四边形MF1NF2为矩形时，求直线l的方程．
解：(1)由题意可知解得a＝，b＝.
故椭圆C的方程为＋＝1.
(2)由题意可知直线l的斜率存在．设其方程为y＝k(x－2)，
点A(x1，y1)，B(x2，y2)，M(x3，y3)，N(－x3，－y3)，
由得(1＋3k2)x2－12k2x＋12k2－6＝0，
所以x1＋x2＝，
则y1＋y2＝k(x1＋x2－4)＝，
所以AB的中点D的坐标为，
因此直线OD的方程为x＋3ky＝0(k≠0)．
由解得y＝，x3＝－3ky3.
因为四边形MF1NF2为矩形，
所以·＝0，
即(x3－2，y3)·(－x3－2，－y3)＝0，
所以4－x－y＝0.
所以4－＝0.
解得k＝±.故直线l的方程为y＝±(x－2)．
[由题悟法]
1．直线与圆锥曲线位置关系的判定方法
(1)代数法：即联立直线与圆锥曲线方程可得到一个关于x，y的方程组，消去y(或x)得一元方程，此方程根的个数即为交点个数，方程组的解即为交点坐标．
(2)几何法：即画出直线与圆锥曲线的图象，根据图象判断公共点个数．
2．判定直线与圆锥曲线位置关系的注意点
(1)联立直线与圆锥曲线的方程消元后，应注意讨论二次项系数是否为零的情况．
(2)判断直线与圆锥曲线位置关系时，判别式Δ起着关键性的作用，第一：可以限定所给参数的范围；第二：可以取舍某些解以免产生增根．




[即时应用]
　(2019·泰州中学高三学情调研) 已知椭圆的离心率为，焦距为2，直线y＝kx(x≠0)与椭圆C交于A，B两点，M为其右准线与x轴的交点，直线AM，BM分别与椭圆C交于A1，B1两点，记直线A1B1的斜率为k1.
(1)求椭圆C的方程；
(2)是否存在常数λ，使得k1＝λk恒成立？若存在，求出λ的值；若不存在，请说明理由．
解：(1)设椭圆方程为＋＝1(a＞b＞0)，
由椭圆的焦距2c＝2，得c＝1.
由椭圆的离心率e＝＝，得a＝，
则b2＝a2－c2＝1，
所以椭圆C的方程为＋y2＝1.
(2)设A(x0，y0)，则B(－x0，－y0)，k＝，2y＝2－x，又右准线方程为x＝2，则M(2,0)，直线AM的方程为y＝(x－2)，
联立消去y，整理得[(x0－2)2＋2y]x2－8yx＋8y－2(x0－2)2＝0，
因为方程的两个根为x0，xA1，
所以x0·xA1＝＝＝·x0，
则xA1＝，yA1＝(xA1－2)＝，
则A1，同理可得B1，则k1＝－＝－3k，
即存在λ＝－3，使得k1＝λk恒成立．
　
[典例引领]
(2017·全国卷Ⅰ)已知椭圆C：＋＝1(a＞b＞0)，四点P1(1,1)，P2(0，1)，P3，P4中恰有三点在椭圆C上．
(1)求C的方程；
(2)设直线l不经过P2点且与C相交于A，B两点．若直线P2A与直线P2B的斜率的和为－1，证明：l过定点．
解：(1)由于P3，P4两点关于y轴对称，
故由题设知椭圆C经过P3，P4两点．
又由＋＞＋知，椭圆C不经过点P1，
所以点P2在椭圆C上．
因此解得
故椭圆C的方程为＋y2＝1.
(2)证明：设直线P2A与直线P2B的斜率分别为k1，k2.
如果l与x轴垂直，设l：x＝t，由题设知t≠0，且|t|＜2，可得A，B的坐标分别为，.
则k1＋k2＝－＝－1，得t＝2，不符合题设．
从而可设l：y＝kx＋m(m≠1)．
将y＝kx＋m代入＋y2＝1得
(4k2＋1)x2＋8kmx＋4m2－4＝0.
由题设可知Δ＝16(4k2－m2＋1)＞0.
设A(x1，y1)，B(x2，y2)，
则x1＋x2＝－，x1x2＝.
而k1＋k2＝＋
＝＋
＝.
由题设k1＋k2＝－1，
故(2k＋1)x1x2＋(m－1)(x1＋x2)＝0.
即(2k＋1)·＋(m－1)·＝0.
解得k＝－.
当且仅当m＞－1时，Δ＞0，于是l：y＝－x＋m，即y＋1＝－(x－2)，
所以l过定点(2，－1)．
[由题悟法]
定点、定值问题的求解策略
(1)定点问题的求解策略
把直线或曲线方程中的变量x，y当作常数看待，把方程一端化为零，既然直线或曲线过定点，那么这个方程就要对任意参数都成立，这时参数的系数就要全部等于零，这样就得到一个关于x，y的方程组，这个方程组的解所确定的点就是直线或曲线所过的定点．
(2)定值问题的求解策略
在解析几何中，有些几何量与参数无关，这就是“定值”问题，解决这类问题常通过取特殊值，先确定“定值”是多少，再进行证明，或者将问题转化为代数式，再证明该式是与变量无关的常数或者由该等式与变量无关，令其系数等于零即可得到定值．
[即时应用]
　(2019·徐州一模)已知中心在原点，对称轴为坐标轴的椭圆C的一个焦点F在抛物线y2＝4x的准线上，且椭圆C过点P，直线l与椭圆C交于A，B两点．
(1)求椭圆C的方程；
(2)若直线l的斜率为，且不过点P，设直线PA，PB的斜率分别为k1，k2，求证：k1＋k2为定值．
解：(1)抛物线y2＝4x的准线方程为x＝－1，由题意知F(－1,0)．
设椭圆C的方程为＋＝1(a＞b＞0)．
则由题意可得解得
故椭圆C的方程为＋＝1.
(2)证明：因为直线l的斜率为，且不过点P，
所以可设直线l的方程为y＝x＋m(m≠1)．
联立方程组消去y得x2＋mx＋m2－3＝0.设A(x1，y1)，B(x2，y2)，
故有
所以k1＋k2＝＋
＝
＝
＝
＝＝0，
所以k1＋k2为定值0.
　
[典例引领]
　(2018·苏北四市期末)如图，在平面直角坐标系xOy中，已知椭圆C：＋＝1(a＞b＞0)的离心率为，且右焦点F到左准线的距离为6.
(1)求椭圆C的标准方程；
(2)设A为椭圆C的左顶点，P为椭圆C上位于x轴上方的点，直线PA交y轴于点M，过点F作MF的垂线，交y轴于点N.
①当直线PA的斜率为时，求△FMN的外接圆的方程；
②设直线AN交椭圆C于另一点Q，求△APQ的面积的最大值．
解：(1)由题意得解得则b＝2，
所以椭圆C的方程为＋＝1.
(2)由题意可设直线PA的方程为y＝k(x＋4)，k＞0，则M(0，4k)，
所以kMF＝＝－k，kFN＝，
所以直线FN的方程为y＝(x－2)，则N.
①当直线PA的斜率为，即k＝时，M(0,2)，N(0，－4)，F(2，0)，
因为MF⊥FN，所以圆心为(0，－1)，半径为3，
所以△FMN的外接圆的方程为x2＋(y＋1)2＝9.
②联立消去y，整理得(1＋2k2)x2＋16k2x＋32k2－16＝0，
解得x1＝－4或x2＝，所以P，
又直线AN的方程为y＝－(x＋4)，
同理可得，Q，
所以P，Q关于原点对称，即PQ过原点．
所以△APQ的面积S＝OA·(yP－yQ)＝2×＝≤8，
当且仅当2k＝，即k＝时取“＝”．
所以△APQ的面积的最大值为8.
[由题悟法]
圆锥曲线中的最值问题解决方法
(1)代数法：从代数的角度考虑，通过建立函数、不等式等模型，利用二次函数法和基本不等式法、换元法、导数法等方法求最值．
(2)几何法：从圆锥曲线的几何性质的角度考虑，根据圆锥曲线几何意义求最值．
[即时应用]
　已知椭圆＋＝1(a＞b＞0)的离心率为，且经过点P，过它的两个焦点F1，F2分别作直线l1与l2，l1交椭圆于A，B两点，l2交椭圆于C，D两点，且l1⊥l2.
(1)求椭圆的标准方程；
(2)求四边形ABCD的面积S的取值范围．
解：(1)由＝，得a＝2c，所以a2＝4c2，b2＝3c2，
将点P的坐标代入椭圆方程得c2＝1，
故所求椭圆方程为＋＝1.
(2)若l1与l2中有一条直线的斜率不存在，则另一条直线的斜率为0，此时四边形的面积为S＝6.
若l1与l2的斜率都存在，设l1的斜率为k，则l2的斜率为－.
不妨设直线l1的方程为y＝k(x＋1)，
设A(x1，y1)，B(x2，y2)，
联立
消去y整理得，(4k2＋3)x2＋8k2x＋4k2－12＝0，
Δ＝64k4－4(3＋4k2)(4k2－12)＝144k2＋144＞0，
所以x1＋x2＝－，x1·x2＝，
所以|x1－x2|＝＝，
所以AB＝|x1－x2|＝，
同理可得CD＝，
所以S＝AB·CD＝，
令k2＝t∈(0，＋∞)，
所以S＝
＝
＝6－
≥6－＝，
所以S∈.
综上可知，四边形ACBD面积的取值范围是.

一保高考，全练题型做到高考达标
1．(2019·徐州第一中学检测)若双曲线－＝1与直线y＝kx－1有且仅有一个公共点，则这样的直线有______条．
解析：把直线y＝kx－1代入双曲线－＝1中，
消去y，得(4－9k2)x2＋18kx－45＝0，
当4－9k2＝0，即k＝±时，直线与双曲线相交，有一个交点；
当4－9k2≠0，即k≠±时，令Δ＝0，
得182k2＋4(4－9k2)×45＝0，解得k＝±，此时直线与双曲线相切，有一个交点．
综上，k的值有4个，即这样的直线有4条．
答案：4
2．已知椭圆C：＋＝1的左、右顶点分别为M，N，点P在C上，且直线PN的斜率是－，则直线PM的斜率为________．
解析：设P(x0，y0)，则＋＝1，直线PM的斜率kPM＝，直线PN的斜率kPN＝，可得kPM·kPN＝＝－，故kPM＝－·＝3.
答案：3
3．已知抛物线y2＝2px的焦点F与椭圆16x2＋25y2＝400的左焦点重合，抛物线的准线与x轴的交点为K，点A在抛物线上且AK＝AF，则点A的横坐标为________．
解析：16x2＋25y2＝400可化为＋＝1，
则椭圆的左焦点为F(－3,0)，
又抛物线y2＝2px的焦点为，准线为x＝－，
所以＝－3，即p＝－6，即y2＝－12x，K(3,0)．
设A(x，y)，则由AK＝AF得
(x－3)2＋y2＝2[(x＋3)2＋y2]，即x2＋18x＋9＋y2＝0，
又y2＝－12x，所以x2＋6x＋9＝0，解得x＝－3.
答案：－3
4．(2019·江都中学检测)已知双曲线－＝1(a＞0，b＞0)的两条渐近线与抛物线y2＝2px(p＞0)的准线分别交于A，B两点，若双曲线的离心率为2，O为坐标原点，△AOB的面积为，则p＝________.
解析：∵双曲线－＝1的渐近线方程是y＝±x，
抛物线y2＝2px(p＞0)的准线方程是x＝－，
∴A，B两点的纵坐标分别是y＝±，
∵双曲线的离心率为2，
∴＝＝e2－1＝3，则＝，
∴A，B两点的纵坐标分别是y＝±＝±，
又△AOB的面积为，
∴×p×＝，解得p＝.
答案：
5．已知(4,2)是直线l被椭圆＋＝1所截得的线段的中点，则l的方程是___________．
解析：设直线l与椭圆相交于A(x1，y1)，B(x2，y2)．
则＋＝1，且＋＝1，
两式相减并化简得＝－.
又x1＋x2＝8，y1＋y2＝4，
所以＝－，
故直线l的方程为y－2＝－(x－4)，
即x＋2y－8＝0.
答案：x＋2y－8＝0
6．(2018·海门中学检测)如图，过抛物线y＝x2的焦点F的直线l与抛物线和圆x2＋(y－1)2＝1交于A，B，C，D四点，则·＝________.

解析：不妨设直线AB的方程为y＝1，联立解得x＝±2，则A(－2,1)，D(2,1)，因为B(－1,1)，C(1,1)，所以＝(1,0)，＝(－1,0)，所以·＝－1.
答案：－1
7．(2019·宁海中学调研)已知椭圆＋＝1(a＞b＞0)，点A，B1，B2，F依次为其左顶点、下顶点、上顶点和右焦点，若直线AB2与直线B1F的交点恰在椭圆的右准线上，则椭圆的离心率为________．
解析：根据题意得，直线AB2的方程为：y＝x＋b，
直线B1F的方程为：y＝x－b，
联立两直线方程解得x＝.
又由题意可得＝，
化简得2c2＋ac－a2＝0，
即2e2＋e－1＝0，
又0＜e＜1，解得e＝.
答案：
8．已知直线l过抛物线C：y2＝2px(p＞0)的焦点，且与抛物线的对称轴垂直，直线l与抛物线C交于A，B两点，且AB＝12，若M为抛物线C的准线上一点，则△ABM的面积为________．
解析：由题意知，抛物线C的焦点坐标为，对称轴为x轴，准线为x＝－.因为直线l与x轴垂直，所以AB＝2p＝12，p＝6，又点M在抛物线C的准线上，所以点M到直线AB的距离为6，所以△ABM的面积S＝×6×12＝36.
答案：36
9．(2018·镇江期末)已知椭圆C：＋＝1(a＞b＞0)的离心率为，且点在椭圆C上．
(1)求椭圆C的方程；
(2)若直线l交椭圆C于P，Q两点，线段PQ的中点为H，O为坐标原点，且OH＝1，求△POQ面积的最大值．
解：(1)由已知得解得
所以椭圆C的方程为＋y2＝1.
(2)设l与x轴的交点为D(n,0)，直线l：x＝my＋n，P(x1，y1)，Q(x2，y2)，
联立消去x，整理得(4＋m2)y2＋2mny＋n2－4＝0，
所以y1＋y2＝－，y1y2＝，
故＝－，＝＝，
即H，
由OH＝1，得n2＝，
则S△POQ＝OD|y1－y2|＝|n||y1－y2|.
令T＝n2(y1－y2)2＝n2[(y1＋y2)2－4y1y2]＝，
设t＝4＋m2(t≥4)，则＝＝≤＝，
当且仅当t＝，即t＝12时，S△POQ＝1，
所以△POQ面积的最大值为1.
10.如图，在平面直角坐标系xOy中，过椭圆C：＋y2＝1的左顶点A作直线l，与椭圆C和y轴正半轴分别交于点P，Q.
(1)若AP＝PQ，求直线l的斜率；
(2)过原点O作直线l的平行线，与椭圆C交于点M，N，求证：为定值．
解：(1)依题意，椭圆C的左顶点A(－2,0)，
设直线l的斜率为k(k＞0)，点P的横坐标为xP，
则直线l的方程为y＝k(x＋2)．
联立得(4k2＋1)x2＋16k2x＋16k2－4＝0，
则－2·xP＝，从而xP＝.
因为AP＝PQ，所以xP＝－1.
所以＝－1，解得k＝(负值舍去)．

(2)证明：设点N的横坐标为xN.结合(1)知，直线MN的方程为y＝kx.
联立得x＝.
从而＝＝＝(定值)．
二上台阶，自主选做志在冲刺名校
1．(2019·苏州调研)如图，在平面直角坐标系xOy中，椭圆C：＋＝1(a＞b＞0)的离心率为，椭圆上的动点P到一个焦点的距离的最小值为3(－1)．
(1)求椭圆C的标准方程；
(2)已知过点M(0，－1)的动直线l与椭圆C交于A，B两点，试判断以线段AB为直径的圆是否恒过定点，并说明理由．
解：(1)由题意得＝，故a＝c.
又椭圆上的动点P到一个焦点的距离的最小值为3(－1)，
所以a－c＝3(－1)，
所以c＝3，a＝3，所以b2＝a2－c2＝9，
所以椭圆C的标准方程为＋＝1.
(2)当直线l的斜率为0时，对于＋＝1，令y＝－1，得x＝±4，
此时以线段AB为直径的圆的方程为x2＋(y＋1)2＝16.
当直线l的斜率不存在时，以线段AB为直径的圆的方程为x2＋y2＝9.
联立解得即两圆的交点为(0,3)，记T(0,3)．
猜想以线段AB为直径的圆恒过定点T(0,3)．
当直线l的斜率存在且不为0时，设直线l的方程为y＝kx－1(k≠0)，A(x1，y1)，B(x2，y2)，
由得(1＋2k2)x2－4kx－16＝0，
所以Δ＝(－4k)2＋64(1＋2k2)＝144k2＋64＞0，x1＋x2＝，x1x2＝－.
因为·TB―→＝(x1，y1－3)·(x2，y2－3)＝x1x2＋y1y2－3(y1＋y2)＋9＝x1x2＋(kx1－1)(kx2－1)－3(kx1－1＋kx2－1)＋9＝(k2＋1)x1x2－4k(x1＋x2)＋16＝－＋16＝＋16＝0，所以TA⊥TB，故以线段AB为直径的圆过点T(0,3)．
综上，以线段AB为直径的圆恒过定点(0,3)．
2．(2019·盐城模拟)如图，已知F1，F2分别是椭圆C：＋＝1(a＞b＞0)的左、右焦点，点P(－2,3)是椭圆C上一点，且PF1⊥x轴．
(1)求椭圆C的方程；
(2)设圆M：(x－m)2＋y2＝r2(r＞0)．
①设圆M与线段PF2交于A，B两点，若＋＝＋，且AB＝2，求r的值；
②设m＝－2，过点P作圆M的两条切线分别交椭圆C于G，H两点(均异于点P)．试问：是否存在这样的正数r，使得G，H两点恰好关于坐标原点O对称？若存在，求出r的值；若不存在，请说明理由．
解：(1)因为点P(－2,3)是椭圆C上一点，且PF1⊥x轴，
所以椭圆的半焦距c＝2，
由＋＝1，得y＝±，所以＝＝3，
化简得a2－3a－4＝0，解得a＝4，所以b2＝12，
所以椭圆C的方程为＋＝1.
(2)①因为＋＝＋，
所以－＝－，即＝.
所以线段PF2与线段AB的中点重合(记为点Q)，
由(1)知Q.
因为圆M与线段PF2交于A，B两点，
所以kMQ·kAB＝kMQ·kPF2＝－1，
即·＝－1，解得m＝－，
所以MQ＝ ＝，
又AB＝2，所以r＝ ＝.
②假设存在正数r满足题意．
由G，H两点恰好关于原点对称，设G(x0，y0)，则H(－x0，－y0)，不妨设x0＜0.
因为P(－2,3)，m＝－2，所以两条切线的斜率均存在，
设过点P与圆M相切的直线的斜率为k，
则切线方程为y－3＝k(x＋2)，即kx－y＋2k＋3＝0，
由该直线与圆M相切，得r＝，即k＝± ，
所以两条切线的斜率互为相反数，即kPG＝－kPH，
所以＝－，化简得x0y0＝－6，即y0＝，
代入＋＝1，化简得x－16x＋48＝0，
解得x0＝－2(舍去)或x0＝－2，
所以y0＝，
所以G(－2，)，H(2，－)，
所以kPG＝＝，
所以r＝＝.
故存在满足条件的正数r，且r＝.

命题点一　椭圆
1.(2018·浙江高考)已知点P(0,1)，椭圆＋y2＝m(m＞1)上两点A，B满足＝2，则当m＝________时，点B横坐标的绝对值最大．
解析：设A(x1，y1)，B(x2，y2)，由＝2，
得即x1＝－2x2，y1＝3－2y2.
因为点A，B在椭圆上，所以
解得y2＝m＋，
所以x＝m－(3－2y2)2＝－m2＋m－＝－(m－5)2＋4≤4，
所以当m＝5时，点B横坐标的绝对值最大．
答案：5
2．(2016·江苏高考)如图，在平面直角坐标系xOy中，F是椭圆＋＝1(a＞b＞0)的右焦点，直线y＝与椭圆交于B，C两点，且∠BFC＝90°，则该椭圆的离心率是________．
解析：将y＝代入椭圆的标准方程，得＋＝1，
所以x＝±a，故B，C.
又因为F(c,0)，所以＝，＝.
因为∠BFC＝90°，所以·＝0，
所以＋2＝0，
即c2－a2＋b2＝0，
将b2＝a2－c2代入并化简，得a2＝c2，
所以e2＝＝，所以e＝(负值舍去)．
答案：
3．(2017·江苏高考)如图，在平面直角坐标系xOy中，椭圆E：＋＝1(a＞b＞0)的左、右焦点分别为F1，F2，离心率为，两准线之间的距离为8.点P在椭圆E上，且位于第一象限，过点F1作直线PF1的垂线l1，过点F2作直线PF2的垂线l2.
(1)求椭圆E的标准方程；
(2)若直线l1，l2的交点Q在椭圆E上，求点P的坐标．
解：(1)设椭圆的半焦距为c.
因为椭圆E的离心率为，两准线之间的距离为8，
所以＝，＝8，
解得a＝2，c＝1，于是b＝＝，
因此椭圆E的标准方程是＋＝1.
(2)由(1)知，F1(－1,0)，F2(1,0)．
设P(x0，y0)，因为P为第一象限的点，
故x0＞0，y0＞0.
当x0＝1时，l2与l1相交于F1，与题设不符．
当x0≠1时，直线PF1的斜率为，直线PF2的斜率为.
因为l1⊥PF1，l2⊥PF2，所以直线l1的斜率为－，直线l2的斜率为－，
从而直线l1的方程为y＝－(x＋1)， ①
直线l2的方程为y＝－(x－1)． ②
由①②，解得x＝－x0，y＝，
所以Q.
因为点Q在椭圆上，由对称性，得＝±y0，
即x－y＝1或x＋y＝1.
又点P在椭圆E上，故＋＝1.
联立解得
联立无解．
因此点P的坐标为.
4．(2018·北京高考)已知椭圆M：＋＝1(a＞b＞0)的离心率为，焦距为2.斜率为k的直线l与椭圆M有两个不同的交点A，B.
(1)求椭圆M的方程；
(2)若k＝1，求|AB|的最大值；
(3)设P(－2,0)，直线PA与椭圆M的另一个交点为C，直线PB与椭圆M的另一个交点为D，若C，D和点Q共线，求k.
解：(1)由题意得解得a＝，b＝1.
所以椭圆M的方程为＋y2＝1.
(2)设直线l的方程为y＝x＋m，A(x1，y1)，B(x2，y2)．
由得4x2＋6mx＋3m2－3＝0，
所以x1＋x2＝－，x1x2＝.
所以|AB|＝
＝＝＝ .
当m＝0，即直线l过原点时，|AB|最大，最大值为.
(3)设A(x1，y1)，B(x2，y2)，
由题意得x＋3y＝3，x＋3y＝3.
直线PA的方程为y＝(x＋2)．
由得[(x1＋2)2＋3y]x2＋12yx＋12y－3(x1＋2)2＝0.
设C(xC，yC)，所以xC＋x1＝＝.
所以xC＝－x1＝.
所以yC＝(xC＋2)＝.
设D(xD，yD)，
同理得xD＝，yD＝.
记直线CQ，DQ的斜率分别为kCQ，kDQ，
则kCQ－kDQ＝－＝4(y1－y2－x1＋x2)．
因为C，D，Q三点共线，所以kCQ－kDQ＝0.
故y1－y2＝x1－x2.
所以直线l的斜率k＝＝1.
5．(2017·天津高考)已知椭圆＋＝1(a＞b＞0)的左焦点为F(－c,0)，右顶点为A，点E的坐标为(0，c), △EFA的面积为.
(1)求椭圆的离心率；
(2)设点Q在线段AE上，|FQ|＝c，延长线段FQ与椭圆交于点P，点M，N在x轴上，PM∥QN，且直线PM与直线QN间的距离为c，四边形PQNM的面积为3c.
①求直线FP的斜率；
②求椭圆的方程．
解：(1)设椭圆的离心率为e.
由已知，可得(c＋a)c＝.
又由b2＝a2－c2，
可得2c2＋ac－a2＝0，即2e2＋e－1＝0.
又因为0＜e＜1，解得e＝.
所以椭圆的离心率为.
(2)①依题意，设直线FP的方程为x＝my－c(m＞0)，
则直线FP的斜率为.
由(1)知a＝2c，可得直线AE的方程为＋＝1，
即x＋2y－2c＝0，与直线FP的方程联立，
可解得x＝，y＝，
即点Q的坐标为.
由已知|FQ|＝c，有2＋2＝2，整理得3m2－4m＝0，所以m＝，即直线FP的斜率为.
②由a＝2c，可得b＝c，
故椭圆方程可以表示为＋＝1.
由①得直线FP的方程为3x－4y＋3c＝0，
联立消去y，整理得7x2＋6cx－13c2＝0，
解得x＝c或x＝－(舍去)．
因此可得点P，
进而可得|FP|＝ ＝，
所以|PQ|＝|FP|－|FQ|＝－＝c.
由已知，线段PQ的长即为PM与QN这两条平行直线间的距离，
故直线PM和QN都垂直于直线FP.
因为QN⊥FP，
所以|QN|＝|FQ|·tan∠QFN＝×＝，
所以△FQN的面积为|FQ||QN|＝，
同理，△FPM的面积等于，
由四边形PQNM的面积为3c，
得－＝3c，整理得c2＝2c.
又由c＞0，得c＝2.
所以椭圆的方程为＋＝1.

命题点二　双曲线
1.(2018·江苏高考)在平面直角坐标系xOy中，若双曲线－＝1(a＞0，b＞0)的右焦点F(c,0)到一条渐近线的距离为c，则其离心率的值为________．
解析：∵双曲线的渐近线方程为bx±ay＝0，
∴焦点F(c,0)到渐近线的距离d＝＝b，
∴b＝c，∴a＝＝c，
∴e＝＝2.
答案：2
2．(2016·江苏高考)在平面直角坐标系xOy中，双曲线－＝1的焦距是________．
解析：由双曲线的标准方程，知a2＝7，b2＝3，所以c2＝a2＋b2＝10，
所以c＝，从而焦距2c＝2.
答案：2
3．(2017·江苏高考)在平面直角坐标系xOy中，双曲线－y2＝1的右准线与它的两条渐近线分别交于点P，Q，其焦点是F1，F2，则四边形F1PF2Q的面积是________．
解析：由题意得，双曲线的右准线x＝与两条渐近线y＝±x的交点坐标为.
不妨设双曲线的左、右焦点分别为F1，F2，
则F1(－2,0)，F2(2,0)，
故四边形F1PF2Q的面积是
|F1F2|·|PQ|＝×4×＝2.
答案：2
4．(2018·北京高考)若双曲线－＝1(a＞0)的离心率为，则a＝________.
解析：由e＝＝ ，得＝，
∴a2＝16.
∵a＞0，∴a＝4.
答案：4
5．(2018·全国卷Ⅲ改编)设F1，F2是双曲线C：－＝1(a＞0，b＞0)的左、右焦点，O是坐标原点．过F2作C的一条渐近线的垂线，垂足为P.若|PF1|＝|OP|，则C的离心率为________．
解析：法一：不妨设一条渐近线的方程为y＝x，
则F2到y＝x的距离d＝＝b.
在Rt△F2PO中，|F2O|＝c，
所以|PO|＝a，所以|PF1|＝a，
又|F1O|＝c，所以在△F1PO与Rt△F2PO中，
根据余弦定理得
cos∠POF1＝＝－cos∠POF2＝－，
即3a2＋c2－(a)2＝0，得3a2＝c2，所以e＝＝.
法二：如图，过点F1向OP的反向延长线作垂线，垂足为P′，连接P′F2，由题意可知，四边形PF1P′F2为平行四边形，且 △PP′F2是直角三角形．因为|F2P|＝b，|F2O|＝c，所以|OP|＝a.
又|PF1|＝a＝|F2P′|，|PP′|＝2a，所以|F2P|＝a＝b，所以c＝＝a，所以e＝＝.
答案：
6．(2015·江苏高考)在平面直角坐标系xOy中，P为双曲线x2－y2＝1右支上的一个动点，若点P到直线x－y＋1＝0的距离大于c恒成立，则实数c的最大值为________．
解析：所求的c的最大值就是双曲线的一条渐近线x－y＝0与直线x－y＋1＝0的距离，此距离d＝＝.
答案：
命题点三　抛物线
1.(2017·全国卷Ⅱ改编)过抛物线C：y2＝4x的焦点F，且斜率为的直线交C于点M(M在x轴的上方)，l为C的准线，点N在l上且MN⊥l，则M到直线NF的距离为________．
解析：法一：由题意，得F(1,0)，
则直线FM的方程是y＝(x－1)．
由得x＝或x＝3.
由M在x轴的上方，得M(3,2)，
由MN⊥l，得|MN|＝|MF|＝3＋1＝4.
又∠NMF等于直线FM的倾斜角，即∠NMF＝60°，
因此△MNF是边长为4的等边三角形，
所以点M到直线NF的距离为4×＝2.
法二：依题意，得直线FM的倾斜角为60°，
则|MN|＝|MF|＝＝4.
又∠NMF等于直线FM的倾斜角，即∠NMF＝60°，
因此△MNF是边长为4的等边三角形，
所以点M到直线NF的距离为4×＝2.
答案：2
2．(2018·北京高考)已知直线l过点(1,0)且垂直于x轴，若l被抛物线y2＝4ax截得的线段长为4，则抛物线的焦点坐标为________．
解析：由题知直线l的方程为x＝1，则直线与抛物线的交点为(1，±2)(a＞0)．
又直线被抛物线截得的线段长为4，
所以4＝4，即a＝1.
所以抛物线的焦点坐标为(1,0)．
答案：(1,0)
3．(2017·天津高考)设抛物线y2＝4x的焦点为F，准线为l.已知点C在l上，以C为圆心的圆与y轴的正半轴相切于点A.若∠FAC＝120°，则圆的方程为________________．
解析：由题意知该圆的半径为1，
设圆心坐标为C(－1，a)(a＞0)，则A(0，a)．
又F(1,0)，所以＝(－1,0)，＝(1，－a)，
由题意得与的夹角为120°，
故cos 120°＝＝－，解得a＝，
所以圆的方程为(x＋1)2＋(y－)2＝1.
答案：(x＋1)2＋(y－)2＝1
4．(2017·浙江高考)如图，已知抛物线x2＝y，点A，B，抛物线上的点P(x，y).过点B作直线AP的垂线，垂足为Q.
(1)求直线AP斜率的取值范围；
(2)求|PA|·|PQ|的最大值．
解：(1)设直线AP的斜率为k，k＝＝x－，
因为－＜x＜，
所以直线AP斜率的取值范围是(－1,1)．
(2)设直线AP的斜率为k，则直线BQ的斜率为－.
则直线AP的方程为y－＝k，
即kx－y＋k＋＝0，
直线BQ的方程为y－＝－，
即x＋ky－k－＝0，
联立
解得点Q的横坐标xQ＝.
因为|PA|＝ ＝ (k＋1)，|PQ|＝(xQ－x)＝－，
所以|PA|·|PQ|＝－(k－1)(k＋1)3.
令f(k)＝－(k－1)(k＋1)3，
因为f′(k)＝－(4k－2)(k＋1)2，
所以f(k)在区间上单调递增，上单调递减，
因此当k＝时，|PA|·|PQ|取得最大值.
命题点四　圆锥曲线中的综合问题
1．(2018·江苏高考)如图，在平面直角坐标系xOy中，椭圆C过点，焦点为F1(－，0)，F2(，0)，圆O的直径为F1F2.
(1)求椭圆C及圆O的方程；
(2)设直线l与圆O相切于第一象限内的点P.
①若直线l与椭圆C有且只有一个公共点，求点P的坐标；
②直线l与椭圆C交于A，B两点．若△OAB的面积为，求直线l的方程．
解：(1)因为椭圆C的焦点为F1(－，0)，F2(，0)，
可设椭圆C的方程为＋＝1(a＞b＞0)．
又点在椭圆C上，
所以解得
所以椭圆C的方程为＋y2＝1.
因为圆O的直径为F1F2，
所以圆O的方程为x2＋y2＝3.
(2)①设直线l与圆O相切于点P(x0，y0)(x0＞0，y0＞0)，则x＋y＝3，
所以直线l的方程为y＝－(x－x0)＋y0，
即y＝－x＋.
由消去y，得(4x＋y)x2－24x0x＋36－4y＝0.(*)
因为直线l与椭圆C有且只有一个公共点，
所以Δ＝(－24x0)2－4(4x＋y)·(36－4y)＝48y(x－2)＝0.
因为x0＞0，y0＞0，所以x0＝，y0＝1.
所以点P的坐标为(，1)．
②因为△OAB的面积为，
所以AB·OP＝，从而AB＝.
设A(x1，y1)，B(x2，y2)，
由(*)得x1,2＝，
所以AB2＝(x1－x2)2＋(y1－y2)2＝·.
因为x＋y＝3，
所以AB2＝＝，
即2x－45x＋100＝0，
解得x＝(x＝20舍去)，则y＝，
因此P的坐标为.
所以直线l的方程为y－＝－，
即y＝－x＋3.
2．(2017·天津高考)设椭圆＋＝1(a＞b＞0)的左焦点为F，右顶点为A，离心率为.已知A是抛物线y2＝2px(p＞0)的焦点，F到抛物线的准线l的距离为.
(1)求椭圆的方程和抛物线的方程；
(2)设l上两点P，Q关于x轴对称，直线AP与椭圆相交于点B(B异于点A)，直线BQ与x轴相交于点D.若△APD的面积为，求直线AP的方程．
解：(1)设点F的坐标为(－c,0)，
依题意解得
于是b2＝a2－c2＝.
所以椭圆的方程为x2＋＝1，抛物线的方程为y2＝4x.
(2)设直线AP的方程为x＝my＋1(m≠0)，与直线l的方程x＝－1联立，
可得点P，故点Q.
联立消去x，
整理得(3m2＋4)y2＋6my＝0，
解得y＝0或y＝.
由点B异于点A，可得点B.
由Q，可得直线BQ的方程为
(x＋1)－＝0，
令y＝0，解得x＝，故点D.
所以|AD|＝1－＝.
又因为△APD的面积为，
故××＝，
整理得3m2－2|m|＋2＝0，解得|m|＝，
所以m＝±.
所以直线AP的方程为3x＋y－3＝0或3x－y－3＝0.