人教版新课标B选修4-5排序不等式教案设计
展开一、教学目标
1.了解排序不等式的数学思想和背景.
2.理解排序不等式的结构与基本原理,会用排序不等式解决简单的不等式问题.
二、课时安排
1课时
三、教学重点
1.了解排序不等式的数学思想和背景.
2.理解排序不等式的结构与基本原理,会用排序不等式解决简单的不等式问题.
四、教学难点
1.了解排序不等式的数学思想和背景.
2.理解排序不等式的结构与基本原理,会用排序不等式解决简单的不等式问题.
五、教学过程
(一)导入新课
某班学生要开联欢会,需要买价格不同的礼品4件,5件和2件.现在选择商店中单价分别为3元,2元和1元的礼品,则至少要花________元,最多要花________元.
【解析】 取两组实数(2,4,5)和(1,2,3),则顺序和为2×1+4×2+5×3=25,反序和为2×3+4×2+5×1=19.
所以最少花费为19元,最多花费为25元.
【答案】 19 25
(二)讲授新课
教材整理1 顺序和、乱序和、反序和的概念
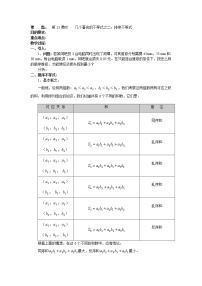
设a1≤a2≤a3≤…≤an,b1≤b2≤b3≤…≤bn为两组实数,c1,c2,…,cn是b1,b2,…,bn的任一排列,则称ai与bi(i=1,2,…,n)的相同顺序相乘所得积的和 为顺序和,和 为乱序和,相反顺序相乘所得积的和 称为反序和.
教材整理2 排序不等式
设a1≤a2≤…≤an,b1≤b2≤…≤bn为两组实数,c1,c2,…,cn是b1,b2,…,bn的任一排列,则 ≤ ≤ ,当且仅当a1=a2=…=an或b1=b2=…=bn时,反序和等于顺序和,此不等式简记为 ≤ ≤顺序和.
(三)重难点精讲
题型一、用排序不等式证明不等式(字母大小已定)
例1已知a,b,c为正数,a≥b≥c,求证:
(1)≥≥;
(2)++≥++.
【精彩点拨】 由于题目条件中已明确a≥b≥c,故可以直接构造两个数组.
【自主解答】 (1)∵a≥b>0,于是≤.
又c>0,∴>0,从而≥,
同理,∵b≥c>0,于是≤,
∴a>0,∴>0,于是得≥,
从而≥≥.
(2)由(1)知≥≥>0且a≥b≥c>0,
∴≥≥,a2≥b2≥c2.
由排序不等式,顺序和≥乱序和得
++≥++=++=++,
故++≥++.
规律总结:利用排序不等式证明不等式的技巧在于仔细观察、分析所要证明的式子的结构,从而正确地构造出不等式中所需要的带有大小顺序的两个数组.
[再练一题]
1.本例题中条件不变,求证:++≥++.
【证明】 ∵a≥b≥c≥0,
∴a5≥b5≥c5,
≥≥>0.
∴≥≥,
∴≥≥,由顺序和≥乱序和得
++≥++
=++,
∴++≥++.
题型二、字母大小顺序不定的不等式证明
例2设a,b,c为正数,求证:++≤++.
【精彩点拨】 (1)题目涉及到与排序有关的不等式;
(2)题目中没有给出a,b,c的大小顺序.解答本题时不妨先设定a≤b≤c,再利用排序不等式加以证明.
【自主解答】 不妨设0<a≤b≤c,则a3≤b3≤c3,
0<≤≤,
由排序原理:乱序和≤顺序和,得
a3·+b3·+c3·≤a3·+b3·+c3·,
a3·+b3·+c3·≤a3·+b3·+c3·.
将上面两式相加得
++≤2,
将不等式两边除以2,
得++≤++.
规律总结:在排序不等式的条件中需要限定各数值的大小关系,对于没有给出大小关系的情况:(1)要根据各字母在不等式中地位的对称性,限定一种大小关系.(2)若给出的字母不具有对称性,一定不能直接限定字母的大小顺序,而要根据具体环境分类讨论.
[再练一题]
2.设a1,a2,…,an为正数,求证:++…++≥a1+a2+…+an.
【证明】 不妨设0<a1≤a2≤…≤an,则
a≤a≤…≤a,≥≥…≥.
由排序不等式知,乱序和不小于反序和,所以
++…++≥a·+a·+…+a·,即
++…++≥a1+a2+…+an.
题型三、利用排序不等式求最值
例3 设A,B,C表示△ABC的三个内角,a,b,c表示其对边,求的最小值(A,B,C用弧度制表示).
【精彩点拨】 不妨设a≥b≥c>0,设法构造数组,利用排序不等式求解.
【自主解答】 不妨设a≥b≥c,
则A≥B≥C.
由排序不等式,得
aA+bB+cC=aA+bB+cC,
aA+bB+cC≥bA+cB+aC,
aA+bB+cC≥cA+aB+bC,
将以上三式相加,得
3(aA+bB+cC)≥(a+b+c)·(A+B+C)=π(a+b+c),
当且仅当A=B=C=时,等号成立.
∴≥,
即的最小值为.
规律总结:
1.分析待求函数的结构特征,构造两个有序数组.
2.运用排序原理求最值时,一定要验证等号是否成立,若等号不成立,则取不到最值.
[再练一题]
3.已知x,y,z是正数,且x+y+z=1,求t=++的最小值.
【解】 不妨设x≥y≥z>0,则x2≥y2≥z2,≥≥.
由排序不等式,乱序和≥反序和.
++
≥x2·+y2·+z2·
=x+y+z.
又x+y+z=1,++≥1,
当且仅当x=y=z=时,等号成立.
故t=++的最小值为1.
题型四、利用排序不等式求解简单的实际问题
例4 若某网吧的3台电脑同时出现了故障,对其维修分别需要45 min,25 min和30 min,每台电脑耽误1 min,网吧就会损失0.05元.在只能逐台维修的条件下,按怎样的顺序维修,才能使经济损失降到最小?
【精彩点拨】 这是一个实际问题,需要转化为数学问题.要使经济损失降到最小,即三台电脑维修的时间与等候的总时间之和最小,又知道若维修第一台用时间t1 min时,三台电脑等候维修的总时间为3t1 min,依此类推,等候的总时间为3t1+2t2+t3 min,求其最小值即可.
【自主解答】 设t1,t2,t3为25,30,45的任一排列,
由排序原理知3t1+2t2+t3≥3×25+2×30+45=180(min),
所以按照维修时间由小到大的顺序维修,可使经济损失降到最小.
规律总结:
1.首先理解题意,实际问题数学化,建立恰当模型.
2.三台电脑的维修时间3t1+2t2+t3就是问题的数学模型,从而转化为求最小值(运用排序原理).
[再练一题]
4.有5个人各拿一只水桶到水龙头接水,如果水龙头注满这5个人的水桶需要时间分别是4 min,8 min,6 min,10 min,5 min,那么如何安排这5个人接水的顺序,才能使他们等待的总时间最少?
【解】 根据排序不等式的反序和最小,可得最少时间为4×5+5×4+6×3+8×2+10×1=84(min).
即按注满时间为4 min,5 min,6 min,8 min,10 min依次等水,等待的总时间最少.
(四)归纳小结
排序不等式—
(五)随堂检测
1.已知x≥y,M=x4+y4,N=x3y+y3x,则M与N的大小关系是( )
A.M>N B.M≥N C.M<N D.M≤N
【解析】 由排序不等式,知M≥N.
【答案】 B
2.设a,b,c为正数,P=a3+b3+c3,Q=a2b+b2c+c2a,则P与Q的大小关系是( )
A.P>Q B.P≥Q C.P<Q D.P≤Q
【答案】 B
3.已知两组数1,2,3和4,5,6,若c1,c2,c3是4,5,6的一个排列,则c1+2c2+3c3的最大值是________,最小值是________.
【解析】 由排序不等式,顺序和最大,反序和最小,
∴最大值为1×4+2×5+3×6=32,最小值为1×6+2×5+3×4=28.
【答案】 32 28
六、板书设计
3.3排序不等式 | ||
教材整理1 顺序和、乱序和、反序和的概念
教材整理2 排序不等式 | 例1: 例2: 例3: 例4: |
学生板演练习 |
七、作业布置
八、教学反思
选修2-3第三章 统计案例3.2独立性检验的基本思想及其初步教案设计: 这是一份选修2-3第三章 统计案例3.2独立性检验的基本思想及其初步教案设计,共4页。教案主要包含了复习引入等内容,欢迎下载使用。
高中数学人教版新课标B必修1第三章 基本初等函数(Ⅰ)3.3 幂函数教学设计: 这是一份高中数学人教版新课标B必修1第三章 基本初等函数(Ⅰ)3.3 幂函数教学设计,共2页。
高中数学人教B版 (2019)选择性必修 第三册5.5 数学归纳法教学设计及反思: 这是一份高中数学人教B版 (2019)选择性必修 第三册5.5 数学归纳法教学设计及反思,共7页。教案主要包含了课时安排,教学重点,教学难点,教学过程,用数学归纳法证明等式,板书设计,作业布置,教学反思等内容,欢迎下载使用。