高中苏教版2.2椭圆教学设计

这是一份高中苏教版2.2椭圆教学设计，共18页。
1．椭圆的定义
平面内到两定点F1，F2的距离的和等于常数(大于F1F2)的点的轨迹叫做椭圆．两定点F1，F2叫做椭圆的焦点．
集合P＝{M|MF1＋MF2＝2a}，F1F2＝2c，其中a＞0，c＞0，且a，c为常数．
(1)当2a＞F1F2时，P点的轨迹是椭圆；
(2)当2a＝F1F2时，P点的轨迹是线段；
(3)当2a＜F1F2时，P点不存在．
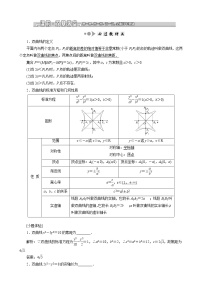
2．椭圆的标准方程和几何性质
[小题体验]
1．已知椭圆eq \f(x2,9)＋eq \f(y2,4)＝1的两焦点为F1，F2，过F1作直线交椭圆于A，B两点，则△ABF2的周长为________．
答案：12
2．已知直线x－2y＋2＝0过椭圆eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)的左焦点和一个顶点，则椭圆的方程为________．
解析：直线x－2y＋2＝0与x轴的交点为(－2,0)，即为椭圆的左焦点，故c＝2.
直线x－2y＋2＝0与y轴的交点为(0,1)，即为椭圆的顶点，故b＝1，所以a2＝b2＋c2＝5，故椭圆的方程为eq \f(x2,5)＋y2＝1.
答案：eq \f(x2,5)＋y2＝1
3．已知椭圆的一个焦点为F(1,0)，离心率为eq \f(1,2)，则椭圆的标准方程为________．
解析：设椭圆的标准方程为eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)．
因为椭圆的一个焦点为F(1,0)，离心率e＝eq \f(1,2)，
所以eq \b\lc\{\rc\ (\a\vs4\al\c1(c＝1，,\f(c,a)＝\f(1,2)，,a2＝b2＋c2，))解得eq \b\lc\{\rc\ (\a\vs4\al\c1(a＝2c＝2，,b2＝3，))
故椭圆的标准方程为eq \f(x2,4)＋eq \f(y2,3)＝1.
答案：eq \f(x2,4)＋eq \f(y2,3)＝1
1．求椭圆的标准方程时易忽视判断焦点的位置，而直接设方程为eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)．
2．注意椭圆的范围，在设椭圆eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)上点的坐标为P(x，y)时，|x|≤a，|y|≤b，这往往在求与点P有关的最值问题中特别有用，也是容易被忽略而导致求最值错误的原因．
[小题纠偏]
1．(2019·无锡一中月考)已知椭圆eq \f(x2,13－m)＋eq \f(y2,m－2)＝1的焦距为6，则m＝________.
解析：∵椭圆eq \f(x2,13－m)＋eq \f(y2,m－2)＝1的焦距为6，
∴当焦点在x轴时，(13－m)－(m－2)＝9，解得m＝3；
当焦点在y轴时，(m－2)－(13－m)＝9，解得m＝12.
答案：3或12
2．若方程eq \f(x2,5－k)＋eq \f(y2,k－3)＝1表示椭圆，则k的取值范围是________．
解析：由已知得eq \b\lc\{\rc\ (\a\vs4\al\c1(5－k＞0，,k－3＞0，,5－k≠k－3.))解得3＜k＜5且k≠4.
答案：(3,4)∪(4,5)
eq \a\vs4\al(考点一 椭圆的标准方程) eq \a\vs4\al(基础送分型考点——自主练透)
[题组练透]
1．与椭圆eq \f(x2,9)＋eq \f(y2,4)＝1有相同的焦点，且离心率为eq \f(\r(5),5)的椭圆的标准方程为________．
解析：由椭圆eq \f(x2,9)＋eq \f(y2,4)＝1，得a2＝9，b2＝4，∴c2＝a2－b2＝5，∴该椭圆的焦点坐标为(±eq \r(5)，0)．设所求椭圆方程为eq \f(x2,a′2)＋eq \f(y2,b′2)＝1，a′＞b′＞0，则c′＝eq \r(5)，又eq \f(c′,a′)＝eq \f(\r(5),5)，解得a′＝5.∴b′2＝25－5＝20，∴所求椭圆的标准方程为eq \f(x2,25)＋eq \f(y2,20)＝1.
答案：eq \f(x2,25)＋eq \f(y2,20)＝1
2．(2018·海门中学测试)已知中心在坐标原点的椭圆C的右焦点为F(1,0)，点F关于直线y＝eq \f(1,2)x的对称点在椭圆C上，求椭圆C的标准方程．
解：设点F关于y＝eq \f(1,2)x的对称点为P(x0，y0)，
又F(1,0)，所以eq \b\lc\{\rc\ (\a\vs4\al\c1(\f(y0－0,x0－1)＝－2，,\f(y0,2)＝\f(1,2)×\f(x0＋1,2)，))解得eq \b\lc\{\rc\ (\a\vs4\al\c1(x0＝\f(3,5)，,y0＝\f(4,5).))
又点P在椭圆上，设椭圆C的方程为eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)，
所以eq \b\lc\{\rc\ (\a\vs4\al\c1(\f(9,25a2)＋\f(16,25b2)＝1，,c2＝a2－b2＝1，))解得eq \b\lc\{\rc\ (\a\vs4\al\c1(a2＝\f(9,5)，,b2＝\f(4,5)，))
则椭圆C的方程为eq \f(x2,\f(9,5))＋eq \f(y2,\f(4,5))＝1.
3．求分别满足下列条件的椭圆的标准方程：
(1)经过点P(－2eq \r(3)，0)，Q(0,2)两点；
(2)与椭圆eq \f(x2,4)＋eq \f(y2,3)＝1有相同的焦点且经过点(2，－eq \r(3))．
解：(1)由题意，P，Q分别是椭圆长轴和短轴上的端点，且椭圆的焦点在x轴上，
所以a＝2eq \r(3)，b＝2，所求椭圆的标准方程为eq \f(x2,12)＋eq \f(y2,4)＝1.
(2)设椭圆eq \f(x2,4)＋eq \f(y2,3)＝1的左、右焦点分别为F1，F2，
所以F1(－1,0)，F2(1,0)，
所以所求椭圆焦点在x轴上，
设方程为eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)．
由题意得eq \b\lc\{\rc\ (\a\vs4\al\c1(a2－b2＝1，,\f(4,a2)＋\f(3,b2)＝1，))
解得a2＝4＋2eq \r(3)，b2＝3＋2eq \r(3)或a2＝4－2eq \r(3)，b2＝3－2eq \r(3)(舍去)，
所以椭圆的标准方程为eq \f(x2,4＋2\r(3))＋eq \f(y2,3＋2\r(3))＝1.
[谨记通法]
求椭圆标准方程的 2种常用方法
eq \a\vs4\al(考点二 椭圆的定义及其应用) eq \a\vs4\al(重点保分型考点——师生共研)
[典例引领]
已知椭圆eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)的右焦点为F2(1,0)，点Heq \b\lc\(\rc\)(\a\vs4\al\c1(2，\f(2\r(10),3)))在椭圆上．
(1)求椭圆的方程；
(2)点M在圆x2＋y2＝b2上，且点M在第一象限，过点M作圆x2＋y2＝b2的切线交椭圆于P，Q两点，求证：△PF2Q的周长是定值．
解：(1)设椭圆的左焦点为F1.
根据已知，椭圆的左右焦点分别是F1(－1,0)，F2(1,0)，半焦距c＝1，
因为Heq \b\lc\(\rc\)(\a\vs4\al\c1(2，\f(2\r(10),3)))在椭圆上，
所以2a＝HF1＋HF2＝ eq \r(2＋12＋\b\lc\(\rc\)(\a\vs4\al\c1(\f(2\r(10),3)))2)＋ eq \r(2－12＋\b\lc\(\rc\)(\a\vs4\al\c1(\f(2\r(10),3)))2)＝6.
所以a＝3，b＝2eq \r(2)，故椭圆的方程是eq \f(x2,9)＋eq \f(y2,8)＝1.
(2)证明：设P(x1，y1)，Q(x2，y2)，则eq \f(x\\al(2,1),9)＋eq \f(y\\al(2,1),8)＝1，
所以PF2＝eq \r(x1－12＋y\\al(2,1))＝ eq \r(x1－12＋8\b\lc\(\rc\)(\a\vs4\al\c1(1－\f(x\\al(2,1),9))))＝ eq \r(\b\lc\(\rc\)(\a\vs4\al\c1(\f(x1,3)－3))2).
因为0＜x1＜3，所以PF2＝3－eq \f(1,3)x1.
在圆x2＋y2＝b2中，M是切点，
所以PM＝eq \r(OP2－OM2)＝eq \r(x\\al(2,1)＋y\\al(2,1)－8)＝ eq \r(x\\al(2,1)＋8\b\lc\(\rc\)(\a\vs4\al\c1(1－\f(x\\al(2,1),9)))－8)＝eq \f(1,3)x1.
所以PF2＋PM＝3－eq \f(1,3)x1＋eq \f(1,3)x1＝3.
同理，QF2＋QM＝3，
所以F2P＋F2Q＋PQ＝3＋3＝6.
因此△PF2Q的周长是定值6.
[由题悟法]
利用定义求方程、焦点三角形及最值的方法
[即时应用]
1．已知椭圆的两个焦点为F1(－eq \r(2)，0)，F2(eq \r(2)，0)，点P是椭圆上的点，且△PF1F2的周长是4＋2eq \r(2)，则椭圆的标准方程为________．
解析：∵椭圆的两个焦点为F1(－eq \r(2)，0)，F2eq \b\lc\(\rc\)(\a\vs4\al\c1(\r(2)，0))，
∴椭圆的焦距为F1F2＝2eq \r(2).
∵△PF1F2的周长是4＋2eq \r(2)，
∴PF1＋PF2＋F1F2＝4＋2eq \r(2)，
可得PF1＋PF2＝4.
根据椭圆的定义，可得2a＝PF1＋PF2＝4，∴a＝2，
又∵c＝eq \r(2)，∴b＝eq \r(a2－c2)＝eq \r(2)，可得a2＝4，b2＝2.
故椭圆的标准方程为eq \f(x2,4)＋eq \f(y2,2)＝1.
答案：eq \f(x2,4)＋eq \f(y2,2)＝1
2．已知F1，F2是椭圆C：eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)的两个焦点，P为椭圆C上的一点，且eq \(PF1,\s\up7(―→))⊥eq \(PF2,\s\up7(―→)).若△PF1F2的面积为9，则b＝________.
解析：由题意知PF1＋PF2＝2a，eq \(PF1,\s\up7(―→))⊥eq \(PF2,\s\up7(―→))，所以PFeq \\al(2,1)＋PFeq \\al(2,2)＝F1Feq \\al(2,2)＝4c2，所以(PF1＋PF2)2－2PF1·PF2＝4c2，所以2PF1·PF2＝4a2－4c2＝4b2.所以PF1·PF2＝2b2，所以S△PF1F2＝ eq \f(1,2)PF1·PF2＝eq \f(1,2)×2b2＝b2＝9.所以b＝3.
答案：3
eq \a\vs4\al(考点三 椭圆的几何性质) eq \a\vs4\al(题点多变型考点——多角探明)
[锁定考向]
椭圆的几何性质是高考的热点，常见的命题角度有：
(1)求离心率的值或范围；
(2)根据椭圆的性质求参数的值或范围；
(3)焦点三角形的研究．
[题点全练]
角度一：求离心率的值或范围
1．(2019·连云港调研)已知椭圆eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)的左、右焦点分别为F1，F2，过F2且垂直于x轴的直线与椭圆交于A，B两点，O为坐标原点，若F1A⊥OB，则椭圆的离心率为________．
解析：由题意，可得Aeq \b\lc\(\rc\)(\a\vs4\al\c1(c，\f(b2,a)))，Beq \b\lc\(\rc\)(\a\vs4\al\c1(c，－\f(b2,a))).
∵F1A⊥OB，∴eq \f(\f(b2,a),2c)·eq \f(－\f(b2,a),c)＝－1，可得a2－c2＝eq \r(2)ac，
即e2＋eq \r(2)e－1＝0，解得e＝eq \f(\r(6)－\r(2),2)(负值舍去)．
答案：eq \f(\r(6)－\r(2),2)
2．从椭圆eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)上一点P向x轴作垂线，垂足恰为左焦点F1，A是椭圆与x轴正半轴的交点，B是椭圆与y轴正半轴的交点，且AB∥OP(O是坐标原点)，则该椭圆的离心率是________．
解析：由题意可设P(－c，y0)(c为半焦距)，kOP＝－eq \f(y0,c)，kAB＝－eq \f(b,a)，由于OP∥AB，所以－eq \f(y0,c)＝－eq \f(b,a)，y0＝eq \f(bc,a)，把Peq \b\lc\(\rc\)(\a\vs4\al\c1(－c，\f(bc,a)))代入椭圆方程得eq \f(－c2,a2)＋eq \f(\b\lc\(\rc\)(\a\vs4\al\c1(\f(bc,a)))2,b2)＝1，即eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(c,a)))2＝eq \f(1,2)，所以e＝eq \f(c,a)＝eq \f(\r(2),2).
答案：eq \f(\r(2),2)
角度二：根据椭圆的性质求参数的值或范围
3．若方程eq \f(x2,a－5)＋eq \f(y2,2)＝1表示的曲线为焦点在x轴上的椭圆，则实数a的取值范围是________．
解析：∵方程eq \f(x2,a－5)＋eq \f(y2,2)＝1表示的曲线为焦点在x轴上的椭圆，∴eq \b\lc\{\rc\ (\a\vs4\al\c1(a－5＞0，,a－5＞2，))解得a＞7.
∴实数a的取值范围是(7，＋∞)．
答案：(7，＋∞)
4．如果x2＋ky2＝2表示焦点在y轴上的椭圆，那么实数k的取值范围是________．
解析：x2＋ky2＝2转化为椭圆的标准方程，得eq \f(x2,2)＋eq \f(y2,\f(2,k))＝1，
因为x2＋ky2＝2表示焦点在y轴上的椭圆，
所以eq \f(2,k)＞2，解得0＜k＜1.所以实数k的取值范围是(0,1)．
答案：(0,1)
角度三：焦点三角形的研究
5．已知椭圆C：eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)的左、右焦点分别为F1，F2，点P为椭圆C上一点，且∠F1PF2＝60°.
(1)求椭圆C的离心率的范围；
(2)求证：△F1PF2的面积只与椭圆C的短半轴长有关．
解：(1)设PF1＝m，PF2＝n，则m＋n＝2a.
在△PF1F2中，由余弦定理可知，
4c2＝m2＋n2－2mncs 60°＝(m＋n)2－3mn
＝4a2－3mn≥4a2－3·eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(m＋n,2)))2＝4a2－3a2＝a2(当且仅当m＝n时取等号)．
所以eq \f(c2,a2)≥eq \f(1,4)，即e≥eq \f(1,2).
又0＜e＜1，所以e的取值范围是eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(1,2)，1)).
(2)证明：由(1)知mn＝eq \f(4,3)b2，
所以S△PF1F2＝eq \f(1,2)mnsin 60°＝eq \f(\r(3),3)b2，
即△PF1F2的面积只与短半轴长有关．
[通法在握]
1．应用椭圆几何性质的2个技巧
(1)与椭圆几何性质有关的问题要结合图形进行分析，即使画不出图形，思考时也要联想到一个图形．
(2)椭圆的范围或最值问题常常涉及一些不等式．例如－a≤x≤a，－b≤y≤b,0＜e＜1，在求椭圆的相关量的范围时，要注意应用这些不等关系．
2．求椭圆离心率的方法
(1)直接求出a，c的值，利用离心率公式直接求解．
(2)列出含有a，b，c的齐次方程(或不等式)，借助于b2＝a2－c2消去b，转化为含有e的方程(或不等式)求解．
[演练冲关]
1．已知椭圆eq \f(x2,9)＋eq \f(y2,4－k)＝1的离心率为eq \f(4,5)，则k的值为______．
解析：当9＞4－k＞0，即－5＜k＜4时，
a＝3，c2＝9－(4－k)＝5＋k，
所以eq \f(\r(5＋k),3)＝eq \f(4,5)，解得k＝eq \f(19,25).
当9＜4－k，即k＜－5时，a＝eq \r(4－k)，c2＝－k－5，
所以eq \f(\r(－k－5),\r(4－k))＝eq \f(4,5)，解得k＝－21，所以k的值为eq \f(19,25)或－21.
答案：eq \f(19,25)或－21
2．过椭圆eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)的左焦点F1作x轴的垂线交椭圆于点P，F2为椭圆的右焦点，若∠F1PF2＝60°，则椭圆的离心率为________．
解析：由题意，可设Peq \b\lc\(\rc\)(\a\vs4\al\c1(－c，\f(b2,a))).
因为在Rt△PF1F2中，PF1＝eq \f(b2,a)，F1F2＝2c，
∠F1PF2＝60°，所以eq \f(2ac,b2)＝eq \r(3).又因为b2＝a2－c2，
所以eq \r(3)c2＋2ac－eq \r(3)a2＝0，即eq \r(3)e2＋2e－eq \r(3)＝0，
解得e＝eq \f(\r(3),3)或e＝－eq \r(3)，
又因为e∈(0,1)，所以e＝eq \f(\r(3),3).
答案：eq \f(\r(3),3)
3．(2019·南京一模)设椭圆C：eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)的左、右焦点分别为F1，F2，P是椭圆C上的点，PF2⊥F1F2，∠PF1F2＝θ，若cs θ＝eq \f(1,3)，则椭圆C的离心率为________．
解析：∵PF2⊥F1F2，cs∠PF1F2＝eq \f(1,3)，F1F2＝2c，
∴PF1＝6c，PF2＝4eq \r(2)c，
又PF1＋PF2＝2a，∴6c＋4eq \r(2)c＝2a，
∴椭圆C的离心率e＝eq \f(2c,2a)＝eq \f(1,3＋2\r(2))＝3－2eq \r(2).
答案：3－2eq \r(2)
eq \a\vs4\al(考点四 直线与椭圆的位置关系) eq \a\vs4\al(重点保分型考点——师生共研)
[典例引领]
如图，在平面直角坐标系xOy中，椭圆C：eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)的离心率为eq \f(\r(3),2)，且过点eq \b\lc\(\rc\)(\a\vs4\al\c1(1，\f(\r(3),2))).过椭圆C的左顶点A作直线交椭圆C于另一点P，交直线l：x＝m(m＞a)于点M.已知点B(1,0)，直线PB交l于点N.
(1)求椭圆C的方程；
(2)若MB是线段PN的垂直平分线，求实数m的值．
解：(1)因为椭圆C的离心率为eq \f(\r(3),2)，所以a2＝4b2.
又因为椭圆C过点eq \b\lc\(\rc\)(\a\vs4\al\c1(1，\f(\r(3),2)))，所以eq \f(1,a2)＋eq \f(\f(3,4),b2)＝1，
解得a2＝4，b2＝1.
所以椭圆C的方程为eq \f(x2,4)＋y2＝1.
(2)设P(x0，y0)，且－2＜x0＜2, x0≠1，则eq \f(x\\al(2,0),4)＋yeq \\al(2,0)＝1.
因为MB是PN的垂直平分线，
所以点P关于点B的对称点N(2－x0，－y0)，
所以x0＝2－m.
由A(－2,0)，P(x0，y0)，
可得直线AP的方程为y＝eq \f(y0,x0＋2)(x＋2)，
令x＝m，得y＝eq \f(y0m＋2,x0＋2)，即Meq \b\lc\(\rc\)(\a\vs4\al\c1(m，\f(y0m＋2,x0＋2))).
因为PB⊥MB，所以kPB·kMB＝－1，
所以kPB·kMB＝eq \f(y0,x0－1)·eq \f(\f(y0m＋2,x0＋2),m－1)＝－1，
即eq \f(y\\al(2,0)m＋2,x0－1x0＋2m－1)＝－1.
因为eq \f(x\\al(2,0),4)＋yeq \\al(2,0)＝1.所以eq \f(x0－2m＋2,4x0－1m－1)＝1.
因为x0＝2－m ，所以化简得3m2－10m＋4＝0，
解得m＝eq \f(5±\r(13),3).
因为m＞2，所以m＝eq \f(5＋\r(13),3).
[由题悟法]
直线与椭圆的位置关系的解题策略
解决直线与椭圆的位置关系的相关问题，其常规思路是先把直线方程与椭圆方程联立，消元、化简，然后应用根与系数的关系建立方程，解决相关问题．
[即时应用]
(2018·南通、扬州调研)如图，在平面直角坐标系xOy中，已知椭圆eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)的离心率为eq \f(\r(2),2).A为椭圆上异于顶点的一点，点P满足eq \(OP,\s\up7(―→))＝2eq \(AO,\s\up7(―→)).
(1)若点P的坐标为(2，eq \r(2))，求椭圆的方程；
(2)设过点P的一条直线交椭圆于B，C两点，且eq \(BP,\s\up7(―→))＝meq \(BC,\s\up7(―→))，直线OA，OB的斜率之积为－eq \f(1,2)，求实数m的值．
解：(1) 因为eq \(OP,\s\up7(―→))＝2eq \(AO,\s\up7(―→))，而P(2，eq \r(2))，所以Aeq \b\lc\(\rc\)(\a\vs4\al\c1(－1，－\f(\r(2),2)))，
代入椭圆方程，得eq \f(1,a2)＋eq \f(2,4b2)＝1，①
又椭圆的离心率为eq \f(\r(2),2)，所以 eq \r(1－\f(b2,a2))＝eq \f(\r(2),2).②
由①②，得a2＝2，b2＝1.故椭圆的方程为eq \f(x2,2)＋y2＝1.
(2)设A(x1，y1)，B(x2，y2)，C(x3，y3)．
因为eq \(OP,\s\up7(―→))＝2eq \(AO,\s\up7(―→))，所以P(－2x1，－2y1)，
因为eq \(BP,\s\up7(―→))＝meq \(BC,\s\up7(―→))，所以(－2x1－x2，－2y1－y2)＝m(x3－x2，y3－y2)，
即eq \b\lc\{\rc\ (\a\vs4\al\c1(－2x1－x2＝mx3－x2，,－2y1－y2＝my3－y2，))于是eq \b\lc\{\rc\ (\a\vs4\al\c1(x3＝\f(m－1,m)x2－\f(2,m)x1，,y3＝\f(m－1,m)y2－\f(2,m)y1.))
代入椭圆方程，得eq \f(\b\lc\(\rc\)(\a\vs4\al\c1(\f(m－1,m)x2－\f(2,m)x1))2,a2)＋eq \f(\b\lc\(\rc\)(\a\vs4\al\c1(\f(m－1,m)y2－\f(2,m)y1))2,b2)＝1，
即eq \f(4,m2)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x\\al(2,1),a2)＋\f(y\\al(2,1),b2)))＋eq \f(m－12,m2)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x\\al(2,2),a2)＋\f(y\\al(2,2),b2)))－eq \f(4m－1,m2)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x1x2,a2)＋\f(y1y2,b2)))＝1，③
因为A，B在椭圆上，所以eq \f(x\\al(2,1),a2)＋eq \f(y\\al(2,1),b2)＝1，eq \f(x\\al(2,2),a2)＋eq \f(y\\al(2,2),b2)＝1. ④
因为直线OA，OB的斜率之积为－eq \f(1,2)，即eq \f(y1,x1)·eq \f(y2,x2)＝－eq \f(1,2)，
结合②知eq \f(x1x2,a2)＋eq \f(y1y2,b2)＝0. ⑤
将④⑤代入③，得eq \f(4,m2)＋eq \f(m－12,m2)＝1，
解得m＝eq \f(5,2).
一抓基础，多练小题做到眼疾手快
1．已知椭圆的中心在原点，焦点F1，F2在x轴上，P(2，eq \r(3))是椭圆上一点，且PF1，F1F2，PF2成等差数列，则椭圆的方程为______________．
解析：∵椭圆的中心在原点，焦点F1，F2在x轴上，
∴设椭圆方程为eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)，
∵P(2，eq \r(3))是椭圆上一点，且PF1，F1F2，PF2成等差数列，
∴eq \b\lc\{\rc\ (\a\vs4\al\c1(\f(4,a2)＋\f(3,b2)＝1，,2a＝4c，))且a2＝b2＋c2，解得a＝2eq \r(2)，b＝eq \r(6)，
∴椭圆的方程为eq \f(x2,8)＋eq \f(y2,6)＝1.
答案：eq \f(x2,8)＋eq \f(y2,6)＝1
2．已知椭圆的中心在坐标原点，焦点在x轴上，且长轴长为12，离心率为eq \f(1,2)，则该椭圆方程为________________．
解析：设椭圆的方程为eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)，因为2a＝12，eq \f(c,a)＝eq \f(1,2)，
所以a＝6，c＝3，b2＝27.所以椭圆的方程为eq \f(x2,36)＋eq \f(y2,27)＝1.
答案：eq \f(x2,36)＋eq \f(y2,27)＝1
3．椭圆eq \f(x2,2)＋y2＝1的左、右两焦点分别为F1，F2，椭圆上一点P满足∠F1PF2＝60°，则△F1PF2的面积为________．
解析：由题意，椭圆eq \f(x2,2)＋y2＝1的左、右两焦点分别为F1，F2，
则PF1＋PF2＝2eq \r(2)，F1F2＝2.
由余弦定理，得F1Feq \\al(2,2)＝PFeq \\al(2,1)＋PFeq \\al(2,2)－2PF1·PF2·cs 60°＝(PF1＋PF2)2－3PF1·PF2，
解得PF1·PF2＝eq \f(4,3).
故△F1PF2的面积S＝eq \f(1,2)PF1·PF2·sin 60°＝eq \f(\r(3),3).
答案：eq \f(\r(3),3)
4．(2019·南京名校联考)若n是2和8的等比中项，则圆锥曲线x2＋eq \f(y2,n)＝1的离心率是________．
解析：由n2＝2×8，得n＝±4，当n＝4时，曲线为椭圆，其离心率为e＝eq \f(\r(4－1),2)＝eq \f(\r(3),2)；当n＝－4时，曲线为双曲线，其离心率为e＝eq \f(\r(4＋1),1)＝eq \r(5).
答案：eq \f(\r(3),2)或eq \r(5)
5．(2018·北京东城模拟)已知椭圆C的中心在原点，一个焦点F(－2,0)，且长轴长与短轴长的比是2∶eq \r(3)，则椭圆C的方程是__________．
解析：设椭圆C的方程为eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)．
由题意知eq \b\lc\{\rc\ (\a\vs4\al\c1(a2＝b2＋c2，,a∶b＝2∶\r(3)，,c＝2，))解得a2＝16，b2＝12.
所以椭圆C的方程为eq \f(x2,16)＋eq \f(y2,12)＝1.
答案：eq \f(x2,16)＋eq \f(y2,12)＝1
6．(2018·启东中学检测)分别过椭圆C：eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)的左右焦点F1，F2所作的两条互相垂直的直线l1，l2的交点在椭圆上，则此椭圆的离心率的取值范围是________．
解析：设两直线交点为M，令MF1＝m，MF2＝n.由椭圆的定义可得m＋n＝2a，因为MF1⊥MF2，所以m2＋n2＝4c2，因为(m＋n)2＝m2＋n2＋2mn≤2(n2＋m2)，当且仅当m＝n＝a时取等号，即4a2≤2(4c2)，所以a≤eq \r(2)c，所以eq \f(c,a)≥eq \f(\r(2),2)，即e≥eq \f(\r(2),2)，因为e＜1，所以eq \f(\r(2),2)≤e＜1.
答案：eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(\r(2),2)，1))
二保高考，全练题型做到高考达标
1．(2019·启东模拟)设点P在圆x2＋(y－2)2＝1上移动，点Q在椭圆eq \f(x2,9)＋y2＝1上移动，则PQ的最大值是________．
解析：已知圆心C(0,2)，PQ≤PC＋CQ＝1＋CQ，故只需求CQ的最大值即可．
设Q(x，y)，
则 CQ＝eq \r(x2＋y－22)＝eq \r(91－y2＋y－22)＝eq \r(－8y2－4y＋13)＝ eq \r(－8\b\lc\(\rc\)(\a\vs4\al\c1(y＋\f(1,4)))2＋\f(27,2)).
∵ －1≤y≤1，∴ 当y＝－eq \f(1,4)时，CQmax＝eq \r(\f(27,2))＝eq \f(3\r(6),2)，
∴ PQmax＝1＋eq \f(3\r(6),2).
答案：1＋eq \f(3\r(6),2)
2．(2019·常州模拟)若椭圆C的长轴长是短轴长的3倍，则C的离心率为________．
解析：不妨设椭圆C的方程为eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)，则2a＝2b×3，即a＝3b.
所以a2＝9b2＝9(a2－c2)．
即eq \f(c2,a2)＝eq \f(8,9)，
所以e＝eq \f(c,a)＝eq \f(2\r(2),3).
答案：eq \f(2\r(2),3)
3．(2018·镇江期末)已知椭圆eq \f(x2,m)＋eq \f(y2,n)＝1(m＞n＞0)的左、右焦点分别为F1，F2，P是以椭圆短轴为直径的圆上任意一点，则eq \(PF1,\s\up7(―→))·eq \(PF2,\s\up7(―→))＝________.
解析：法一：eq \(PF1,\s\up7(―→))·eq \(PF2,\s\up7(―→))＝(eq \(PO,\s\up7(―→))＋eq \(OF1,\s\up7(―→)))·(eq \(PO,\s\up7(―→))＋eq \(OF2,\s\up7(―→)))＝(eq \(PO,\s\up7(―→))＋eq \(OF1,\s\up7(―→)))·(eq \(PO,\s\up7(―→))－eq \(OF1,\s\up7(―→)))＝|eq \(PO,\s\up7(―→))|2－|eq \(OF1,\s\up7(―→))|2＝n－(m－n)＝2n－m.
法二：设F1(－c,0)，F2(c,0)，P(x，y)，则x2＋y2＝n，eq \(PF1,\s\up7(―→))·eq \(PF2,\s\up7(―→))＝(x＋c)(x－c)＋y2＝x2＋y2－c2＝n－(m－n)＝2n－m.
答案：2n－m
4．(2018·苏北四市一模)如图，在平面直角坐标系xOy中，已知点A，B1，B2分别为椭圆C：eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)的右、下、上顶点，F是椭圆C的右焦点．若B2F⊥AB1，则椭圆C的离心率是________．
解析：因为F(c,0)，B2(0，b)，B1(0，－b)，A(a,0)，所以eq \(B2F,\s\up7(―→))＝(c，－b)，eq \(B1A,\s\up7(―→))＝(a，b)．因为B2F⊥AB1，所以ac－b2＝0，即c2＋ac－a2＝0，故e2＋e－1＝0，解得e＝eq \f(－1＋\r(5),2)(负值舍去)．
答案：eq \f(\r(5)－1,2)
5．如图，已知椭圆C的中心为原点O，F(－2eq \r(5)，0)为C的左焦点，P为C上一点，满足OP＝OF，且PF＝4，则椭圆C的方程为________．
解析：设椭圆的标准方程为eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)，焦距为2c，右焦点为F′，连结PF′，如图所示．因为F(－2eq \r(5)，0)为C的左焦点，所以c＝2eq \r(5).由OP＝OF＝OF′知，∠FPF′＝90°，即FP⊥PF′.在Rt△PFF′中，由勾股定理，得PF′＝eq \r(FF′2－PF2)＝eq \r(4\r(5)2－42)＝8.由椭圆定义，得PF＋PF′＝2a＝4＋8＝12，所以a＝6，a2＝36，于是b2＝a2－c2＝36－(2eq \r(5))2＝16，所以椭圆C的方程为eq \f(x2,36)＋eq \f(y2,16)＝1.
答案：eq \f(x2,36)＋eq \f(y2,16)＝1
6.(2019·启东月考)如图所示，A，B是椭圆的两个顶点，C是AB的中点，F为椭圆的右焦点，OC的延长线交椭圆于点M，且OF＝eq \r(2)，若MF⊥OA，则椭圆的方程为________．
解析：∵F为椭圆的右焦点，OF＝eq \r(2)，∴c＝eq \r(2).
设椭圆方程为eq \f(x2,b2＋2)＋eq \f(y2,b2)＝1(b＞0)，
∵A，B是椭圆的两个顶点，∴Aeq \b\lc\(\rc\)(\a\vs4\al\c1(\r(b2＋2)，0))，B(0，b)．
又∵C是AB的中点，∴Ceq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(b2＋2),2)，\f(b,2))).由OC的延长线交椭圆于点M，MF⊥OA，得Meq \b\lc\(\rc\)(\a\vs4\al\c1(\r(2)，\f(b2,\r(b2＋2)))).
∵kOM＝kOC，∴eq \f(\f(b2,\r(b2＋2)),\r(2))＝eq \f(\f(b,2),\f(\r(b2＋2),2))，∴b＝eq \r(2)，
故所求椭圆的方程为eq \f(x2,4)＋eq \f(y2,2)＝1.
答案：eq \f(x2,4)＋eq \f(y2,2)＝1
7．在平面直角坐标系xOy中，椭圆C的中心为原点，焦点F1，F2在x轴上，离心率为eq \f(\r(2),2).过F1的直线l交C于A，B两点，且△ABF2的周长为16，那么C的方程为________．
解析：设椭圆C的方程为eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)，
因为AB过F1且A，B在椭圆C上，
所以△ABF2的周长＝AB＋AF2＋BF2
＝AF1＋AF2＋BF1＋BF2
＝4a＝16，
所以a＝4.
又离心率e＝eq \f(c,a)＝eq \f(\r(2),2)，
所以c＝2eq \r(2)，
所以b2＝a2－c2＝8，
所以椭圆C的方程为eq \f(x2,16)＋eq \f(y2,8)＝1.
答案：eq \f(x2,16)＋eq \f(y2,8)＝1
8．(2019·句容月考)离心率e＝eq \f(1,3)，焦距为4的椭圆的标准方程为________________．
解析：∵椭圆的离心率e＝eq \f(1,3)，焦距为4，∴c＝2，a＝6，
∴b2＝32，∴椭圆的标准方程为eq \f(x2,36)＋eq \f(y2,32)＝1或eq \f(y2,36)＋eq \f(x2,32)＝1.
答案：eq \f(x2,36)＋eq \f(y2,32)＝1或eq \f(y2,36)＋eq \f(x2,32)＝1
9．已知椭圆eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)，F1，F2分别为椭圆的左、右焦点，A为椭圆的上顶点，直线AF2交椭圆于另一点B.
(1)若∠F1AB＝90°，求椭圆的离心率．
(2)若eq \(AF2,\s\up7(―→))＝2eq \(F2B,\s\up7(―→))，eq \(AF1,\s\up7(―→))·eq \(AB,\s\up7(―→))＝eq \f(3,2)，求椭圆的方程．
解：(1)若∠F1AB＝90°，则△AOF2为等腰直角三角形，所以有OA＝OF2，即b＝c.
所以a＝eq \r(2)c，e＝eq \f(c,a)＝eq \f(\r(2),2).
(2)由题知A(0，b)，F1(－c,0)，F2(c,0)，其中c＝eq \r(a2－b2)，设B(x，y)．
由eq \(AF2,\s\up7(―→))＝2eq \(F2B,\s\up7(―→))，得(c，－b)＝2(x－c，y)，
解得x＝eq \f(3c,2)，y＝－eq \f(b,2)，
即Beq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3c,2)，－\f(b,2))).
将B点坐标代入eq \f(x2,a2)＋eq \f(y2,b2)＝1，得eq \f(\f(9,4)c2,a2)＋eq \f(\f(b2,4),b2)＝1，
即eq \f(9c2,4a2)＋eq \f(1,4)＝1，解得a2＝3c2.①
又由eq \(AF1,\s\up7(―→))·eq \(AB,\s\up7(―→))＝(－c，－b)·eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3c,2)，－\f(3b,2)))＝eq \f(3,2)，
得b2－c2＝1，即有a2－2c2＝1.②
由①②解得c2＝1，a2＝3，从而有b2＝2.
所以椭圆的方程为eq \f(x2,3)＋eq \f(y2,2)＝1.
10．(2018·南京学情调研)如图，在平面直角坐标系xOy中，椭圆C：eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)的左、右焦点分别为F1，F2，P为椭圆上一点(在x轴上方)，连结PF1并延长交椭圆于另一点Q，设eq \(PF1,\s\up7(―→))＝λeq \(F1Q,\s\up7(―→)).
(1)若点P的坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(1，\f(3,2)))，且△PQF2的周长为8，求椭圆C的方程；
(2)若PF2⊥x轴，且椭圆C的离心率e∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(1,2)，\f(\r(2),2)))，求实数λ的取值范围．
解：(1)因为F1，F2为椭圆C的两焦点，且P，Q为椭圆上的点，
所以PF1＋PF2＝QF1＋QF2＝2a，
从而△PQF2的周长为4a，
由题意得4a＝8，解得a＝2.
因为点P的坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(1，\f(3,2)))，且在椭圆上，
所以eq \f(1,4)＋eq \f(9,4b2)＝1，解得b2＝3.
所以椭圆C的方程为eq \f(x2,4)＋eq \f(y2,3)＝1.
(2)因为PF2⊥x轴，且P在x轴上方，所以可设P(c，y0)，且y0＞0，Q(x1，y1)．
因为点P在椭圆上，所以eq \f(c2,a2)＋eq \f(y\\al(2,0),b2)＝1，
解得y0＝eq \f(b2,a)，即Peq \b\lc\(\rc\)(\a\vs4\al\c1(c，\f(b2,a))).
因为F1(－c,0)，
所以eq \(PF1,\s\up7(―→))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(－2c，－\f(b2,a)))，eq \(F1Q,\s\up7(―→))＝(x1＋c，y1)．
由eq \(PF1,\s\up7(―→))＝λeq \(F1Q,\s\up7(―→))，得－2c＝λ(x1＋c)，－eq \f(b2,a)＝λy1，
解得x1＝－eq \f(λ＋2,λ)c，y1＝－eq \f(b2,λa)，
所以Qeq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(λ＋2,λ)c，－\f(b2,λa))).
因为点Q在椭圆上，所以eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(λ＋2,λ)))2e2＋eq \f(b2,λ2a2)＝1，
即(λ＋2)2e2＋(1－e2)＝λ2，即(λ2＋4λ＋3)e2＝λ2－1.
因为λ＋1≠0，所以(λ＋3)e2＝λ－1，
从而λ＝eq \f(3e2＋1,1－e2)＝eq \f(4,1－e2)－3.
因为e∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(1,2)，\f(\r(2),2)))，所以eq \f(1,4)≤e2≤eq \f(1,2)，即eq \f(7,3)≤λ≤5.
所以λ的取值范围为eq \b\lc\[\rc\](\a\vs4\al\c1(\f(7,3)，5)).
三上台阶，自主选做志在冲刺名校
1．(2019·宿迁调研)已知椭圆C：eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)的左焦点为F，下顶点为A.若平行于AF且在y轴上截距为3－eq \r(2) 的直线与圆x2＋(y－3)2＝1相切，则该椭圆的离心率为________．
解析：由椭圆C：eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)的左焦点为F，下顶点为A，可得AF的斜率为－eq \f(b,c)，则平行于AF且在y轴上截距为3－eq \r(2)的直线方程为y＝－eq \f(b,c)x＋3－eq \r(2).由该直线与圆x2＋(y－3)2＝1相切，可得eq \f(|－3＋3－\r(2)|,\r(1＋\f(b2,c2)))＝1，解得b＝c，所以e＝eq \f(c,a)＝eq \f(1,\r(2))＝eq \f(\r(2),2).
答案：eq \f(\r(2),2)
2．(2018·连云港质检)已知两定点A(－2,0)和B(2,0)，动点P(x，y)在直线l：y＝x＋3上移动，椭圆C以A，B为焦点且经过点P，则椭圆C的离心率的最大值为________．
解析：设点A关于直线l的对称点为A1(x1，y1)，
则有eq \b\lc\{\rc\ (\a\vs4\al\c1(\f(y1,x1＋2)＝－1，,\f(y1,2)＝\f(x1－2,2)＋3，))解得x1＝－3，y1＝1，
易知PA＋PB的最小值等于A1B＝eq \r(26)，
因此椭圆C的离心率e＝eq \f(AB,PA＋PB)＝eq \f(4,PA＋PB)的最大值为eq \f(2\r(26),13).
答案：eq \f(2\r(26),13)
3.已知椭圆M：eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)的右焦点F的坐标为(1,0)，P，Q为椭圆上位于y轴右侧的两个动点，使PF⊥QF，C为PQ中点，线段PQ的垂直平分线交x轴，y轴于点A，B(线段PQ不垂直x轴)，当Q运动到椭圆的右顶点时，PF＝eq \f(\r(2),2).
(1)求椭圆M的方程；
(2)若S△ABO∶S△BCF＝3∶5，求直线PQ的方程．
解：(1)当Q运动到椭圆的右顶点时，PF⊥x轴，
所以PF＝eq \f(b2,a)＝eq \f(\r(2),2)，
又c＝1，a2＝b2＋c2，所以a＝eq \r(2)，b＝1.
所以椭圆M的方程为eq \f(x2,2)＋y2＝1.
(2)设直线PQ的方程为y＝kx＋b，显然k≠0，
联立椭圆方程得：(2k2＋1)x2＋4kbx＋2(b2－1)＝0，
设点P(x1，y1)，Q(x2，y2),
则eq \b\lc\{\rc\ (\a\vs4\al\c1(x1＋x2＝\f(－4kb,2k2＋1)＞0， ①,x1x2＝\f(2b2－1,2k2＋1)＞0， ②,Δ＝82k2－b2＋1＞0， ③))
由eq \(PF,\s\up7(―→))·eq \(QF,\s\up7(―→))＝0，得(x1－1)(x2－1)＋y1y2＝0，
即(k2＋1)x1x2＋(kb－1)(x1＋x2)＋b2＋1＝0，
代入化简得3b2－1＋4kb＝0.④
由y1＋y2＝k(x1＋x2)＋2b＝eq \f(2b,2k2＋1)，
得Ceq \b\lc\(\rc\)(\a\vs4\al\c1(\f(－2kb,2k2＋1)，\f(b,2k2＋1)))，
所以线段PQ的中垂线AB的方程为
y－eq \f(b,2k2＋1)＝－eq \f(1,k)eq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(2kb,2k2＋1))).
令y＝0，x＝0，可得Aeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(－kb,2k2＋1)，0))，Beq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(－b,2k2＋1)))，
则A为BC中点，
故eq \f(S△BCF,S△ABO)＝eq \f(2S△ABF,S△ABO)＝eq \f(2AF,AO)＝eq \f(21－xA,xA)＝2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,xA)－1)).
由④式得，k＝eq \f(1－3b2,4b)，则xA＝eq \f(－kb,2k2＋1)＝eq \f(6b4－2b2,9b4＋2b2＋1)，
所以eq \f(S△BCF,S△ABO)＝2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,xA)－1))＝eq \f(6b4＋8b2＋2,6b4－2b2)＝eq \f(5,3)，解得b2＝3.
所以b＝eq \r(3)，k＝－eq \f(2\r(3),3)或b＝－eq \r(3)，k＝eq \f(2\r(3),3).
经检验，满足条件①②③，
故直线PQ的方程为y＝eq \f(2\r(3),3)x－eq \r(3)或y＝－eq \f(2\r(3),3)x＋eq \r(3).
标准方程
eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)
eq \f(y2,a2)＋eq \f(x2,b2)＝1(a＞b＞0)
图形
性 质
范围
x∈[－a，a]，y∈[－b，b]
x∈[－b，b]，y∈[－a，a]
对称性
对称轴：坐标轴；对称中心：原点
顶点
A1(－a,0)，A2(a,0)
B1(0，－b)，B2(0，b)
A1(0，－a)，A2(0，a)
B1(－b,0)，B2(b,0)
离心率
e＝eq \f(c,a)，且e∈(0,1)
a，b，c的关系
c2＝a2－b2
定义法
根据椭圆的定义，确定a2，b2的值，结合焦点位置可写出椭圆方程
待定系数法
若焦点位置明确，则可设出椭圆的标准方程，结合已知条件求出a，b；若焦点位置不明确，则需要分焦点在x轴上和y轴上两种情况讨论，也可设椭圆的方程为Ax2＋By2＝1(A＞0，B＞0，A≠B)
求方程
通过对题设条件分析、转化后，能够明确动点P满足椭圆的定义，便可直接求解其轨迹方程
求焦点三角形
利用定义求焦点三角形的周长和面积．解决焦点三角形问题常利用椭圆的定义、正弦定理或余弦定理．其中PF1＋PF2＝2a两边平方是常用技巧
求最值
抓住PF1与PF2之和为定值，可联系到基本不等式求PF1·PF2的最值；利用定义PF1＋PF2＝2a转化或变形，借助三角形性质求最值