高中数学人教版新课标A必修11.2.2函数的表示法示范课ppt课件

这是一份高中数学人教版新课标A必修11.2.2函数的表示法示范课ppt课件，共36页。PPT课件主要包含了对应关系，任意一个，唯一确定，非空数集，分段函数及应用，映射的概念，分段函数的实际应用等内容，欢迎下载使用。

某魔术师猜牌的表演过程是这样的，表演者手中持有六张扑克牌，不含王牌和牌号数相同的牌，让6位观众每人从他手里任摸一张，并嘱咐摸牌时看清和记住自己的牌号，牌号数是这样规定的，A为1，J为11，Q为12，K为13，其余的以牌上的数字为准，然后，表演者让他们按如下的方法进行计算，将自己的牌号乘2加3后乘5，再减去25，把计算结果告诉表演者(要求数值绝对准确)，表演者便能立即准确地猜出谁拿的是什么牌，你能说出其中的道理吗？
1.分段函数所谓分段函数，是指在定义域的不同部分，有不同的__________的函数．[知识点拨]　分段函数是一个函数，不要把它误认为是几个函数．分段函数的定义域是各段定义域的并集，值域是各段值域的并集．
2．映射(1)定义：一般地，设A，B是两个非空的集合，如果按某一个确定的对应关系f，使对于集合A中的_________元素x，在集合B中都有__________的元素y与之对应，那么就称对应f：A→B为从集合____到集合____的一个映射．[知识点拨]　满足下列条件的对应f：A→B为映射：(1)A，B为非空集合；(2)有对应法则f；(3)集合A中的每一个元素在集合B中均有唯一元素与之对应．
(2)映射与函数的关系：函数是特殊的映射，即当两个集合A，B均为__________时，从A到B的映射就是函数，所以函数一定是映射，而映射不一定是函数，映射是函数的推广．[知识点拨]　函数新概念，记准三要素；定义域值域，关系式相连；函数表示法，记住也不难；图象和列表，解析最常见；函数变映射，只是数集变；不再是数集，任何集不限．
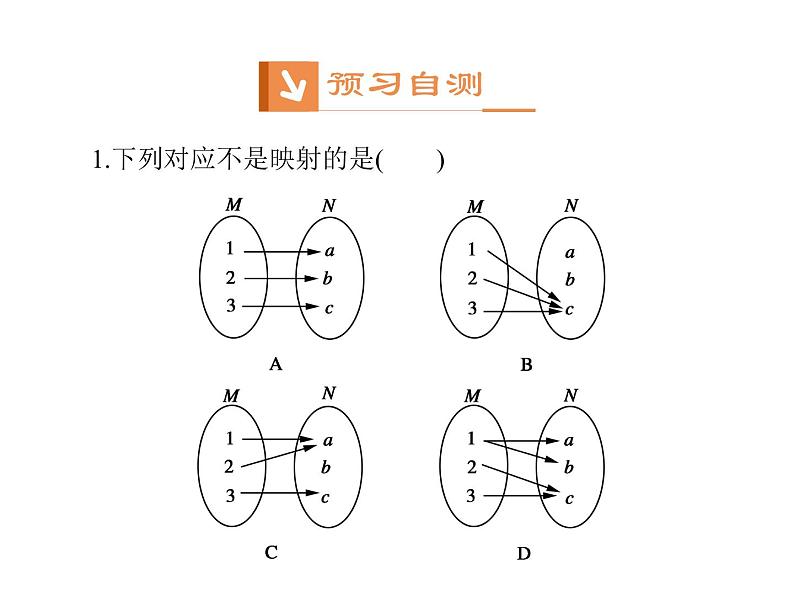
[答案]　D[解析]　结合映射的定义可知A，B，C均满足M中任意一个数x，在N中有唯一确定的y与之对应，而D中元素1在N中有a，b两个元素与之对应，故不是映射．
[答案]　D[解析]　根据分段函数定义域的确定原则：将每一段上函数的自变量的范围取并集，即：[－5,0]∪[2,6)．
[思路分析]　给出的函数是分段函数，应注意在不同的自变量取值范围内有不同的解析式．(1)根据自变量的值，选用相应关系式求函数值．(2)在不同的区间，依次画出函数图象．
[点评]　本题易出现对分段函数的定义域与值域的求法不清楚而致错．[规律总结]　1.解答本题第(1)、(2)题时，应注意自变量的取值范围．2．分段函数求值，一定要注意所给自变量的值所在的范围，代入相应的解析式求解．3．画图象时，则应分段分别作出其图象，在作每一段图象时，先不管定义域的限制，用虚线作出其图象，再用实线保留定义域内的一段图象即可．
[思路分析]　(1)从集合A到B的映射中元素是怎样对应的？(2)怎样判断一个对应是映射？[解析]　(1)A中元素3在对应关系f的作用下与3的差的绝对值为0，而0∉B，故不是映射．(2)因为一个圆有无数个内接矩形，即集合A中任何一个元素在集合B中有无数个元素与之对应，故不是映射．(3)对A中任何一个元素，按照对应关系f，在B中都有唯一的元素与之对应，符合映射定义，是映射．
[思路分析]　(1)点P位置不同△ABP的形状一样吗？(2)注意该函数的定义域．
(3)即f(x)≥2，当0≤x≤4时，2x≥2，∴x≥1，当8[错因分析]　以上解法的错误之处在于误解了映射的定义．a4＝10或a2＋3a＝10都有可能，因而要分类讨论．[思路分析]　对于A映射f：A→B，A中的元素x的象可能是B中的任意一个元素，故在解此类题时要将问题考虑全面．
A．①、②　　　B．①、④C．②、⑤D．①、②、③[答案]　D[解析]　由图知①②中元素a1在B中对应元素不唯一，③中元素a2在B中无象，都不是映射，④⑤是映射，故选D.
[答案]　5[解析]　f(2)＝2a－1＝3，∴a＝2，∴f(x)＝2x－1，∴f(3)＝5.