北师大版九年级下册4 二次函数的应用教学ppt课件

这是一份北师大版九年级下册4 二次函数的应用教学ppt课件，文件包含北师大版数学九年级下册第二章二次函数-4二次函数的应用第1课时课件pptx、北师大版数学九年级下册第二章二次函数-4二次函数的应用-第1课时利用二次函数解决面积问题和抛物线形问题教案doc等2份课件配套教学资源，其中PPT共15页， 欢迎下载使用。
4       二次函数的应用第1课时 利用二次函数解决面积问题和抛物线形问题【知识与技能】经历探究解决图形的最大面积问题与抛物线形问题的过程，进一步获得利用数学方法解决实际问题的经验.【过程与方法】经历探索问题的过程，获得利用数学方法解决实际问题的经验，感受数学模型和数学应用的价值，通过观察、比较、推理、交流等过程，获得一些研究问题与合作交流的方法与经验.【情感态度】通过动手实践及同学之间的合作与交流，让学生积累经验，发展学习动力.【教学重点】会根据不同的条件，利用二次函数解决生活中的实际问题 【教学难点】从几何背景及实际情景中抽象出函数模型.
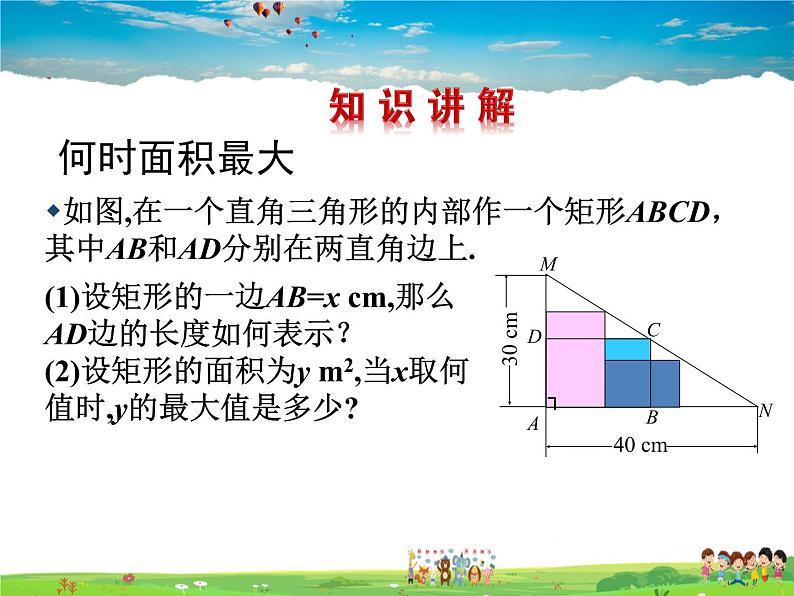
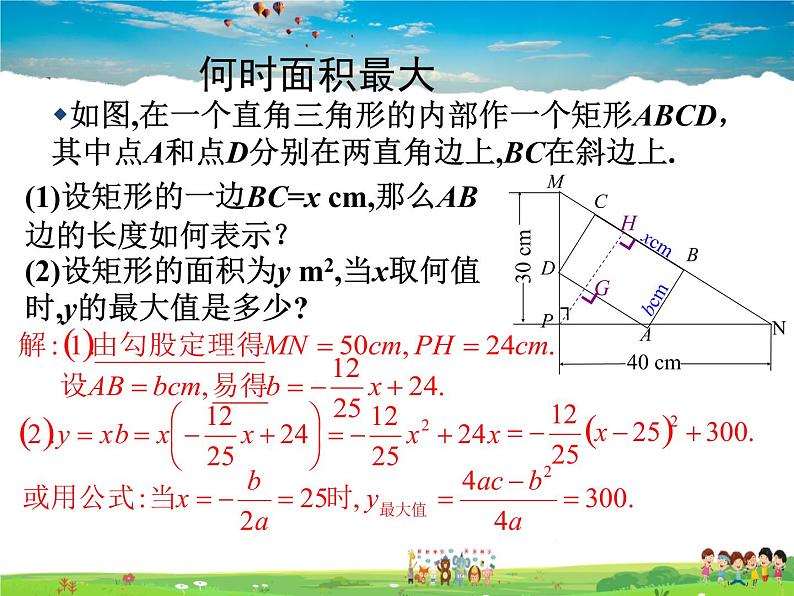
一、情景导入，初步认知问题1： 某开发商计划开发一块三角形土地，它的底边长100米，高80米.开发商要沿着底边修一座底面是矩形的大楼，这座大楼地基 的最大面积是多少？要解决类似问题1的实际问题，实际上也就是求面积最大的问题，在数学中也就是求最大值的问题.要解决问题2，实际上也就是建立二次函数模型解决抛物线形问题.这节课我们看能否用已学过的数学知识来 解决以上问题.【教学说明】通过几个实际情景设置悬念，引入新课.二、思考探究，获取新知1.求下列函数的最大值或最小值.（1）y=2x2-3x-5；（2）y=-x2-3x+4.分析：由于函数y=2x2-3x-5和y=-x2-3x+4的自变量x的取值范围是全体实数，所以只要确定它们的图象有最高点或最低点，就可以确定函数有最大值或最小值.解：（1)二次函数y=2x2-3x-5；中的二次项系数2＞0，因此抛物线y=2x2-3x-5有最低点，即函数有最小值.因为y=2x2-3x-5= 所以当时，函数y=2x2-3x-5有最小值是.（2）二次函数y=-x2-3x+4中的二次项系数-1＜0，因此抛物线y=-x2-3x+4有最高点，即函数有最大值.因为y=-x2-3x+4= ，所以当时，函数y=-x2-3x+4有最大值是【教学说明】由于学习这一部分所用的基本知识点是求二次函数的最值，因此首先和同学们一起复习二次函数最值的求法:对于一般式，要求掌握配方法的同时，也能利用基本结论;对于顶点式，要求能直接说出其最值及取得最值时自变量的值.2.杂技团进行杂技表演，演员从跷跷板一端弹跳到人梯顶端，其身体（看成一点）的路线（由A到B）是抛物线y=-x2+3x+1的一部分，如图.（1）求演员离地面的最大高度；（2）已知人梯高BC=3.4m，在一次表演中，人梯到起跳点A的水平距离是4m，则这次表演是否成功？请说明理由.  【教学说明】在前面学习的基础上，适当放手让学生独立思考、分析并总结此类问题的解题步骤，通过类比的思想，总结二次函数在实际问题中的应用.三、运用新知，深化理解1.见教材P46例12. 如图，在一个直角三角形的内部作一个矩形ABCD，其中AB和AD分别在两直角边上．如果设矩形的一边AB=x m，那么当x为多少时，矩形面积最大？最大面积是多少？3.一座拱桥的轮廓是抛物线形（如图1），拱高6m，跨度是20m，相邻两支柱间的距离为5m.   （1）将抛物线放在所给的直角坐标系中（如图2），其表达式是y=ax2+c的形式，请根据所给数据求出a，c的值   （2）求支柱MN的长度；（3）拱桥下地平面是双向行车道（正中间是一条宽2m的隔离带），其中的一条行车道能否并排行驶宽2m、高3m的三辆卡车（卡车间的间隔忽略不计）？请说明理由.解：（1）根据题目条件，A，B，C的坐标分别是（-10，0），（10，0），（0，6），将C，B的坐标代入y=ax2+c，得（2）由（1）可知，抛物线的表达式是y=-x2+6.可设N（5，yN），所以yN=-×52+6=4.5，所以支柱MN的长度是10-4.5=5.5（m）.（3）能，理由如下： 如图3，设DE是隔离带的宽，EG是三辆卡车的宽度和，则点G的坐标是（7，0）.过点G作GH垂直于AB交抛物线于点H，则yH=-×72+6>3.根据抛物线的特点可知，一条行车道能并排行驶宽2m，高3m的三辆卡车.【教学说明】展示教材上的例题，和同学一起从问题中抽象出二次函数的模型，并求其最值，同时对例题进行变式，训练学生的发散思维能力.四、师生互动、课堂小结引导学生总结，确定问题的解决方法：在一些涉及到变量的最大值或最小值的应用问题中，可以考虑利用二次函数最值方面的性质去 解决步骤：第一步:设自变量；第二步:建立函数的解析式；第三步：确定自变量的取值范围；第四步：根据顶点坐标公式或配方法求出最大值或最小值（在自变量的取值范围内）.1.布置作业：教材“习题2.8”中第2、3题.2.完成练习册中本课时的练习.在教学中一定要注意学生易错地方：学生往往列出表达式后不根据背景写出自变量的范围；求最值时，只知代入顶点坐标公式，不考虑自变量范围.