专题68 利用同构特点解决问题（解析版）学案

专题68  利用同构特点解决问题

【热点聚焦与扩展】

本专题在分析研究近几年高考题及各地模拟题的基础上，举例说明利用同构特点解决问题的方法与技巧.

1、同构式：是指除了变量不同，其余地方均相同的表达式

2、同构式的应用：

（1）在方程中的应用：如果方程和呈现同构特征，则可视为方程的两个根

（2）在不等式中的应用：如果不等式的两侧呈现同构特征，则可将相同的结构构造为一个函数，进而和函数的单调性找到联系.可比较大小或解不等式

（3）在解析几何中的应用：如果满足的方程为同构式，则为方程所表示曲线上的两点.特别的，若满足的方程是直线方程，则该方程即为直线的方程

（4）在数列中的应用：可将递推公式变形为“依序同构”的特征，即关于与的同构式，从而将同构式设为辅助数列便于求解

【经典例题】

例1．（2020·通榆县第一中学校高三三模）已知函数，若()，则的取值范围是（    ）

A． B． C． D．

【答案】C

【解析】函数的图象如下图所示：

因为，所以有

因为，所以，

因此有，，

，所以，所以，

所以，

故选：C

例2．（2020·北京四中高三三模）已知函数 给出下列三个结论：① 当时，函数的单调递减区间为；② 若函数无最小值，则的取值范围为；③ 若且，则，使得函数恰有3个零点,,，且. 其中，所有正确结论的个数是（    ）

A．0 B．1 C．2 D．3

【答案】C

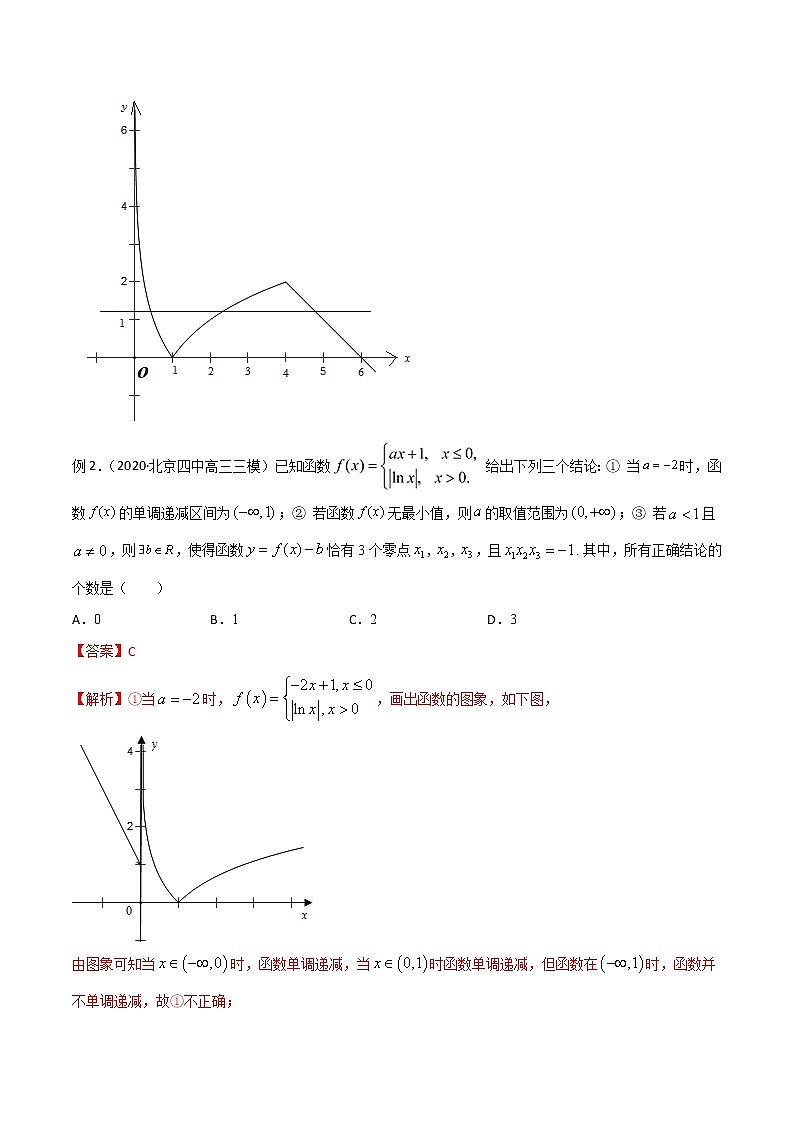
【解析】①当时，，画出函数的图象，如下图，

由图象可知当时，函数单调递减，当时函数单调递减，但函数在时，函数并不单调递减，故①不正确；

②当时，时，函数单调递增，并且当时，，所以函数没有最小值；

当时，，，函数的最小值是0；

当时，时，函数单调递减，函数的最小值是1，当时，，的最小值是0，综上可知函数的最小值是0，

综上，若函数没有最小值，只需满足，故②正确；

对于③，令，当时，，当时，，

不妨设，，，，

则，令，可得，

当时，，则三个零点，

当时，，则三个零点.

综上可知③正确；

故选：C

例3．（2020·天津南开中学高三三模）已知函数，若关于的方程有5个不同的实数根，则实数的取值范围是（    ）

A． B． C． D．

【答案】A

【解析】设，可得，

当时，，函数单调递增；

当时，，函数单调递减，

所以当时，函数取得极大值也是最大值，最大值为，

由方程可化为，

解得或，

画出函数的图象，如图所示，

要使得关于的方程有5个不同的实数根，

则满足，解得，

即实数的取值范围是.

故选：A

例4．（2020·蕉岭县蕉岭中学高三三模）已知奇函数的导函数为，当时，，若，则的大小关系正确的是（    ）

A． B． C． D．

【答案】C

【解析】令，则，所以单调递增，
因为，所以即，
又为奇函数，所以，

所以.

故选：C.

例5．（2020·山东新泰市第一中学高三三模）已知是可导的函数，且，对于恒成立，则下列不等关系正确的是（    ）

A．， B．，

C．， D．，

【答案】C

【解析】设，

则，

，

，即在上单调递减，

，即，

即，故选项A不正确；

，即，

即，故选项D不正确；

，

即，即．故选项B不正确；

故选：C．

例6．（2020·辽宁大连·高三三模）设数列的前项和为．若，，，则值为（    ）

A．363 B．121 C．80 D．40

【答案】B

【解析】因为，

所以有：，

即得到数列是以公比为3的等比数列，

所以有：，

即，

当时有

故选：B

例7．（2020·全国高三三模）已知数列的前项和，其中．

（1）求数列的通项公式．

（2）若数列满足，．

证明：①数列为等差数列．

②求数列的前项和．

【答案】（1）（2）①证明见解析②

【解析】

（1）当时，，

当时，，

时，满足上式，

∴，

（2）①即，

∴，

∴为首项为，公差为的等差数列．

②∴，

∴，

∴

∴

，．

例8．（2020·上海市南洋模范中学高三三模）已知椭圆的右焦点为F(1，0)，且点在椭圆C上.

（1）求椭圆C的标准方程；

（2）过椭圆上异于其顶点的任意一点Q作圆的两条切线，切点分别为M，N(M，N不在坐标轴上)，若直线MN在x轴，y轴上的截距分别为m，n，证明：为定值；

（3）若是椭圆上不同的两点，轴，圆E过且椭圆上任意一点都不在圆E内，则称圆E为该椭圆的一个内切圆.试问：椭圆是否存在过左焦点的内切圆？若存在，求出圆心E的坐标；若不存在，请说明理由.

【答案】（1）；（2）证明见解析；（3）存在，.

【解析】（1）由题意得，.所以，

又点在椭圆上，所以 ，解，

所以椭圆的标准方程为；

（2）由（1）知，，设点

则直线的方程为——①，直线的方程为——②，

把点的坐标代入①②得,所以直线的方程为

令，得，令，得.

所以，又点在圆上.

所以，，为定值；

（3）由椭圆的对称性，不妨设，由题意知，点在轴上，

设点，则圆的方程为

由椭圆的内切圆的定义知，椭圆上的点到点的距离的最小值是，

设点是椭圆上任意一点，则，

当时，最小，所以——①

假设椭圆存在过左焦点的内切圆，则——②

又点在椭圆上，所以——③

由①②③得或，

当时，，不合题意，舍去，且经验证，符合题意，

综上，椭圆存在过左焦点的内切圆，圆心的坐标是.

【精选精练】

1．（2020·广东中山纪念中学高三三模）已知函数，若,且 ，则的取值范围为（    ）

A． B． C． D．

【答案】A

【解析】作出函数的图象，如图所示，若，且，

则当时，得，即，

则满足，

则，即，则，

设，则，

当，解得，当，解得，

当时，函数取得最小值，

当时，；

当时，，

所以，即的取值范围是，故选A.

2．（2020·南昌县莲塘第一中学高三三模）已知函数，若(互不相等)，则的取值范围是（    ）

A． B． C． D．

【答案】A

【解析】解：作出函数函数的图象，

如图，时，，令，设，则有，，所以，

所以，

因为，因为在上单调递增，所以

所以的取值范围是，

故选：A.

3．（2020·重庆高三三模）设函数若互不相等的实数满足则的取值范围是（     ）

A． B． C． D．

【答案】B

【解析】不妨设，的图像如图所示，

令，则，故或且，

所以（舎）或即且，

故，故选B.

4．（2020·河南高三三模）设，则的大小关系是（    ）

A． B． C． D．

【答案】B

【解析】设，则，

当时，，故 在为减函数，

，，则，故；

又，，即，故，

．

故选：．

5．（2020·福建漳州·高三三模）已知是定义在上的函数的导函数，且，当时，恒成立，则下列判断正确的是（    ）

A． B．

C． D．

【答案】A

【解析】构造函数，因为，所以，

则，所以的图象关于直线对称，

因为当时，，所以，

所以在上单调递增，

所以有，

即，

即，，

故选：A.

6．（2020·霍邱县第二中学高三三模）已知函数的定义域为，且满足（是的导函数），则不等式的解集为（    ）

A． B． C． D．

【答案】D

【解析】构造函数，其中，则，

所以，函数在定义域上为增函数，

在不等式两边同时乘以得，即，

所以，解得，

因此，不等式的解集为，故选D.

7．（2020·上海嘉定·高三三模）设数列的前项和为，且是6和的等差中项．若对任意的，都有，则的最小值为（    ）．

A． B． C． D．

【答案】B

【解析】由是6和的等差中项，得，令得 ，又，

得，

则是首项为，公比为的等比数列, 得．

若为奇数，；若为偶数，．

而是关于的单调递增函数，并且，，故最小值是，故此题选B．

8．（2020·安徽六安一中高三三模）已知数列前项和为.

（1）求数列的通项公式；

（2）求数列的前项和.

【答案】（1）（2）

【解析】（1）由题知=，

即，即，

，，

数列是首项为3，公比为3的等比数列，

，；

（2）由（1）知，，

，

设，       ①

  ②

①-②得，，

，，

.

9．（2020·湖南永州·高三三模）已知抛物线的焦点为，过点且斜率为的直线与抛物线交于，两点，.

（1）求抛物线的标准方程；

（2）过点的直线交抛物线于，两点.过，分别作抛物线的切线，两切线交于点，若直线与抛物线的准线交于第四象限的点，且，求直线的方程.

【答案】（1）；（2）.

【解析】解：（1）由抛物线的方程可得焦点，由题意可得直线的方程为：，即，设，，

联立直线与抛物线的方程：，

整理可得

，

由抛物线的性质可得，解得，

所以抛物线的方程为：

（2）易知直线的斜率存在且不为零，又由（1）知

故可设直线的方程为，代入抛物线的方程得，       

设，，则，，，

，

由抛物线得，则，

所以抛物线在，两点处的切线的斜率分别为，，

故两切线的方程分别为，，

即，，

解得两切线的交点为，即，

又准线的方程为，由，得

则，

由，得，得，

因为直线与准线交于第四象限的点，

故有，

从而直线的方程为.，即.

10．（2020·宝山·上海交大附中高三三模）已知椭圆的左、右焦点分别为、，长轴的一个端点与短轴两个端点组成等边三角形的三个顶点，直线l经过点，倾斜角为45°，与椭圆交于A、B两点.

（1）若，求椭圆方程；

（2）对（1）中椭圆，求的面积；

（3）M是椭圆上任意一点，若存在实数，，使得，试确定，满足的等式关系.

【答案】（1）；（2）；（3）.

【解析】（1）设椭圆的半焦距为c，由题意可得，即，

因为椭圆长轴的一个端点与短轴两个端点组成等边三角形的三个顶点，

所以，所以，所以，

所以椭圆方程为；

（2）由（1）知，，所以直线，

设，，

由消去y得，，

所以，，

所以，，

所以；

（3）由可得椭圆方程为，即，

则点，直线，

由消去y得，，

设，，

则，，

设，由可得，，

由点在椭圆上可得，

整理得，

因为

，

所以，

又，在椭圆上，所以，，

所以，

所以.

11．（2020·安徽高三三模）椭圆的离心率为，上顶点为，右焦点为，原点到直线的距离为．

（1）求椭圆的方程；

（2）直线为抛物线的准线，分别为椭圆的左、右顶点，为直线上的任一点（不在轴上），交椭圆于另一点交椭圆于另一点，求证：三点共线．

【答案】（1）；（2）证明详见解析.

【解析】（1）设，根据离心率的定义和面积相等可得方程组，解得，

因此所求的椭圆的方程为．

（2）显然，直线的方程为．设的坐标为，则直线的方程为，

把它代入椭圆的方程中，消去得．

根据一元二次方程根与系数的关系知，

因此，

同理，直线的方程为，把它代入椭圆的方程中，

消去得，

根据一元二次方程根与系数的关系知，

得，

由于，所以当时，，因此，

当时，，或易知三点共线．

所以三点共线．

12．（2020·沙坪坝·重庆一中高三三模）已知椭圆的右焦点为，离心率，点A、B分别是椭圆E的上、下顶点，O为坐标原点.

（1）求椭圆E的方程；

（2）过F作直线l分别与椭圆E交于C、D两点，与y轴交于点P，直线AC和BD交于点Q，求的值.

【答案】（1）；（2）1.

【解析】（1），，

，椭圆.

（2）易知l的斜率存在且不为0，

设，，，

由，

，设点，，

则，

由A、Q、C三点共线，，

由B、Q、D三点共线，，

上面两式相除得：，

，

结合图形易知与同号，

，

，即为定值1.