人教版新课标A必修24.2 直线、圆的位置关系导学案

这是一份人教版新课标A必修24.2 直线、圆的位置关系导学案，共7页。

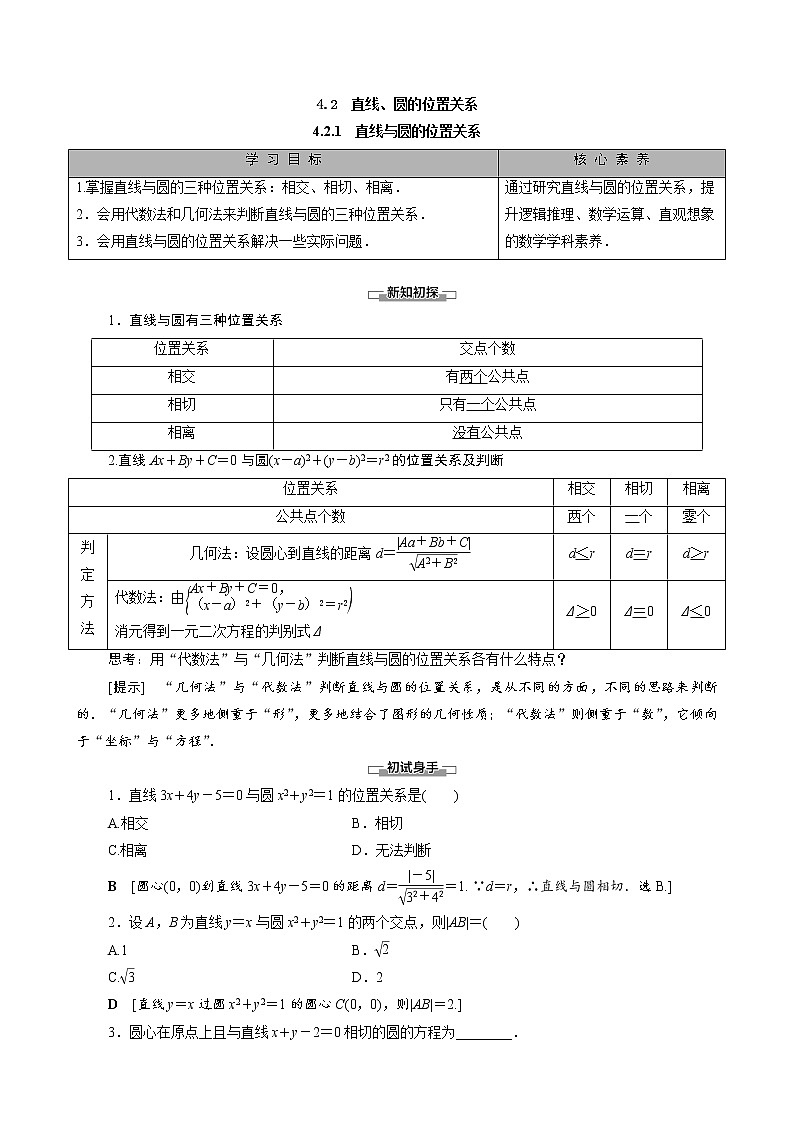
1．直线与圆有三种位置关系
2.直线Ax＋By＋C＝0与圆(x－a)2＋(y－b)2＝r2的位置关系及判断
思考：用“代数法”与“几何法”判断直线与圆的位置关系各有什么特点？
[提示] “几何法”与“代数法”判断直线与圆的位置关系，是从不同的方面，不同的思路来判断的．“几何法”更多地侧重于“形”，更多地结合了图形的几何性质；“代数法”则侧重于“数”，它倾向于“坐标”与“方程”．
1．直线3x＋4y－5＝0与圆x2＋y2＝1的位置关系是( )
A.相交 B．相切
C.相离 D．无法判断
B [圆心(0，0)到直线3x＋4y－5＝0的距离d＝ eq \f(|－5|,\r(32＋42))＝1. ∵d＝r，∴直线与圆相切．选B.]
2．设A，B为直线y＝x与圆x2＋y2＝1的两个交点，则|AB|＝( )
A.1 B． eq \r(2)
C. eq \r(3) D．2
D [直线y＝x过圆x2＋y2＝1的圆心C(0，0)，则|AB|＝2.]
3．圆心在原点上且与直线x＋y－2＝0相切的圆的方程为________．
x2＋y2＝2 [圆的半径就是原点到直线x＋y－2＝0的距离，
∴r＝d＝ eq \f(|－2|,\r(2))＝ eq \r(2).
所以所求圆的方程为x2＋y2＝2.]
4．直线x＋2y＝0被圆C：x2＋y2－6x－2y－15＝0所截得的弦长等于________．
4 eq \r(5) [由已知圆心C(3，1)，半径r＝5.又圆心C到直线l的距离d＝ eq \f(|3＋2|,\r(5))＝ eq \r(5)，则弦长＝2 eq \r(r2－d2)＝4 eq \r(5).]
直线与圆的位置关系
【例1】 已知直线方程mx－y－m－1＝0，圆的方程x2＋y2－4x－2y＋1＝0.当m为何值时，圆与直线：
(1)有两个公共点；
(2)只有一个公共点；
(3)没有公共点．
[解] 法一：将直线mx－y－m－1＝0代入圆的方程化简整理得，
(1＋m2)x2－2(m2＋2m＋2)x＋m2＋4m＋4＝0.
∵Δ＝4m(3m＋4)，
(1)∴当Δ>0时，即m>0或m