初中数学湘教版九年级上册3.4 相似三角形的判定与性质达标测试

这是一份初中数学湘教版九年级上册3.4 相似三角形的判定与性质达标测试，共10页。试卷主要包含了下列各组图形中可能不相似的是，下面一定相似的一组三角形为，∴AE＝5等内容，欢迎下载使用。
第2课时 相似三角形判定定理1
一、选择题
1.下列各组图形中可能不相似的是( )
A.各有一个角是45°的两个等腰三角形 B.各有一个角是60°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形 D.两个等腰直角三角形
2.下面一定相似的一组三角形为( )
A．两个等腰三角形 B．两个直角三角形 C．两个等腰直角三角形 D．以上都不对
3.下列条件中，一定能判定两个等腰三角形相似的是( )
A．都含有一个40°的内角 B．都含有一个50°的内角
C．都含有一个60°的内角 D．都含有一个70°的内角
4.如图，在△ABC中，∠BCD＝∠A，DE∥BC，与△ABC相似的三角形有( )
A．1个 B．2个 C．3个 D．4个

第4题图 第5题图 第6题图 第7题图
5.如图，在△ABC中，∠ADE＝∠C，则下列等式成立的是( )
A.eq \f(AD,AB)＝eq \f(AE,AC) B.eq \f(AE,BC)＝eq \f(AD,BD) C.eq \f(DE,BC)＝eq \f(AE,AB) D.eq \f(DE,BC)＝eq \f(AD,AB)
6.如图，在△ABC中，∠ACB＝90°，CD⊥AB于点D，则图中相似三角形共有( )
A．1对 B．2对 C．3对 D．0对
7.如图,E为矩形ABCD边CD的延长线上一点,BE交AD于点G,AF⊥BE于点F,则图中与△EDG相似的三角形共有( )
A.2个B.3个C.4个D.5个
8.如图,下列条件中,不能判定△ACD∽△ABC的是( )
A.∠ADC=∠ACBB.∠B=∠ACD C.∠ACD=∠BCD D.∠BDC=180°-∠ACB

第8题图 第9题图 第10题图 第11题图
9.【2020·牡丹江】如图，在矩形ABCD中，AB＝3，BC＝10，点E在BC边上，DF⊥AE，垂足为F.若DF＝6，则线段EF的长为( )
A．2 B．3 C．4 D．5
10.【2021·石家庄41中校级月考】如图，在△ABC中，∠ACB＝90°，CD⊥AB于点D，下列说法中：①AC·BC＝AB·CD；②AC2＝AD·DB；③BC2＝BD·BA；④CD2＝AD·DB.
正确的个数是( )
A．1 B．2 C．3 D．4
11.如图，已知D是△ABC的边BC上的一点，∠BAD＝∠C，∠ABC的平分线交边AC于点E，交AD于点F，那么下列结论中错误的是( )
A．△BDF∽△BEC B．△BFA∽△BEC C．△BAC∽△BDA D．△BDF∽△BAE
12.【中考·赤峰】如图，D，E分别是△ABC的边AB，AC上的点，∠ADE＝∠ACB，若AD＝2，AB＝6，AC＝4，则AE的长是( )
A．1 B．2 C．3 D．4
二、填空题
13.两角分别________的两个三角形相似；一个锐角________的两个直角三角形相似．
14.如图所示的三角形中，x＝________．

第14题图 第15题图 第16题图 第17题图
15.如图，D是△ABC的边AB上一点，连接CD，若AD＝2，BD＝4，∠ACD＝∠B，则AC的长为________．
16.【2020·乐山改编】如图，E是矩形ABCD的边CB上的一点，AF⊥DE于点F，AB＝3，AD＝2，CE＝1，则DF的长度是________．
17.如图，在△ABC中，AB＝9，AC＝6，点E在AB上，且AE＝3，点F在AC上，连接EF，若△AEF与△ABC相似，则AF＝________．
18.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E,F分别在边BC,AC上,沿EF所在的直线折叠∠C,使点C的对应点D恰好落在边AB上.若△EFC和△ABC相似,则AD的长为 .
三、解答题
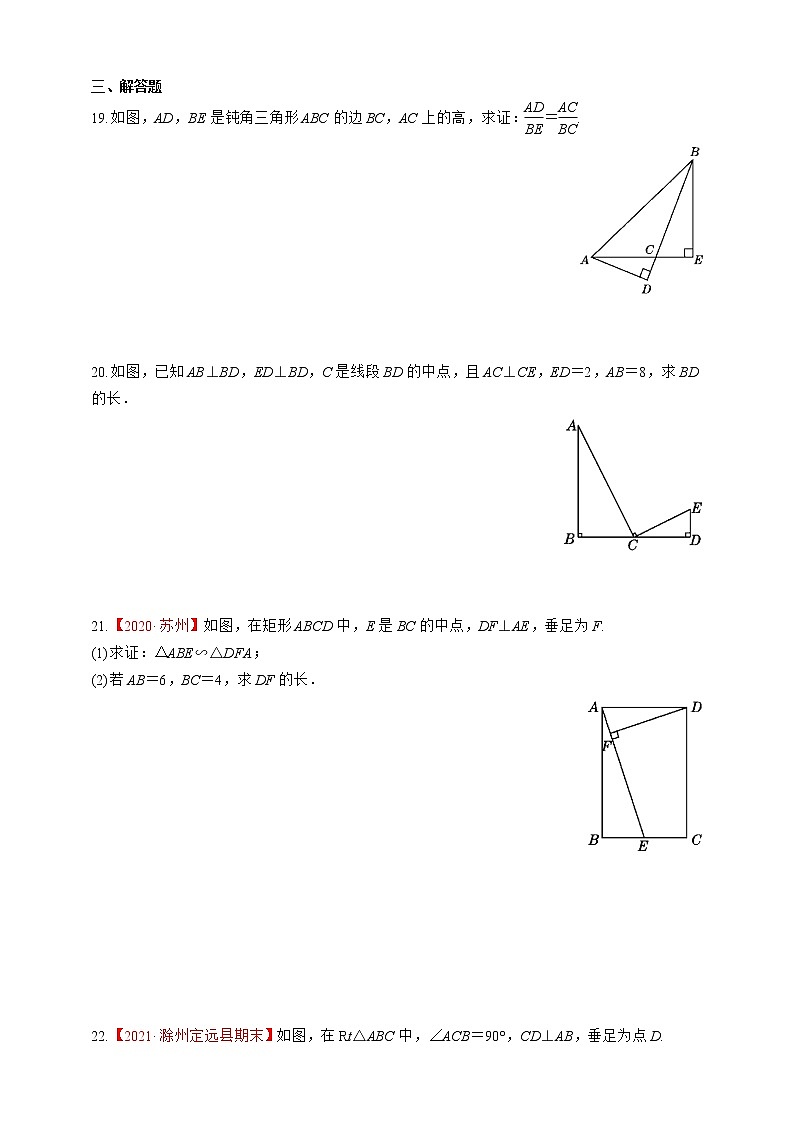
19.如图，AD，BE是钝角三角形ABC的边BC，AC上的高，求证：eq \f(AD,BE)＝eq \f(AC,BC).
20.如图，已知AB⊥BD，ED⊥BD，C是线段BD的中点，且AC⊥CE，ED＝2，AB＝8，求BD的长．
21.【2020·苏州】如图，在矩形ABCD中，E是BC的中点，DF⊥AE，垂足为F.
(1)求证：△ABE∽△DFA；
(2)若AB＝6，BC＝4，求DF的长．
22.【2021·滁州定远县期末】如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为点D.
(1)求证：BC2＝AB·DB；
(2)若AD＝6，BD＝4，求CD的长．
23.如图,平行四边形ABCD的对角线相交于点O,点E在BC边的延长线上,且OE=OB,连接DE.
(1)求证:DE⊥BE.
(2)如果OE⊥CD,求证:BD·CE=CD·DE.
24.在△ABC中，P为边AB上一点．
(1)如图①，若∠ACP＝∠B，求证：AC2＝AP·AB；
(2)M为CP的中点，AC＝2.
①如图②，若∠PBM＝∠ACP，AB＝3，求BP的长；
②如图③，若∠ABC＝45°，∠A＝∠BMP＝60°，直接写出BP的长．
参考答案
一、选择题
1.下列各组图形中可能不相似的是( A )
A.各有一个角是45°的两个等腰三角形 B.各有一个角是60°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形 D.两个等腰直角三角形
2.下面一定相似的一组三角形为( C )
A．两个等腰三角形 B．两个直角三角形 C．两个等腰直角三角形 D．以上都不对
3.下列条件中，一定能判定两个等腰三角形相似的是( C )
A．都含有一个40°的内角 B．都含有一个50°的内角
C．都含有一个60°的内角 D．都含有一个70°的内角
4.如图，在△ABC中，∠BCD＝∠A，DE∥BC，与△ABC相似的三角形有( B )
A．1个 B．2个 C．3个 D．4个

第4题图 第5题图 第6题图 第7题图
5.如图，在△ABC中，∠ADE＝∠C，则下列等式成立的是( C )
A.eq \f(AD,AB)＝eq \f(AE,AC) B.eq \f(AE,BC)＝eq \f(AD,BD) C.eq \f(DE,BC)＝eq \f(AE,AB) D.eq \f(DE,BC)＝eq \f(AD,AB)
6.如图，在△ABC中，∠ACB＝90°，CD⊥AB于点D，则图中相似三角形共有( C )
A．1对 B．2对 C．3对 D．0对
【点拨】△ABC∽△ACD，△ABC∽△CBD，△ACD∽△CBD.
7.如图,E为矩形ABCD边CD的延长线上一点,BE交AD于点G,AF⊥BE于点F,则图中与△EDG相似的三角形共有( C )
A.2个B.3个C.4个D.5个
8.如图,下列条件中,不能判定△ACD∽△ABC的是( C )
A.∠ADC=∠ACBB.∠B=∠ACD C.∠ACD=∠BCD D.∠BDC=180°-∠ACB

第8题图 第9题图 第10题图 第11题图
9.【2020·牡丹江】如图，在矩形ABCD中，AB＝3，BC＝10，点E在BC边上，DF⊥AE，垂足为F.若DF＝6，则线段EF的长为( B )
A．2 B．3 C．4 D．5
【点拨】∵四边形ABCD为矩形，
∴AD＝BC＝10，∠B＝90°，AD∥BC.
∴∠AEB＝∠DAF.
∵DF⊥AE，∴∠F＝90°＝∠B，
∴△AFD∽△EBA.∴eq \f(AD,EA)＝eq \f(DF,AB)，
即eq \f(10,AE)＝eq \f(6,3).∴AE＝5.
∵AD＝10，DF＝6，∴AF＝eq \r(102－62)＝8.
∴EF＝AF－AE＝8－5＝3.
10.【2021·石家庄41中校级月考】如图，在△ABC中，∠ACB＝90°，CD⊥AB于点D，下列说法中：①AC·BC＝AB·CD；②AC2＝AD·DB；③BC2＝BD·BA；④CD2＝AD·DB.
正确的个数是( C )
A．1 B．2 C．3 D．4
11.如图，已知D是△ABC的边BC上的一点，∠BAD＝∠C，∠ABC的平分线交边AC于点E，交AD于点F，那么下列结论中错误的是( A )
A．△BDF∽△BEC B．△BFA∽△BEC C．△BAC∽△BDA D．△BDF∽△BAE
12.【中考·赤峰】如图，D，E分别是△ABC的边AB，AC上的点，∠ADE＝∠ACB，若AD＝2，AB＝6，AC＝4，则AE的长是( C )
A．1 B．2 C．3 D．4
【点拨】∵∠ADE＝∠ACB，∠A＝∠A，
∴△ADE∽△ACB，∴eq \f(AD,AC)＝eq \f(AE,AB)，即eq \f(2,4)＝eq \f(AE,6)，解得AE＝3.
二、填空题
13.两角分别________的两个三角形相似；一个锐角________的两个直角三角形相似．
【答案】相等 相等
14.如图所示的三角形中，x＝________．

第14题图 第15题图 第16题图 第17题图
【答案】2eq \r(2)
15.如图，D是△ABC的边AB上一点，连接CD，若AD＝2，BD＝4，∠ACD＝∠B，则AC的长为________．
【点拨】在△ACD和△ABC中，∵∠ACD＝∠B，∠A＝∠A，
∴△ACD∽△ABC，∴eq \f(AC,AB)＝eq \f(AD,AC)，
∴AC2＝AD·AB＝2×(2＋4)＝12，
∴AC＝2eq \r(3).
【答案】2eq \r(3)
16.【2020·乐山改编】如图，E是矩形ABCD的边CB上的一点，AF⊥DE于点F，AB＝3，AD＝2，CE＝1，则DF的长度是________．
【答案】eq \f(\r(10),5)
17.如图，在△ABC中，AB＝9，AC＝6，点E在AB上，且AE＝3，点F在AC上，连接EF，若△AEF与△ABC相似，则AF＝________．
【错解】2
【诊断】根据题意，要使△AEF与△ABC相似，由于本题没有说明对应关系，故采用分类讨论思想．有两种可能：(1)△AEF∽△ABC，(2)△AEF∽△ACB.
【答案】2或4.5
18.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E,F分别在边BC,AC上,沿EF所在的直线折叠∠C,使点C的对应点D恰好落在边AB上.若△EFC和△ABC相似,则AD的长为 .
【答案】95或52
【提示】若△EFC与△ABC相似,分两种情况:①若△CEF∽△CBA,则EF∥AB.连接CD,由折叠得CD⊥EF,∴CD⊥AB.由勾股定理得AB=5,∴CD=BC·ACAB=125.在Rt△ADC中,AD=AC2-CD2=95.②若△CEF∽△CAB,则∠CEF=∠A.由折叠得CD⊥EF,∴∠CEF+∠DCE=90°,又∠DCE+∠DCA=90°,∴∠CEF=∠DCA=∠A,∴AD=CD,∴在Rt△ABC中,D为AB的中点,∴AD=12AB=52.
三、解答题
19.如图，AD，BE是钝角三角形ABC的边BC，AC上的高，求证：eq \f(AD,BE)＝eq \f(AC,BC).
证明：∵AD，BE是钝角三角形ABC的边BC，AC上的高，
∴∠D＝∠E＝90°.
又∵∠DCA＝∠ECB，
∴△DAC∽△EBC.
∴eq \f(AD,BE)＝eq \f(AC,BC).
20.如图，已知AB⊥BD，ED⊥BD，C是线段BD的中点，且AC⊥CE，ED＝2，AB＝8，求BD的长．
解：∵C是线段BD的中点，∴设BC＝CD＝x.
∵AB⊥BD，ED⊥BD，
∴∠B＝∠D＝90°，∠A＋∠ACB＝90°.
∵AC⊥CE，∴∠ECD＋∠ACB＝90°，
∴∠A＝∠ECD，∴△ABC∽△CDE，
∴eq \f(AB,CD)＝eq \f(BC,DE)，∴eq \f(8,x)＝eq \f(x,2)，
∴x＝4或x＝－4(舍去)，
经检验：x＝4是原方程的解．
∴BD＝2×4＝8.
21.【2020·苏州】如图，在矩形ABCD中，E是BC的中点，DF⊥AE，垂足为F.
(1)求证：△ABE∽△DFA；
证明：∵四边形ABCD是矩形，∴∠B＝90°，AD∥BC.
∴∠AEB＝∠DAF.
∵DF⊥AE，∴∠DFA＝90°.
∴∠B＝∠DFA，
∴△ABE∽△DFA.
(2)若AB＝6，BC＝4，求DF的长．
解：∵△ABE∽△DFA，∴eq \f(AB,DF)＝eq \f(AE,AD).
∵BC＝4，E是BC的中点，∴BE＝eq \f(1,2)BC＝eq \f(1,2)×4＝2.
∴在Rt△ABE中，AE＝eq \r(AB2＋BE2)＝eq \r(62＋22)＝2 eq \r(10).
又∵AD＝BC＝4，
∴eq \f(6,DF)＝eq \f(2 \r(10),4)，∴DF＝eq \f(6 \r(10),5).
22.【2021·滁州定远县期末】如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为点D.
(1)求证：BC2＝AB·DB；
证明：∵CD⊥AB，∴∠CDB＝90°.
∵∠ACB＝90°，∴∠ACB＝∠CDB.
又∵∠B＝∠B，∴ △ACB∽△CDB.
∴eq \f(AB,CB)＝eq \f(CB,DB)，∴BC2＝AB·DB.
(2)若AD＝6，BD＝4，求CD的长．
解：∵AD＝6，BD＝4，
∴AB＝AD＋DB＝10.
∴BC2＝AB·DB＝40.
在Rt△CDB中，由勾股定理，
可得CD＝eq \r(BC2－BD2)＝eq \r(40－16)＝2 eq \r(6).
23.如图,平行四边形ABCD的对角线相交于点O,点E在BC边的延长线上,且OE=OB,连接DE.
(1)求证:DE⊥BE.
(2)如果OE⊥CD,求证:BD·CE=CD·DE.
证明:(1)∵OB=OE,∴∠OEB=∠OBE.
∵四边形ABCD是平行四边形,∴OB=OD,
∴OD=OE,∴∠OED=∠ODE.
在△BED中,∠OEB+∠OBE+∠OED+∠ODE=180°,
∴∠OEB+∠OED=90°,
即∠BED=90°,∴DE⊥BE.
(2)设OE交CD于点H,
∵OE⊥CD,∴∠CHE=90°,
∴∠CEH+∠HCE=90°.
∵∠CED=90°,∴∠CDE+∠DCE=90°,
∴∠CDE=∠CEH.
∵∠OEB=∠OBE,∴∠OBE=∠CDE.
在△CED与△DEB中,∠CED=∠DEB,∠CDE=∠DBE,
∴△CED∽△DEB,∴CEDE=CDDB,即BD·CE=CD·DE.
24.在△ABC中，P为边AB上一点．
(1)如图①，若∠ACP＝∠B，求证：AC2＝AP·AB；

证明：∵∠ACP＝∠B，∠A＝∠A，
∴△ACP∽△ABC.
∴eq \f(AC,AB)＝eq \f(AP,AC).∴AC2＝AP·AB.
(2)M为CP的中点，AC＝2.
①如图②，若∠PBM＝∠ACP，AB＝3，求BP的长；
解：作CQ∥BM交AB的延长线于点Q.
∴∠PBM＝∠AQC.
∵∠PBM＝∠ACP，∴∠ACP＝∠AQC.
又∵∠PAC＝∠CAQ，∴△APC∽△ACQ.
∴eq \f(AC,AP)＝eq \f(AQ,AC).
∴AC2＝AP·AQ.
∵M为PC的中点，BM∥CQ，∴eq \f(PB,PQ)＝eq \f(PM,PC)＝eq \f(1,2).
设BP＝x，则PQ＝2x，BQ＝x，
∴22＝(3－x)(3＋x)，解得x1＝eq \r(5)，x2＝－eq \r(5)(不合题意，舍去)．
∴BP＝eq \r(5).
②如图③，若∠ABC＝45°，∠A＝∠BMP＝60°，直接写出BP的长．
解：BP＝eq \r(7)－1.