

初中数学湘教版九年级上册第3章 图形的相似综合与测试课时训练
展开一、选择题
1.下列各组长度的线段中,是成比例线段的是( )
A.2,6,5,9 B.1,3,6,4 C.1,2,3,4 D.3,2,6,1
2.在比例尺为1∶8 000 000的地图上,量得甲、乙两地间的距离为4厘米,则甲、乙两地的实际距离为( )
A.320千米 B.32千米 C.3 200千米 D.320 000千米
3.已知点C在线段AB上,且点C是线段AB的黄金分割点(AC>BC),则下列结论正确的是( )
A.AB2=AC·BC B.BC2=AC·AB C.AC=eq \f(\r(5)-1,2)BC D.BC=eq \f(3-\r(5),2)AB
4.下列说法:①位似图形都相似;②位似图形都是平移后再放大(或缩小)得到的;③直角三角形斜边上的中线与斜边的比为1:2;④两个相似多边形的面积比为4:9,则周长的比为16:81.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
5.如果△ABC和△DEF相似,A,B分别对应D,E,且AB∶DE=1∶2,那么下列等式一定成立的是( )
A.eq \f(BC,DE)=eq \f(1,2) B.eq \f(S△ABC,S△DEF)=eq \f(1,2) C.eq \f(∠A,∠D)=eq \f(1,2) D.eq \f(△ABC的周长,△DEF的周长)=eq \f(1,2)
6.△ABC和△DEF符合下列条件,其中使△ABC和△DEF不相似的是( )
A.∠A=∠D=90°,BC=8,AB=6,EF=12,DE=9
B.AB=1,AC=1.5,BC=2,DE=4,DF=2,EF=3
C.∠A=∠E,AB=2,AC=2.4,DE=3.6,EF=3
D.AB=3,AC=5,BC=7,DE=eq \r(3), DF=eq \r(5), EF=eq \r(7)
7.如图,四边形AOEF是平行四边形,点B为OE的中点,延长FO至点C,使OC=eq \f(1,3)FO,连接AB,AC,BC,则在△ABC中,S△ABO:S△AOC:S△BOC等于( )
A.6:2:1 B.3:2:1 C.6:3:2 D.4:3:2
8.如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为eq \f(\r(2),2),点A的坐标为(0,1),则点E的坐标是( )
A.(-1.4,-1.4) B.(1.4,1.4) C.(-eq \r(2),-eq \r(2)) D.(eq \r(2),eq \r(2))
第8题图 第9题图 第10题图 第11题图
9.【2020·河北】在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是( )
A.四边形NPMQ B.四边形NPMR C.四边形NHMQ D.四边形NHMR
10.【2021·宁波期末】如图,已知D、E分别为AB、AC上的点,且DE∥BC,AE=3CE,AB=8,则AD的长为( )
A.3 B.4 C.5 D.6
11.如图,在△ABC中,点D在BC上,连接AD,点E在AC上,过点E作EF∥BC,交AD于点F,过点E作EG∥AB,交BC于点G,则下列式子一定正确的是( )
A.eq \f(AE,EC)=eq \f(EF,CD) B.eq \f(EG,AB)=eq \f(EF,CD) C.eq \f(AF,FD)=eq \f(BG,GC) D.eq \f(CG,BC)=eq \f(AF,AD)
12.【中考·通辽】如图,▱ABCD的对角线AC,BD交于点O,DE平分∠ADC交AB于点E,交AC于点F,∠BCD=60°,AD=eq \f(1,2)AB,连结OE.下列结论:①S▱ABCD=AD·BD;②DB平分∠CDE;③AO=DE;④S△ADE=5S△OFE,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
第12题图 第15题图 第17题图 第18题图
二、填空题
13.已知eq \f(x,y)=eq \f(2,3),则3x=________,eq \f(y,x)=________,eq \f(x+y,y)=________,eq \f(x,x+y)=________.
14.乐器上的一根弦AB=80 cm,两个端点A,B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,若设支撑点C到端点A的距离为x cm,则得到关于x的一元二次方程的一般形式是____________________,x≈________cm.(eq \r(5)≈2.236,结果精确到0.1 cm)
15.【2019·河池】如图,以点O为位似中心,将△OAB放大后得到△OCD,OA=2,AC=3,则eq \f(AB,CD)=________.
16.有一块三角形的草地,它的一条边长为25 m,在图纸上,这条边的长为5 cm,其他两条边的长都为4 cm,则其他两条边的实际长度都是________m.
17.如图,AD是△ABC的中线,点E在AC上,BE交AD于点F,eq \f(AF,AD)=eq \f(1,4),则eq \f(AE,AC)=________.
18.如图,△ABC是一块正三角形余料,边长为120 mm,要把它加工成正方形零件,使正方形的一边QM在边BC上,其余两个顶点P、N分别在AB、AC上,则这个正方形零件的边长是_____________mm.
三、解答题
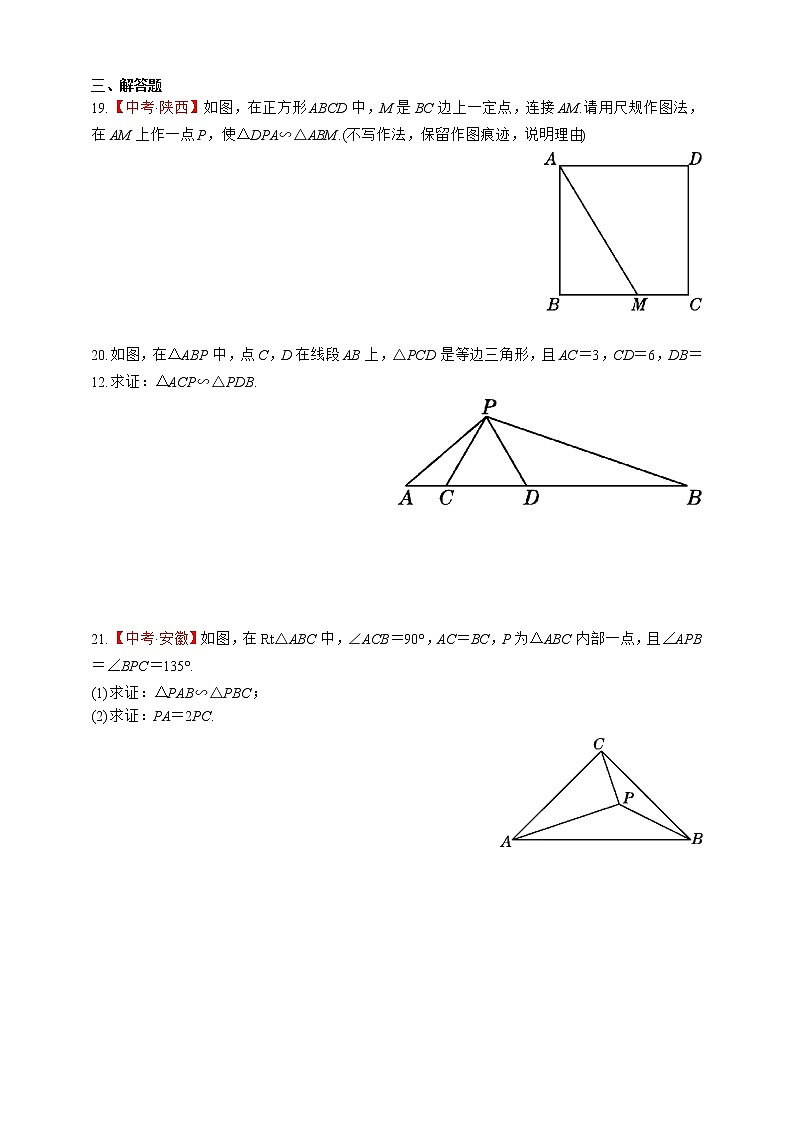
19.【中考·陕西】如图,在正方形ABCD中,M是BC边上一定点,连接AM.请用尺规作图法,在AM上作一点P,使△DPA∽△ABM.(不写作法,保留作图痕迹,说明理由)
20.如图,在△ABP中,点C,D在线段AB上,△PCD是等边三角形,且AC=3,CD=6,DB=12.求证:△ACP∽△PDB.
21.【中考·安徽】如图,在Rt△ABC中,∠ACB=90°,AC=BC,P为△ABC内部一点,且∠APB=∠BPC=135°.
(1)求证:△PAB∽△PBC;
(2)求证:PA=2PC.
22.【中考·邵阳】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.
23.如图,在Rt△ABC中,∠A=90°,AB=8,AC=6.若动点D从点B出发,沿线段BA运动到点A为止,运动速度为每秒2个单位长度.过点D作DE∥BC交AC于点E,设动点D运动的时间为x秒,AE的长为y.
(1)求出y关于x的函数表达式,并写出自变量x的取值范围;
(2)当x为何值时,△BDE的面积有最大值,最大值为多少?
24.【2021·昆明十中校级月考】如图,已知D是BC边上的中点,且AD=AC,DE⊥BC,DE与BA相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD;
(2)若S△FCD=5,BC=10,求DE的长.
参考答案
一、选择题
1.下列各组长度的线段中,是成比例线段的是( D )
A.2,6,5,9 B.1,3,6,4 C.1,2,3,4 D.3,2,6,1
2.在比例尺为1∶8 000 000的地图上,量得甲、乙两地间的距离为4厘米,则甲、乙两地的实际距离为( A )
A.320千米 B.32千米 C.3 200千米 D.320 000千米
3.已知点C在线段AB上,且点C是线段AB的黄金分割点(AC>BC),则下列结论正确的是( D )
A.AB2=AC·BC B.BC2=AC·AB C.AC=eq \f(\r(5)-1,2)BC D.BC=eq \f(3-\r(5),2)AB
4.下列说法:①位似图形都相似;②位似图形都是平移后再放大(或缩小)得到的;③直角三角形斜边上的中线与斜边的比为1:2;④两个相似多边形的面积比为4:9,则周长的比为16:81.其中正确的有( B )
A.1个 B.2个 C.3个 D.4个
5.如果△ABC和△DEF相似,A,B分别对应D,E,且AB∶DE=1∶2,那么下列等式一定成立的是( D )
A.eq \f(BC,DE)=eq \f(1,2) B.eq \f(S△ABC,S△DEF)=eq \f(1,2) C.eq \f(∠A,∠D)=eq \f(1,2) D.eq \f(△ABC的周长,△DEF的周长)=eq \f(1,2)
6.△ABC和△DEF符合下列条件,其中使△ABC和△DEF不相似的是( D )
A.∠A=∠D=90°,BC=8,AB=6,EF=12,DE=9
B.AB=1,AC=1.5,BC=2,DE=4,DF=2,EF=3
C.∠A=∠E,AB=2,AC=2.4,DE=3.6,EF=3
D.AB=3,AC=5,BC=7,DE=eq \r(3), DF=eq \r(5), EF=eq \r(7)
7.如图,四边形AOEF是平行四边形,点B为OE的中点,延长FO至点C,使OC=eq \f(1,3)FO,连接AB,AC,BC,则在△ABC中,S△ABO:S△AOC:S△BOC等于( B )
A.6:2:1 B.3:2:1 C.6:3:2 D.4:3:2
【点拨】设AB与OF相交于点M,
∵AF∥OB,
∴△FAM∽△OBM,
∴eq \f(OM,FM) =eq \f(BM,AM) =eq \f(BO,AF) =eq \f(1,2).
设S△BOM=S,则S△AOM=2S,
∵OC=eq \f(1,3)FO,OM=eq \f(1,2)FM,
∴OM=OC.
∴S△AOC=S△AOM=2S,
S△BOC=S△BOM=S.
∴S△ABO:S△AOC:S△BOC=3:2:1.
8.如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为eq \f(\r(2),2),点A的坐标为(0,1),则点E的坐标是( )
A.(-1.4,-1.4) B.(1.4,1.4) C.(-eq \r(2),-eq \r(2)) D.(eq \r(2),eq \r(2))
【点拨】∵正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为eq \f(\r(2),2),∴OA∶OD=1∶eq \r(2).
∵点A的坐标为(0,1),即OA=1,∴OD=eq \r(2).
∵四边形ODEF是正方形,∴DE=OD=eq \r(2).
∴点E的坐标为(eq \r(2),eq \r(2)).
【答案】D
第8题图 第9题图 第10题图 第11题图
9.【2020·河北】在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是( A )
A.四边形NPMQ B.四边形NPMR C.四边形NHMQ D.四边形NHMR
10.【2021·宁波期末】如图,已知D、E分别为AB、AC上的点,且DE∥BC,AE=3CE,AB=8,则AD的长为( D )
A.3 B.4 C.5 D.6
11.如图,在△ABC中,点D在BC上,连接AD,点E在AC上,过点E作EF∥BC,交AD于点F,过点E作EG∥AB,交BC于点G,则下列式子一定正确的是( C )
A.eq \f(AE,EC)=eq \f(EF,CD) B.eq \f(EG,AB)=eq \f(EF,CD) C.eq \f(AF,FD)=eq \f(BG,GC) D.eq \f(CG,BC)=eq \f(AF,AD)
12.【中考·通辽】如图,▱ABCD的对角线AC,BD交于点O,DE平分∠ADC交AB于点E,交AC于点F,∠BCD=60°,AD=eq \f(1,2)AB,连结OE.下列结论:①S▱ABCD=AD·BD;②DB平分∠CDE;③AO=DE;④S△ADE=5S△OFE,其中正确的有( B )
A.1个 B.2个 C.3个 D.4个
【点拨】∵在▱ABCD中,∠BCD=60°,∴∠ADC=120°,∠BAD=60°.∵DE平分∠ADC,∴∠ADE=∠DAE=60°=∠AED,
∴△ADE是等边三角形,∴AD=AE=DE.
∵AD=eq \f(1,2)AB,∴AE=eq \f(1,2)AB=BE,∴DE=BE,
∴∠BDE=∠DBE,∴∠BDE=eq \f(1,2)∠AED=30°,
∴∠ADB=90°,即AD⊥BD,∴S▱ABCD=AD·BD,故①正确;
∵∠CDE=60°,∠BDE=30°,∴∠CDB=∠BDE=30°,
∴DB平分∠CDE,故②正确;
∵在Rt△AOD中,AO>AD,∴AO>DE,故③错误;
∵O是BD的中点,E是AB的中点,∴OE是△ABD的中位线,
∴OE∥AD,OE=eq \f(1,2)AD,
∴∠DAF=∠FOE,∠ADF=∠OEF,
∴△OEF∽△ADF,
∴S△ADF=4S△OEF,且AF=2OF,
∴S△AEF=2S△OEF,
∴S△ADE=6S△OFE,故④错误.故选B.
第12题图 第15题图 第17题图 第18题图
二、填空题
13.已知eq \f(x,y)=eq \f(2,3),则3x=________,eq \f(y,x)=________,eq \f(x+y,y)=________,eq \f(x,x+y)=________.
【答案】2y;eq \f(3,2);eq \f(5,3);eq \f(2,5)
14.乐器上的一根弦AB=80 cm,两个端点A,B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,若设支撑点C到端点A的距离为x cm,则得到关于x的一元二次方程的一般形式是____________________,x≈________cm.(eq \r(5)≈2.236,结果精确到0.1 cm)
【答案】x2+80x-6 400=0 49.4
15.【2019·河池】如图,以点O为位似中心,将△OAB放大后得到△OCD,OA=2,AC=3,则eq \f(AB,CD)=________.
【答案】eq \f(2,5)
16.有一块三角形的草地,它的一条边长为25 m,在图纸上,这条边的长为5 cm,其他两条边的长都为4 cm,则其他两条边的实际长度都是________m.
【答案】20
17.如图,AD是△ABC的中线,点E在AC上,BE交AD于点F,eq \f(AF,AD)=eq \f(1,4),则eq \f(AE,AC)=________.
【答案】eq \f(1,7)
【点拨】如图,过点D作DG∥BE,交AC于点G.∴eq \f(AE,AG)=eq \f(AF,AD)=eq \f(1,4).
∵AD是△ABC的中线,∴BD=DC,
∴eq \f(CG,EG)=eq \f(CD,BD)=1,∴eq \f(AE,AC)=eq \f(1,7).
18.如图,△ABC是一块正三角形余料,边长为120 mm,要把它加工成正方形零件,使正方形的一边QM在边BC上,其余两个顶点P、N分别在AB、AC上,则这个正方形零件的边长是_____________mm.
【点拨】如图,作△ABC的
高AD,交PN于点E.
∵△ABC为正三角形,∴BD=eq \f(1,2)BC=60 mm,
由勾股定理得AD=eq \r(AB2-BD2)=eq \r(1202-602)=60eq \r(3)(mm).
设正方形的边长为x mm,则PN=PQ=ED=x mm,
∴AE=AD-ED=(60eq \r(3)-x)mm.
∵PN∥BC,AD⊥BC,∴AE⊥PN,△APN∽△ABC.
∴eq \f(PN,BC)=eq \f(AE,AD).即eq \f(x,120)=eq \f(60\r(3)-x,60\r(3)),解得x=240eq \r(3)-360.
∴加工成的正方形零件的边长是(240eq \r(3)-360)mm.
【答案】(240eq \r(3)-360)
三、解答题
19.【中考·陕西】如图,在正方形ABCD中,M是BC边上一定点,连接AM.请用尺规作图法,在AM上作一点P,使△DPA∽△ABM.(不写作法,保留作图痕迹,说明理由)
解:如图所示,点P即为所求.
理由:∵DP⊥AM,∴∠APD=∠ABM=90°.
∵∠BAM+∠PAD=90°,
∠PAD+∠ADP=90°,
∴∠BAM=∠ADP,∴△DPA∽△ABM.
20.如图,在△ABP中,点C,D在线段AB上,△PCD是等边三角形,且AC=3,CD=6,DB=12.求证:△ACP∽△PDB.
证明:∵△PCD是等边三角形,
∴∠PCD=∠PDC=60°,PC=CD=PD=6,
∴∠PCA=∠PDB=120°.
∵AC=3,BD=12,
∴eq \f(AC,PC)=eq \f(3,6)=eq \f(1,2),eq \f(PD,BD)=eq \f(6,12)=eq \f(1,2).
∴eq \f(AC,PC)=eq \f(PD,BD),∴△ACP∽△PDB.
21.【中考·安徽】如图,在Rt△ABC中,∠ACB=90°,AC=BC,P为△ABC内部一点,且∠APB=∠BPC=135°.
(1)求证:△PAB∽△PBC;
证明:∵∠ACB=90°,AC=BC,
∴∠ABC=45°=∠PBA+∠PBC.
又∵∠APB=135°,∴∠PAB+∠PBA=45°,
∴∠PAB=∠PBC.
又∵∠APB=∠BPC=135°,∴△PAB∽△PBC.
(2)求证:PA=2PC.
证明:∵△PAB∽△PBC,
∴PA∶PB=PB∶PC=AB∶BC.
在Rt△ABC中,AC=BC,∴AB∶BC=eq \r(2),
∴PB=eq \r(2)PC,PA=eq \r(2)PB,
∴PA=2PC.
22.【中考·邵阳】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.
解:由题意可得△DEF∽△DCA,
∴DE∶DC=EF∶AC.
∵DE=0.5米,EF=0.25米,DC=20米,
∴AC=eq \f(DC·EF,DE)=10(米),
∵BC=DG=1.5米,
∴AB=AC+BC=10+1.5=11.5(米).
答:旗杆的高度为11.5米.
23.如图,在Rt△ABC中,∠A=90°,AB=8,AC=6.若动点D从点B出发,沿线段BA运动到点A为止,运动速度为每秒2个单位长度.过点D作DE∥BC交AC于点E,设动点D运动的时间为x秒,AE的长为y.
(1)求出y关于x的函数表达式,并写出自变量x的取值范围;
解:∵DE∥BC,∴eq \f(AD,AB)=eq \f(AE,AC).
∴eq \f(8-2x,8)=eq \f(y,6).
∴y=-eq \f(3,2)x+6(0≤x≤4).
(2)当x为何值时,△BDE的面积有最大值,最大值为多少?
解:∵S△BDE=eq \f(1,2)·BD·AE=eq \f(1,2)·2x·y=eq \f(1,2)·2x·eq \b\lc\(\rc\)(\a\vs4\al\c1(6-\f(3,2)x))=-eq \f(3,2)(x-2)2+6,且-eq \f(3,2)(x-2)2≤0,∴-eq \f(3,2)(x-2)2+6≤6,∴当x=2时,S△BDE有最大值,最大值为6.
24.【2021·昆明十中校级月考】如图,已知D是BC边上的中点,且AD=AC,DE⊥BC,DE与BA相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD;
证明:如图,∵D是BC边上的中点,DE⊥BC,∴EB=EC,∴∠B=∠1.
又∵AD=AC,∴∠ACB=∠2.
∴△ABC∽△FCD.
(2)若S△FCD=5,BC=10,求DE的长.
解:如图,过点A作AM⊥CB于点M.
∵D是BC边上的中点,
∴BC=2CD.
由(1)知△ABC∽△FCD,
∴eq \f(S△ABC,S△FCD)=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(BC,CD)))eq \s\up12(2)=eq \f(4,1).
又∵S△FCD=5,∴S△ABC=20.
∵S△ABC=eq \f(1,2)BC·AM,∴AM=eq \f(2S△ABC,BC)=eq \f(2×20,10)=4.
∵DE⊥BC,AM⊥BC,∴∠EDB=∠AMB=90°.
又∵∠B=∠B,∴△BDE∽△BMA.∴eq \f(DE,AM)=eq \f(BD,BM).
由AD=AC,AM⊥BC,知DM=eq \f(1,2)CD=eq \f(1,4)BC=eq \f(5,2).
又∵BD=eq \f(1,2)BC=eq \f(1,2)×10=5,∴eq \f(DE,4)=eq \f(5,5+\f(5,2)).∴DE=eq \f(8,3).
湘教版九年级上册第3章 图形的相似综合与测试同步训练题: 这是一份湘教版九年级上册第3章 图形的相似综合与测试同步训练题,共10页。试卷主要包含了如果=,那么的值是,下列各组中的四条线段成比例的是,已知图等内容,欢迎下载使用。
湘教版数学九年级上册第3章《图形的相似》单元检测题(有答案): 这是一份湘教版数学九年级上册第3章《图形的相似》单元检测题(有答案),共10页。试卷主要包含了如果=,那么的值是,下列各组中的四条线段成比例的是,已知图等内容,欢迎下载使用。
初中数学第4章 锐角三角函数综合与测试课堂检测: 这是一份初中数学第4章 锐角三角函数综合与测试课堂检测,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













