苏科版八年级上册第四章 实数4.2 立方根课文配套课件ppt

这是一份苏科版八年级上册第四章 实数4.2 立方根课文配套课件ppt，共14页。PPT课件主要包含了2立方根，实践探索，立方根，三次方根，三次根号a，实践应用，交流与思考，思考与探索，拓展与延伸，a为任意实数等内容，欢迎下载使用。

　　现有一只体积为8cm3的正方体纸盒，它的每一条棱长是多少？
（1）在这个实际问题中，提出了怎样的一个计算问题？
（2）你能得到一个数x，使这个数的立方等于8吗？
（3）根据前面学习的经验，你觉得这一个数x可以用一个 什么数学概念来表示比较好？
学习目标：※ 理解立方根的概念，会用根号表示一个数的立方根；※ 会用立方运算求一些数的立方根；※ 能正确地应用立方根解决一些问题．
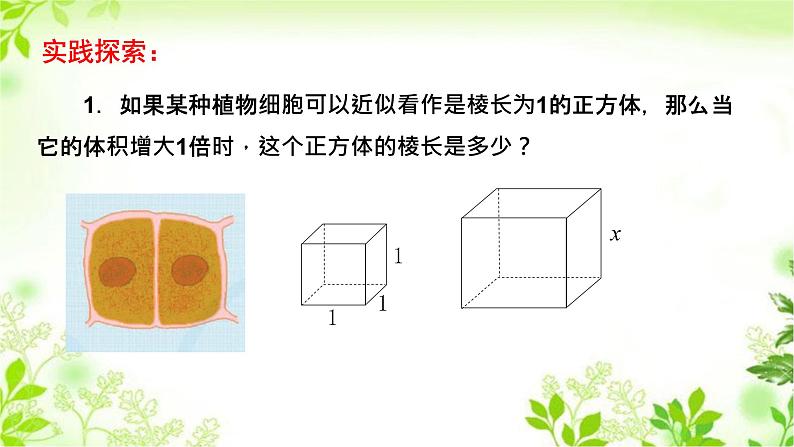
　　1．如果某种植物细胞可以近似看作是棱长为1的正方体，那么当它的体积增大1倍时，这个正方体的棱长是多少？
2．做一个正方体纸盒，如果要使正方体纸盒容积为25cm3，它的棱长是多少？
3． 想一想，你能不能从数的角度提出一个类似的问题吗？请你举个例子。
　　一般地，如果一个数的立方等于a，这个数就叫做a的　　　 ，也称为 　　　　. 也就是说，如果x3＝a，那么x叫做a的　　　 ，数a的立方根记作 ，读作“ ”. 例如：4的立方是64，所以4是64的立方根，记作　 　＝ ， 又如，x3=2，所以x是2的立方根，记作x=_________
由开平方定义同理得到：求一个数的立方根的运算叫做开立方．
开立方和立方互为逆运算，因此求一个数的立方根可以通过立方运算来求．
你能用 3 表示下列各数的立方根吗？（1）64 ；（2）－0.008 ； （3）- ?? ?? ；（4）9 ；（5）-26 ；（6）0 ．
例1：求下列各数的立方根． （1）64 ；（2）－0.008 ； （3）- ?? ?? ；（4）9 ；（5）-26 ；（6）0 ．
∵-26=-64∴-26的立方根是 ? −?? ，即-4
∵ ?? =8∴ ?? 的立方根是 ? ? ，即2
下列说法哪些是正确的，哪些不正确，为什么？ ①. 如果a是b的立方根，那么ab≥0；　 ②. ? ? 不可能是负数； ③. 一个正数的立方根一定小于这个数； ④. 一个数的立方根等于这个数本身，则这个数一定 是0和1．
例2 求下列各式中的x．
（1）x3-3=1 ?? ?? (2) (2x－1)3=125
计算下列各式的值． ? −? 3=_______ ? ?? ?=_________ ? ? ?=_________ ? ? ? =_______ ? −? ? =_________ ? ? ? =_________
想一想： ? ? 表示数a的立方根，那么( ? ? )3会表示什么呢？ ? ? ? 又表示什么呢？
通过计算你又有什么新的认识了？
立方根这个特性，我们可以表示为：当a为任何数时，( ? ? )?=? ? ? ? =a
已知：x-2的平方根是±2，2x+y+7的立方根是3。 求：x2+y2的立方根．
解：由平方根及立方根的意义可知： X-2= ±2 2 ，2x+y+7=33
1．立方根的定义与性质
2．如何求一个数的立方根（开立方）
3．立方根与平方根的区别