2020-2021学年3.7 正多边形精品练习题
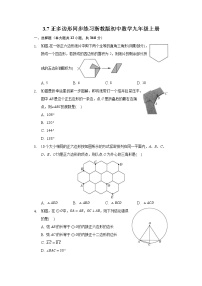
展开A.60°B.36°C.76°D.72°
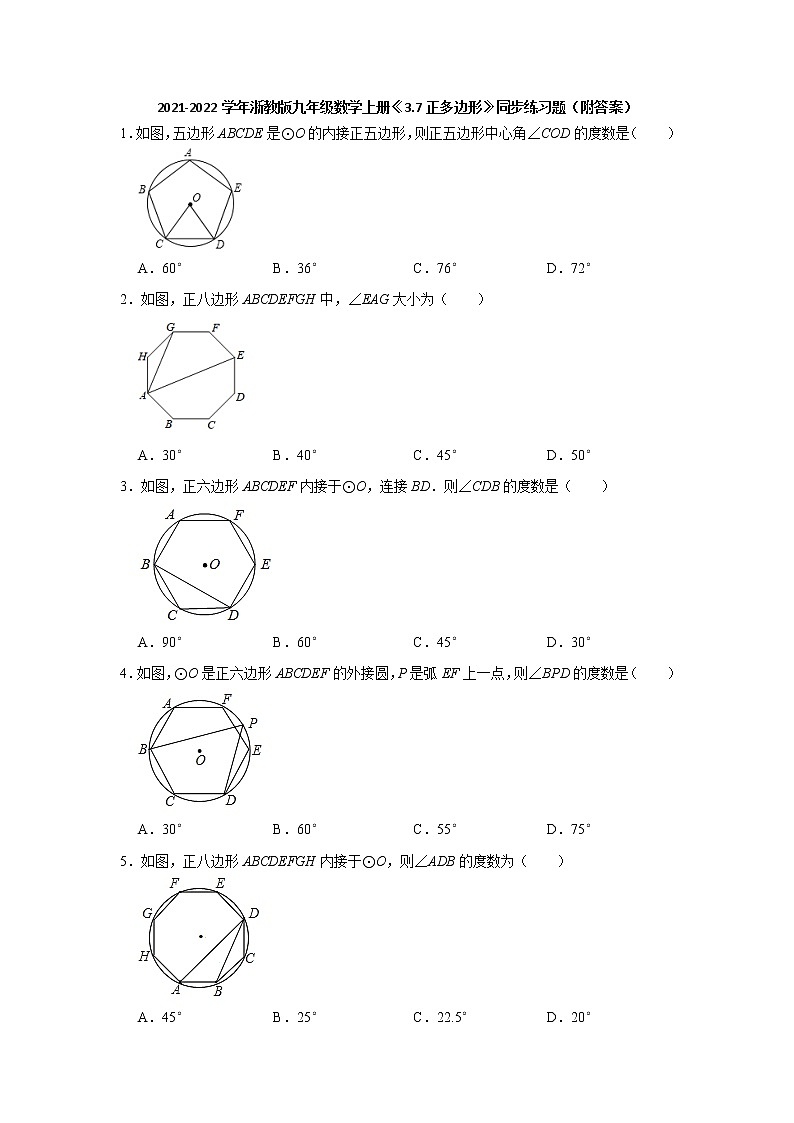
2.如图,正八边形ABCDEFGH中,∠EAG大小为( )
A.30°B.40°C.45°D.50°
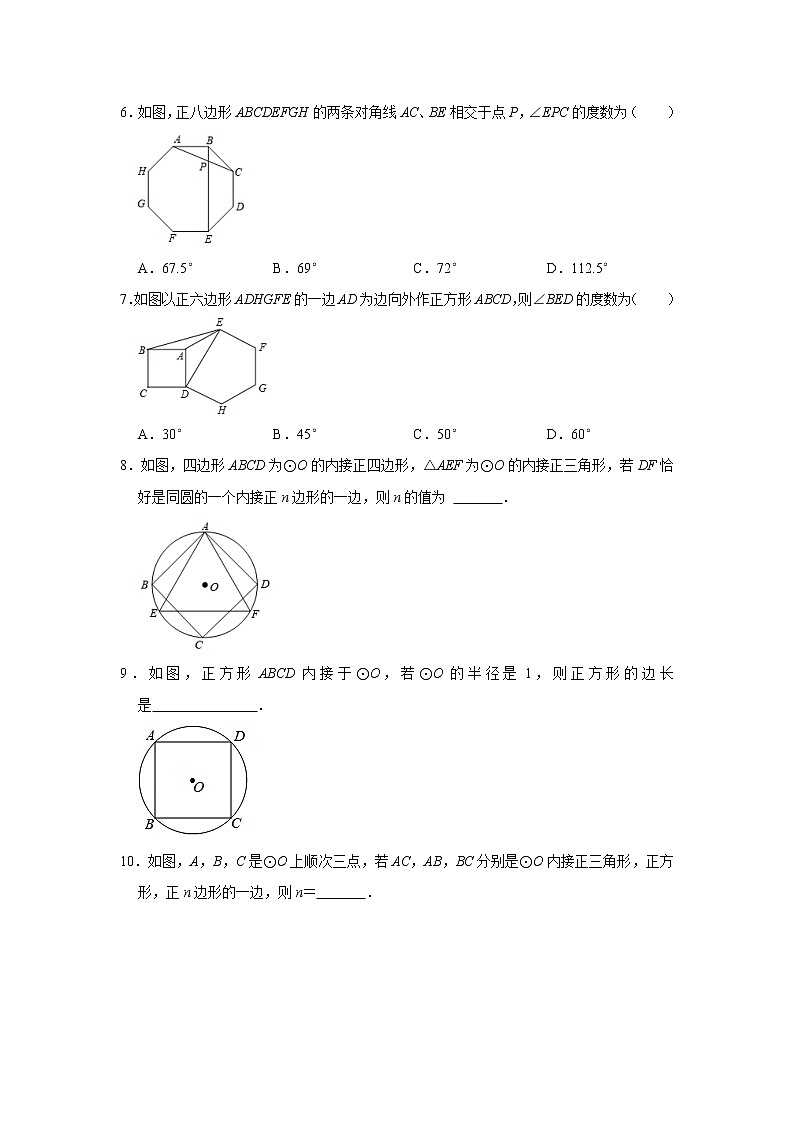
3.如图,正六边形ABCDEF内接于⊙O,连接BD.则∠CDB的度数是( )
A.90°B.60°C.45°D.30°
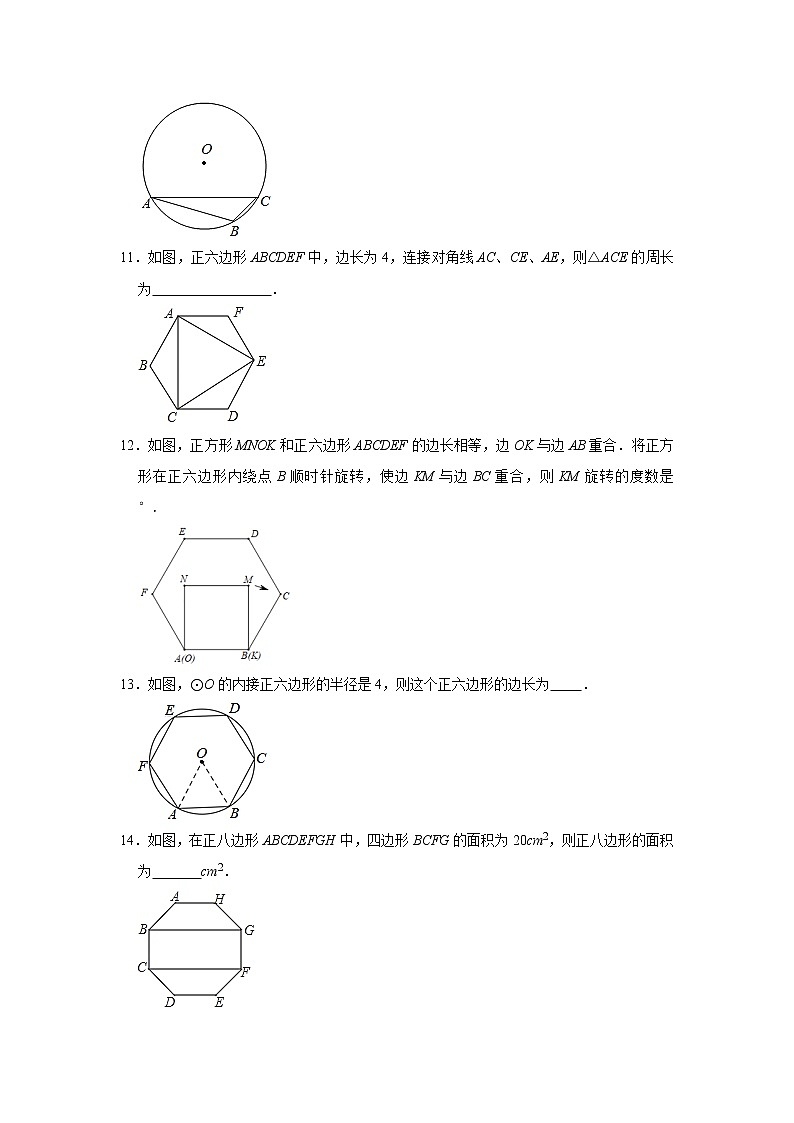
4.如图,⊙O是正六边形ABCDEF的外接圆,P是弧EF上一点,则∠BPD的度数是( )
A.30°B.60°C.55°D.75°
5.如图,正八边形ABCDEFGH内接于⊙O,则∠ADB的度数为( )
A.45°B.25°C.22.5°D.20°
6.如图,正八边形ABCDEFGH的两条对角线AC、BE相交于点P,∠EPC的度数为( )
A.67.5°B.69°C.72°D.112.5°
7.如图以正六边形ADHGFE的一边AD为边向外作正方形ABCD,则∠BED的度数为( )
A.30°B.45°C.50°D.60°
8.如图,四边形ABCD为⊙O的内接正四边形,△AEF为⊙O的内接正三角形,若DF恰好是同圆的一个内接正n边形的一边,则n的值为 .
9.如图,正方形ABCD内接于⊙O,若⊙O的半径是1,则正方形的边长是 .
10.如图,A,B,C是⊙O上顺次三点,若AC,AB,BC分别是⊙O内接正三角形,正方形,正n边形的一边,则n= .
11.如图,正六边形ABCDEF中,边长为4,连接对角线AC、CE、AE,则△ACE的周长为 .
12.如图,正方形MNOK和正六边形ABCDEF的边长相等,边OK与边AB重合.将正方形在正六边形内绕点B顺时针旋转,使边KM与边BC重合,则KM旋转的度数是 °.
13.如图,⊙O的内接正六边形的半径是4,则这个正六边形的边长为 .
14.如图,在正八边形ABCDEFGH中,四边形BCFG的面积为20cm2,则正八边形的面积为 cm2.
15.正六边形内接于半径为8的圆,则这个正六边形的面积为 .
16.一个正多边形的边长是半径的倍,则这个正多边形的边数为 .
17.一个正八边形要绕它的中心至少转 度,才能和原来的图形重合,它有 条对称轴.
18.正三边形的边长为10,则它的半径为 ,边心距为 .
19.已知圆内接正方形的边长为3,则该圆的内接正六边形边长为 .
20.某正六边形的周长为12,则其对角线的长为 cm.
21.如图.⊙O的半径为4.
(1)作圆的内接正方形ABCD;
(2)求正方形ABCD的面积.
22.如图,已知面积为8的正方形ABCD内接于⊙O,求⊙O的内接正六边形AEFCGH的面积.
23.如图,正八边形ABCDEFGH的外接圆O的半径为2,求正八边形的面积.
参考答案
1.解:∵五边形ABCDE是⊙O的内接正五边形,
∴五边形ABCDE的中心角∠COD的度数为=72°,
故选:D.
2.解:连接AC、GE、EC,如图所示:
则四边形ACEG为正方形,
∴∠EAG=45°,
故选:C.
3.解:∵在正六边形ABCDEF中,∠BOC==60°,
∴∠CDB=∠BOC=30°,
故选:D.
4.解:连接OB,OD,
∵六边形ABCDEF是正六边形,
∴∠BOD==120°,
∴∠BPD=∠BOD=60°,
故选:B.
5.解:连接OA、OB,
∵八边形ABCDEFGH是⊙O内接正八边形,
∴∠AOB==45°,
由圆周角定理得,∠ADB=∠AOB=22.5°,
故选:C.
6.解:∵八边形ABCDEFGH是正八边形,
∴∠ABC=(8﹣2)×180°÷8=135°,BA=BC,∠ABE=90°,
∴∠BAC=(180°﹣135°)÷2=22.5°,
∴∠EPC=∠APB=90°﹣∠BAC=67.5°,
故选:A.
7.解:∵正六边形ADHGFE的内角为120°,
正方形ABCD的内角为90°,
∴∠BAE=360°﹣90°﹣120°=150°,
∵AB=AE,
∴∠BEA=×(180°﹣150°)=15°,
∵∠DAE=120°,AD=AE,
∴∠AED==30°,
∴∠BED=15°+30°=45°.
故选:B.
8.解:连接OA、OD、OF,如图,
∵AD,AF分别为⊙O的内接正四边形与内接正三角形的一边,
∴∠AOD==90°,∠AOF==120°,
∴∠DOF=∠AOF﹣∠AOD=30°,
∴n==12,
故答案为:12.
9.解:连接OB,OC,则OC=OB=1,∠BOC=90°,
在Rt△BOC中,BC==.
∴正方形的边长是,
故答案为:.
10.解:如图,连接OA,OC,OB.
∵若AC、AB分别是⊙O内接正三角形、正方形的一边,
∴∠AOC=120°,∠AOB=90°,
∴∠BOC=∠AOC﹣∠AOB=30°,
由题意得30°=,
∴n=12,
故答案为:12.
11.解:作BG⊥AC,垂足为G.如图所示:
则AC=2AG,
∵AB=BC,
∴AG=CG,
∵六边形ABCDEF是正六边形,
∴∠ABC=120°,AB=BC=4,
∴∠BAC=30°,
∴AG=AB•cs30°=4×=2,
∴AC=2×2=4,
∴△ACE的周长为3×4=12.
故答案为12.
12.解:∵∠ABC=120°,∠OKM=90°,
∴∠MBC=120°﹣90°=30°,
故答案为:30;
13.解:如图所示,连接OA、OB
∵多边形ABCDEF是正六边形,
∴∠AOB=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=OB=4
故答案为4
14.解:连接HE,AD,
在正八边形ABCDEFGH中,可得:HE⊥BG于点M,AD⊥BG于点N,
∵正八边形每个内角为:=135°,
∴∠HGM=45°,
∴MH=MG,
设MH=MG=x,
则HG=AH=AB=GF=x,
∴BG×GF=2(+1)x2=20,
四边形ABGH面积=(AH+BG)×HM=(+1)x2=10,
∴正八边形的面积为:10×2+20=40(cm2).
故答案为:40.
15.解:设O是正六边形的中心,AB是正六边形的一边,OC是边心距,
∠AOB=60°,OA=OB=8cm,
则△OAB是正三角形,
∵OC=8×=4(cm),
∴S△OAB=AB•OC=×8×4=16(cm2),
∴正六边形的面积为16×6=96(cm2).
故答案为:96cm2.
16.解:如图所示:
AB为正多边形的一条边长,连接OA、OB,
根据题意得:AB=OA,
∴AB2=2OA2=OA2+OB2,
∴△AOB是直角三角形,∠AOB=90°,
∵=4,
∴这个正多边形的边数为4;
故答案为:4.
17.解:∵正八边形的中心角==45°,
∴正八边形要绕它的中心至少旋转45°,才能和原来的图形重合,它有8条对称轴;
故答案为:45,8.
18.解:如图所示,过点O作OD⊥BC于点D,
∵OB=OC,
∴BD=CD=BC=5.
∵∠BOC==120°,
∴∠DOC=60°,
∴OC=,OD=.
故答案为:,.
19.解:如图所示:连接OA、OB,OM、OH,
∵四边形ABCD是圆内接正方形,
∴∠AOB=90°;
∵OA=OB,
∴△AOB是等腰直角三角形,
∴∠OBA=45°,
∴AO=,
∵六边形EFGHMN是圆的内接正六边形,
∴∠MOH==60°,
∵OM=OH,
∴△OMH是等边三角形,
∴MH=OM=OA=,
即该圆的内接正六边形的边长为.
故答案为:.
20.解:如图所示,
①过点F作FG⊥AE于点G,
∵多边形ABCDEF是正六边形,
∴∠AFE=120°,AF=EF,
∴FG是AE的垂直平分线,∠GAF=30°,
∴AG=,
∴AE=2AG=2;
②过点B,C分别作BM⊥AD,CN⊥AD于点M,N两点,
∵AB=2,∠ABM=30°,
∴AM=1,
同理DN=1,
MN=BC=2,
∴AD=4,
故答案为:2或4.
21.解:(1)圆的内接正方形ABCD如图所示;
(2)∵⊙O的半径为4,
∴⊙O的直径为8,
∴正方形ABCD的面积=×8×8=32.
22.解:连接OC、OD、OG,作OM⊥CG于M,如图所示:
根据题意得:CD2=8,△OCD是等腰直角三角形,△COG是等边三角形,
∴CD=2,CG=OC,
∴OC=CD=2,
∴CG=2,CM=1,
∴OM=,
∴正六边形AEFCGH的面积=6××2×=6.
23.解:连接AO,BO,CO,AC,
∵正八边形ABCDEFGH的外接圆O半径为2,
∴AO=BO=CO=2,∠AOB=∠BOC==45°,
∴∠AOC=90°,
∴AC=2,此时AC与BO垂直,
∴S四边形AOCB=×BO×AC=×2×2=2,
∴正八边形面积为:2×4=8.
浙教版九年级上册3.7 正多边形同步测试题: 这是一份浙教版九年级上册3.7 正多边形同步测试题,共10页。试卷主要包含了【新独家原创】【尺规作图】等内容,欢迎下载使用。
初中浙教版3.7 正多边形精品练习: 这是一份初中浙教版3.7 正多边形精品练习,共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
浙教版九年级上册3.7 正多边形课后作业题: 这是一份浙教版九年级上册3.7 正多边形课后作业题,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。