2020-2021学年4 探索三角形相似的条件精品巩固练习

这是一份2020-2021学年4 探索三角形相似的条件精品巩固练习，共17页。

2021-2022学年北师大版九年级数学上册《4.4探索三角形相似的条件》同步测评（附答案）
一．选择题（共7小题，满分28分）
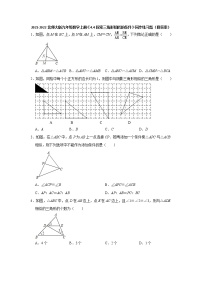
1．如图所示，直线y＝x﹣1与x轴交于A，与y轴交于B，在第一象限内找点C，使△AOC与△AOB相似，则共能找到的点C的个数（　　）

A．1 B．2 C．3 D．4
2．如图，在四边形ABCD中，已知∠ADC＝∠BAC，那么补充下列条件后不能判定△ADC和△BAC相似的是（　　）

A．CA平分∠BCD B． C．AC2＝BC•CD D．∠DAC＝∠ABC
3．如图，△ABC中，P为边AB上一点，下列选项中的条件，不能说明△ACP与△ACB相似的是（　　）

A．∠ACP＝∠B B．∠APC＝∠ACB
C．AC2＝AP×AB D．AB×CP＝BC×AC
4．如图，△ABC中，CE⊥AB，垂足为E，BD⊥AC，垂足为点D，CE与BD交于点F，则图中相似三角形有几对（　　）

A．6对 B．5对 C．4对 D．3对
5．如图，D是△ABC边AB上一点，添加一个条件后，仍不能使△ACD∽△ABC的是（　　）

A．∠ACD＝∠B B．∠ADC＝∠ACB C．AC2＝AD•AB D．
6．如图，△ABC的两条中线BE，CD交于点O，则下列结论不正确的是（　　）

A．＝ B．＝
C．△ADE∽△ABC D．S△DOE：S△BOC＝1：2
7．如图，在△ABC中，点P在边AB上，则在下列四个条件中：①∠ACP＝∠B；②∠APC＝∠ACB；③AC2＝AP•AB；④AB•CP＝AP•CB，不能判定△APC与△ACB相似的是（　　）

A．① B．② C．③ D．④
二．填空题（共6小题，满分24分）
8．在△ABC中，AB＝6cm，AC＝9cm，动点D从点B开始沿BA边运动，速度为1cm/s；动点E从点A开始沿AC边运动，速度为2cm/s．如果D，E两动点同时运动，那么当它们运动 　 　s时，由D，A，E三点连成的三角形与△ABC相似．


9．如图，在Rt△ABC中，∠C＝90°，AB＝10，BC＝6，点E，F分别在边BC，AC上，沿EF所在的直线折叠∠C，使点C的对应点D恰好落在边AB上，若△EFC和△ABC相似，则AD的长为 　 　．

10．在△ABC中，AB＝4，BC＝5，AC＝6．如果DE＝10．那么当EF＝　 　，DF＝　 　时，△ABC∽△DEF．
11．△ABC的三边长分别为7、6、2，△A'B'C'的两边长分别为1、3，要使△ABC∽△A'B'C'，则△A'B'C'的第三边长应为 　 　．
12．如图，在△ABC中，AB＝4，BC＝8，点D从点A开始沿AB边向点B以1个单位/秒的速度移动，点E从点B开始沿BC边向点C以2个单位/秒的速度移动，如果D，E分别从A，B同时出发，经过 　 　秒后，△DBE与△ABC相似．

13．如图，在矩形ABCD中，E，F分别是CD，BC上的点，∠AEF＝90°，有以下结论：①△ADE∽△AEF；②△ECF∽△AEF；③△ADE∽△ECF；④△AEF∽△ABF；⑤△ADE∽△ABF，其中正确的是 　 　（把你认为正确的序号都填上）．

三．解答题（共11小题，满分68分）
14．如图，AB⊥BD，CD⊥BD，AB＝12，CD＝8，BD＝28，点P在BD上移动，当以P，C，D为顶点的三角形与△ABP相似时，求PB的长．

15．如图，在等边△ABC中，P为BC上一点，D为AC上一点，且∠APD＝60°．求证：△ABP∽△PCD．

16．已知：如图，在△ABC中，∠C＝90°，AB＝10cm，BC：AC＝4：3，点P从点B出发，沿BC向点C以2cm/s的速度移动，点Q从C点出发沿CA向点A以1cm/s的速度移动，如果P、Q分别从B、C同时出发，经过多少秒时以C、P、Q三点组成的三角形与△CBA相似？

17．如图，在△ABC中，∠B＝90°，AB＝5cm，BC＝7cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，同时点Q从点B开始沿BC向点C以2cm/s的速度移动．当一个点到达终点时另一点也随之停止运动，设运动时间为x秒（x＞0）．
（1）当x＝　 　秒时，PQ的长度等于5cm；
（2）运动过程中，△PQB的面积能否等于8cm2？说明理由．
（3）当x为何值时，以P，B，Q为顶点的三角形与△ABC相似？

18．如图，在△ABC中，AD平分∠BAC，E是AD上一点，且BE＝BD；求证：△ABE∽△ACD．

19．如图，在Rt△ABC中，∠C＝90°，AC＝6cm，BC＝8cm，点P从点A出发，向终点C边以1cm/s的速度运动，点Q从点C出发，沿着终点B边以2cm/s的速度运动，且当其中一点到达终点时，另一点也随之停止移动．
（1）如果P与Q同时出发，经过多少秒后，可以使△PQC的面积为Rt△ABC面积的三分之一．
（2）如果P与Q同时出发，经过多少秒后，可以使△PQC和△ABC相似．

20．如图，已知∠1＝∠2＝∠3，求证：△ABC∽△ADE．

21．如图，在Rt△ABC中，∠C＝90°，AC＝6cm，BC＝8cm，点P从点A出发，沿AC向点C以1cm/s的速度移动，点Q从点C出发，沿CB向点B以2cm/s的速度移动，当其中一点到达终点时，另一点也随之停止移动．
（1）问点P、Q同时出发，几秒后可使PQ的长为？
（2）问点P、Q同时出发，几秒后可使△PCQ与△ACB相似？




22．如图，在△ABC中，AB＝AC，点D、E分别在边BC、边AB上，且∠ADE＝∠B，求证：△ADC∽△DEB．

23．如图，Rt△ABC，∠C＝90°，AC＝10cm，BC＝8cm．点P从点C出发，以2cm/s的速度沿CA向点A匀速运动，同时点Q从点B出发，以1cm/s的速度沿BC向点C匀速运动，当一个点到达终点时，另一个点随之停止．
（1）求经过几秒后，△PCQ的面积等于16cm2？
（2）经过几秒，△PCQ与△ABC相似？

24．如图，AD、CE是△ABC的高，AD与CE相交于点F，连接ED．
（1）求证：△ABD∽△CBE；
（2）求证：△ABC∽△DBE．


参考答案
一．选择题（共7小题，满分28分）
1．解：∵点C在第一象限，
∴当点C为直角顶点时，有两种情形，
当点A为直角顶点时，也有两种情形，共有4种情形．
故选：D．

2．解：在△ADC和△BAC中，∠ADC＝∠BAC，
如果△ADC∽△BAC，需满足的条件有：
①∠DAC＝∠ABC或AC是∠BCD的平分线；
②＝；
故选：C．
3．解：A、当∠ACP＝∠B，∠A＝∠A时，△APC∽△ACB，故本选项不符合题意；
B、当∠APC＝∠ACB，∠A＝∠A时，△APC∽△ACB，故本选项不符合题意；
C、当AC2＝AP•AB，即AC：AB＝AP：AC时，结合∠A＝∠A可以判定△APC∽△ACB，故本选项不符合题意；
D、当AB×CP＝AP×AC时，不能判断△APC和△ACB相似．
故选：D．
4．解：∵BD⊥AC，CE⊥AB，
∴∠AEC＝∠ADB＝90°，∠BEF＝∠CDF＝90°，
∵∠A＝∠A，∠EFB＝∠DFC，
∴△AEC∽△ADB，△BEF∽△CDF，
∵∠EBF＝∠ABD，∠BEF＝∠ADB＝90°，
∴△BEF∽△BDA∽△CEA∽△CDF，
∴共有6对相似三角形，
故选：A．
5．解：A、当∠ACD＝∠B时，再由∠A＝∠A，可得出△ACD∽△ABC，故此选项不合题意；
B、当∠ADC＝∠ACB时，再由∠A＝∠A，可得出△ACD∽△ABC，故此选项不合题意；
C、当AC2＝AD•AB时，即＝，再由∠A＝∠A，可得出△ACD∽△ABC，故此选项不合题意；
D、当＝时，无法得出△ACD∽△ABC，故此选项符合题意．
故选：D．
6．解：∵AD＝DB，AE＝EC，
∴DE＝BC，DE∥BC，
∴＝，A选项结论正确，不符合题意；
∵DE∥BC，
∴＝，B选项结论正确，不符合题意；
∵DE∥BC，
∴△ADE∽△ABC，C选项结论正确，不符合题意；
∵DE∥BC，
∴△DOE∽△COB，
∴S△DOE：S△COB＝1：4，D选项结论错误，符合题意；
故选：D．
7．解：①、当∠ACP＝∠B，
∵∠A＝∠A，
∴△APC∽△ACB，
∴①不符合题意；
②、当∠APC＝∠ACB，
∵∠A＝∠A，
∴△APC∽△ACB，
∴②不符合题意；
③、当AC2＝AP•AB，
即AC：AB＝AP：AC，
∵∠A＝∠A
∴△APC∽△ACB，
∴③不符合题意；
④、∵当AB•CP＝AP•CB，即PC：BC＝AP：AB，
而∠PAC＝∠CAB，
∴不能判断△APC和△ACB相似，
∴④符合题意；
故选：D．
二．填空题（共6小题，满分24分）
8．解：根据题意得：AE＝2t，BD＝t，
∴AD＝6﹣t，
∵∠A＝∠A，
∴分两种情况：
①当＝时，
即＝，解得：t＝；
②当＝时，
即＝，解得：t＝；
综上所述：当t＝或时，△ADE与△ABC相似．
9．解：∵∠C＝90°，AB＝10，BC＝6，
∴AC＝8，
∴AC：BC＝4：3
若△CEF与△ABC相似，分两种情况：
①若CF：CE＝4：3，
∵AC：BC＝4：3，
∴CF：CE＝AC：BC，
∴EF∥AB．
连接CD，如图1所示：

由折叠性质可知，CD⊥EF，
∴CD⊥AB，即此时CD为AB边上的高．
在Rt△ABC中，
，
∴AD＝；
②若CF：CE＝3：4，
∵AC：BC＝4：3，∠C＝∠C，
∴△CEF∽△CAB，
∴∠CEF＝∠A．
连接CD，如图2所示：

由折叠性质可知，∠CEF+∠ECD＝90°，
又∵∠A+∠B＝90°，
∴∠B＝∠ECD，
∴BD＝CD．
同理可得：∠A＝∠FCD，AD＝CD，
∴D点为AB的中点，
∴AD＝AB＝5；
故答案为：或5．
10．解：当EF＝，DF＝15时，△ABC∽△DEF，
理由如下：∵，＝，＝，
∴，
∴△ABC∽△DEF，
故答案为：，15．
11．解：设△A′B′C′的第三边为x，
∵△ABC∽△A′B′C′，△ABC的三边长分别为7、6、2，△A′B′C′的两边长分别为1、3，
∴1：2＝3：6＝x：7，
解得：x＝．
故答案为：．
12．解：设经过x秒后，△DBE与△ABC相似，
则BD＝AB﹣AD＝4﹣x，BE＝2x，
由于∠C＝∠C，
故：（1）当BD与AB是对应边时，＝，
即＝，
解得x＝2；
（2）当BP与BC是对应边时，＝，
即＝，
解得x＝，
故经过或2秒后，△PBQ与△ABC相似，
故答案为：或2．
13．解：在矩形ABCD中，
∵∠D＝∠C＝90°，∠AEF＝90°，
∴∠DEA+∠CEF＝90°，∠DEA+∠DAE＝90°，
∴∠DAE＝∠CEF，
∴△ADE∽△ECF，
其余都不符合相似的条件．
故答案为：③．
三．解答题（共11小题，满分68分）
14．解：设DP＝x，则BP＝BD﹣x＝14﹣x，
∵AB⊥BD于B，CD⊥BD于D，
∴∠B＝∠D＝90°，
∴当＝时，△ABP∽△CDP，即＝，
解得x＝，
经检验x＝是分式方程的解，
BP＝28﹣＝16.8；
当＝时，△ABP∽△PDC，即＝，
解得x1＝4，x2＝24，
经检验，x＝4或24是分式方程的解，
BP＝28﹣4＝24，BP＝28﹣24＝4，
∴当BP为16.8或4或24时，以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似．
15．证明：∵△ABC是等边三角形，
∴AB＝BC＝AC，∠B＝∠C＝60°，
∵∠BPA+∠APD+∠DPC＝180°，且∠APD＝60°，
∴∠BPA+∠DPC＝120°，
∵∠DPC+∠C+∠PDC＝180°，
∴∠DPC+∠PDC＝120°，
∴∠BPA＝∠PDC，
∴△ABP∽△PCD．
16．解：设BC＝4x，AC＝3x，，
由勾股定理得：AC2+BC2＝AB2，
∴（3x）2+（4x）2＝102，
解得：x＝2（负值舍去），
∴AC＝6，BC＝8，
设经过x秒时，以C、P、Q为顶点的三角形恰与△ABC相似，
∵∠C＝∠C＝90°，
要使以C、P、Q为顶点的三角形恰与△ABC相似，
∴或，
代入得：或，
解得：x＝2.4或x＝，
答：经过2.4秒或秒时，以C、P、Q为顶点的三角形恰与△ABC相似．
17．解：（1）当PQ＝5时，在Rt△PBQ中，∵BP2+BQ2＝PQ2，
∴（5﹣x）2+（2x）2＝52，
5x2﹣10x＝0，
x（5x﹣10）＝0，
x1＝0（舍去），x2＝2，
∴当x＝2时，PQ的长度等于5cm．
故答案为：2．
（2）设经过x秒以后△PBQ面积为8，
×（5﹣x）×2x＝8，
整理得：x2﹣5x+8＝0，
△＝25﹣32＝﹣7＜0，
∴△PQB的面积不能等于8cm2．

（3）当＝或＝时，△PBQ与△ABC相似，
∴＝或＝，
解得x＝或．
∴x的值为或时，△PBQ与△ABC相似，

18．证明：∵AD平分∠BAC，
∴∠BAD＝∠CAD．
∵BE＝BD，
∴∠BED＝∠BDE．
∴∠AEB＝∠ADC．
∴△ABE∽△ACD．
19．解：（1）∵∠C＝90°，AC＝6cm，BC＝8cm，
∴＝＝24（cm2），
∵△PQC的面积为Rt△ABC面积的三分之一，
∴△PCQ的面积为8cm2，
设xs后，可使△PCQ的面积为8cm2．
由题意得，AP＝xcm，PC＝（6﹣x）cm，CQ＝2xcm，
则（6﹣x）•2x＝8，
整理得x2﹣6x+8＝0，
解得x1＝2，x2＝4．
所以P、Q同时出发，2s或4s后可使△PCQ的面积为Rt△ABC面积的三分之一．
（2）设t秒后以P、C、Q为顶点的三角形与△ABC相似，则PC＝（6﹣t）cm，CQ＝2tcm．
当△PCQ∽△ACB时，，
即，
解得：t＝．
当△PCQ∽△BCA时，，
即，
解得：t＝．
综上所述，经过秒或秒时，以P、C、Q为顶点的三角形与△ABC相似．
20．证明：∵∠1＝∠2，
∴∠1+∠CAD＝∠2+∠CAD，
即∠BAC＝∠DAE，
∵∠1＝∠3，∠AFB＝∠CFD，
∴∠B＝∠D，
在△ABC和△ADE中，
∵∠BAC＝∠DAE，∠B＝∠D，
∴△ABC∽△ADE．
21．解：（1）设t秒后，可使PQ的长为4cm，则AP＝tcm，CQ＝2tcm，
∵PC＝AC﹣AP，
∴PC＝（6﹣t）cm，
根据勾股定理得：（6﹣t）2+（2t）2＝（4）2，解得：t＝2或t＝，
∴2秒或秒后可使PQ的长为4．
（2）设t秒后可使△PCQ∽△ACB，则PC＝（6﹣t）cm，CQ＝2tcm，
当△PCQ∽△ACB时，，即，
解得：t＝．
∴秒后可使△PCQ∽△ACB．
22．证明：在△ABC中，AB＝AC，
∴∠B＝∠C，
∵∠EDC＝∠ADE+∠ADC＝∠B+∠BED，∠ADE＝∠B，
∴∠DEB＝∠ADC，
在△ADC和△DEB中，∠ADC＝∠DEB，∠C＝∠B，
∴△ADC∽△DEB．
23．解：（1）设经过x秒，△PCQ的面积等于16cm2，
•2x•（8﹣x）＝16，
解得：x1＝x2＝4，
答：经过4秒后，△PCQ的面积等于16cm2；
（2）设经过t秒，△PCQ与△ABC相似，
因为∠C＝∠C，
所以分为两种情况：①，
∴，
解得：t＝；
②，
∴，
解得：t＝；
答：经过秒或秒时，△PCQ与△ABC相似．
24．（1）证明：∵AD、CE是△ABC的高，
∴∠ADB＝∠CEB＝90°，
∵∠B＝∠B，
∴△ABD∽△CBE．
（2）证明：∵△ABD∽△CBE，
∴＝，
∴＝，
∵∠B＝∠B，
∴△ABC∽△DBE．