苏科版八年级上册1.3 探索三角形全等的条件集体备课ppt课件

这是一份苏科版八年级上册1.3 探索三角形全等的条件集体备课ppt课件，共13页。PPT课件主要包含了你还记得吗，什么叫全等三角形，议一议，探索活动，变式拓展，ABAC，AEAC等内容，欢迎下载使用。

两个能完全重合的三角形叫做全等三角形。
全等三角形的对应边、对应角有什么重要性质？
全等三角形的对应边相等，对应角相等。
已知△ABC≌ △A’B’C’， △ABC的周长为10cm，AB=3cm，BC=4cm，则：A’B’= cm,B’C’= cm ,A’C’= cm.
我们知道：如果两个三角形全等，那么他们的对应边相等，对应角相等。反过来，两个三角形具备什么条件，即它们有多少组边或角分别相等时就全等？
1.当两个三角形只有1组边或角相等时，它们全等吗？
2.当两个三角形只有2组边或角相等时， 它们全等吗？
3.当两个三角形有3组边或角相等时， 它们全等吗？
（二）如图，用一张长方形纸剪一个直角三角形，怎么才能使全班同学剪下的直角三角形全等？
⑴任意剪一个直角三角形，同学们剪得的三角形全等吗？
⑵重新剪一个直角三角形，使全班同学剪下的都全等，说说你的方法
⑶剪下直角三角形，小组同学之间验证一下
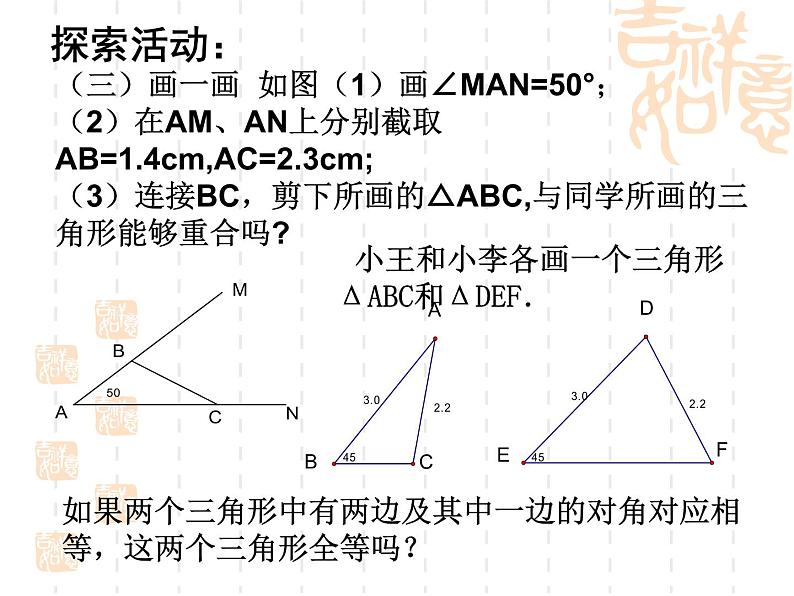
（三）画一画 如图（1）画∠MAN=50°；（2）在AM、AN上分别截取AB=1.4cm,AC=2.3cm;（3）连接BC，剪下所画的△ABC,与同学所画的三角形能够重合吗?
小王和小李各画一个三角形ΔABC和ΔDEF．
如果两个三角形中有两边及其中一边的对角对应相等，这两个三角形全等吗？
（四）按下列作法，用直尺和圆规作△ABC，使 ∠A＝∠α，AB＝a，AC＝b．
作法：1．作∠MAN ＝∠α．2．在射线AM、AN上分别作线段AB＝a，AC＝b ．3．连接BC，△ABC就是所求作的三角形．
三角形全等判定定理（一） 两边和它们的夹角对应相等的两个三角形全等，简写成“边角边”或“SAS”。
例1：如图，AB=AD,∠BAC=∠DAC，⊿ABC与⊿ADC全等吗？为什么？
如图，AB ＝AD，∠BAC ＝∠DAC.
（1）DC ＝BC 吗？
（2）CA平分∠DCB吗？
（3）本例包含哪一种图形变换？
已知：AB=AC，E、F分别在AB、AC上且AE=AF求证：⊿ABF≌⊿ACE
审题： ， 。
审图： 。
∠A是⊿ABF与⊿ACE的公共角
审结论：⊿ABF≌⊿ACE SAS
证明： 在⊿ABF和⊿ACE中 AB=AC （已知） ∠A= ∠A（公共角） AE=AC（已知） ∴ ⊿ABF≌⊿ACE （SAS）
如图，△ABC中，AB＝AC，AD平分∠BAC，试说明△ABD≌△ACD. AD与BC有怎样的位置关系