考点17 正余弦定理（讲解）（解析版）练习题

考点17  正余弦定理

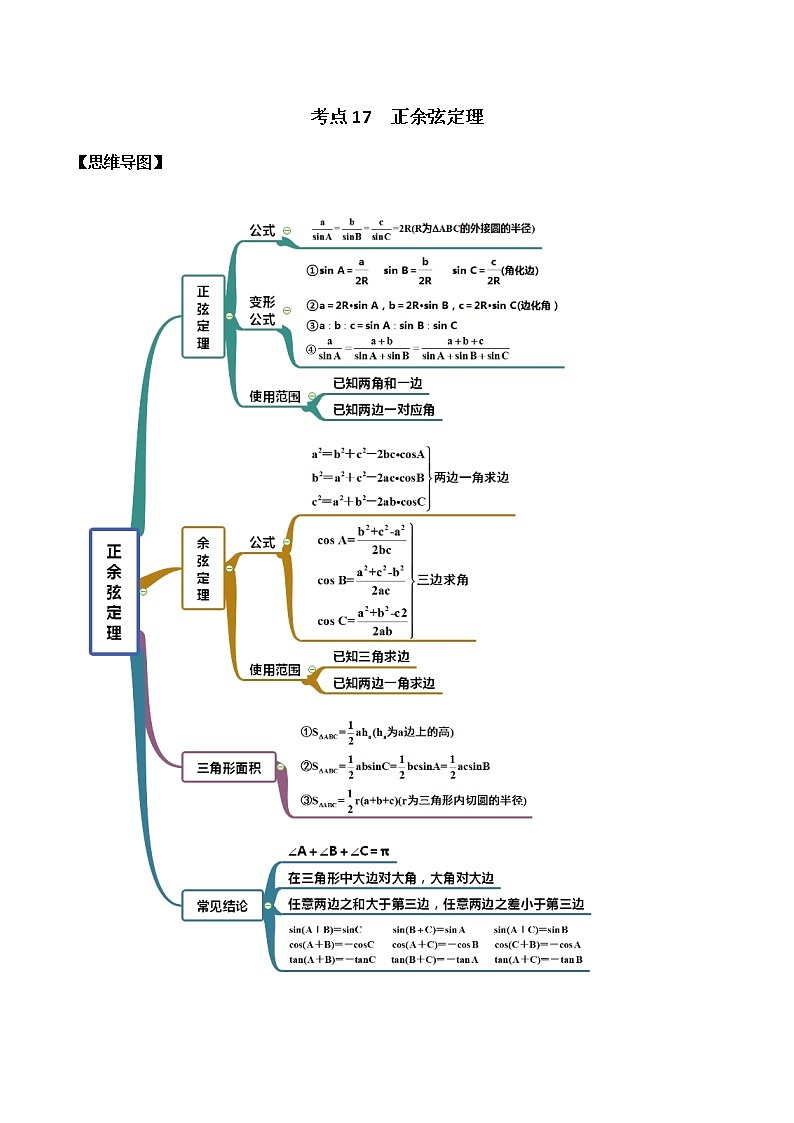
【思维导图】

【常见考法】

考法一：正余弦定理选择

1．中，角所对的边分别为．若，则边           。

【答案】4

【解析】，即，解得或（舍去）．

2．在中，，，，则的外接圆面积为      。

【答案】

【解析】因为在中，，，所以，

又，设三角形外接圆半径为，则，因此的外接圆面积为.

3．在△ABC中，A＝60°，a＝，则等于     。

【答案】

【解析】由正弦定理，==

∴a=sinA，b=sinB，c=sinC则==

4.在△ABC中，cos ＝，BC＝1，AC＝5，则AB＝          。

【答案】4　

【解析】因为cos C＝2cos2－1＝2×2－1＝－，所以c2＝a2＋b2－2abcos C＝1＋25－2×1×5×＝32，∴c＝AB＝4。

5.在△ABC中，BC＝2，AB＝4，cos C＝－，则AC的值为(　　 )

【答案】3　　

【解析】△ABC中，a＝BC＝2，c＝AB＝4，cos C＝－，∴c2＝a2＋b2－2abcos C，即16＝4＋b2－4b×，化简得b2＋b－12＝0，解得b＝3或b＝－4(不合题意，舍去)，∴b＝AC＝3.

考法二：边角互换

1．在△ABC中，若a＝2bsinA，则角B等于               。

【答案】30°或150°

【解析】由正弦定理有,因为.因为,故.即,又,故B等于30°或150°.

2．已知的三个内角所对边长分别是，若，则角的大小为     。

【答案】

【解析】由正弦定理得，化简得，故.

3．在中,,则角的大小为       。

【答案】

【解析】根据正弦定理得到：，根据余弦定理得到.

故.

4．在中，内角的对边长分别为，已知，且，则_________．

【答案】4

【解析】∵

∴根据正弦定理与余弦定理可得：，即

∵∴∵∴故答案为4

5．在中，分别是角的对边,若,且，则的值为   。

【答案】2

【解析】在中，因为,且，

由正弦定理得，

因为，则，

所以，即，解得，

由余弦定理得，

即，解得．

6．已知的三个内角所对边长分别是，若，则角的大小为  ．

【答案】

【解析】由正弦定理得，化简得，故.

考法三：三角形面积

1．在中，内角对应的边分别为，已知，，且，则的面积为     。

【答案】

【解析】因为，，所以由正弦定理得

即，得因为，所以所以

所以面积

2．在中，角，，的对边分别为，，，若，，且，则的面积为______.

【答案】2

【解析】由余弦定理得，即，解得，

∴，∴，

故.故答案为：2

3．在△ABC中，内角A，B，C的对边分别是a，b，c，若cos B＝，＝2，且S△ABC＝， 则b的值为   。

【答案】3

【解析】根据正弦定理可得,.

在中,,.

,,.

,.

4．在△中，，，，且△的面积为，则=_______

【答案】

【解析】，，∵，∴，∴．

考点四：三角形形状判断

1．在中，已知，则该的形状为             。

【答案】等腰或直角三角形

【解析】化为，

，，

至少有一个是锐角，，

或，或,所以是等腰三角形或直角三角形.

2．在中，角A，B，C的对边分别为a，b，c，满足且三边a，b，c成等比数列，则这个三角形的形状是    。

【答案】等边三角形

【解析】三边a，b，c成等比数列，即，根据余弦定理，即，.故为等边三角形.

3．已知三内角、、的对边分别是、、，若，且，则的形状为          。

【答案】等腰直角三角形

【解析】由正弦定理得，即，

所以，.又，由余弦定理得,所以,所以，所以为等腰直角三角形.

4．如果把直角三角形的三边都增加同样的长度，则这个新的三角形的形状为      。

【答案】锐角三角形

【解析】不妨设为直角三角形，，则，设三边增加的长度为，则新三角形的三边长度分别为，则，而，所以，因此新三角形为锐角三角形.

5．对于，有如下命题：

若，则一定为等腰三角形．

若，则一定为等腰三角形．

若，则一定为钝角三角形．

若，则一定为锐角三角形．

则其中正确命题的序号是______ 把所有正确的命题序号都填上

【答案】，，

【解析】或，为等腰或直角三角形正确；

由可得由正弦定理可得

再由余弦定理可得，为钝角，命题正确

全为锐角，命题正确

故其中正确命题的序号是，，

考点五：三角形个数

1．已知中，，，若仅有一解，则     。

【答案】

【解析】由题中已知中，，，则角所对的高线长可表示为，因为三角形形状唯一，所以三角形为直角三角形或钝角三角形，则 或， 所以 或

2．在三角形中,根据下列条件解三角形,其中有两个解的是     。

A．,, B．,,

C．,, D．,,

【答案】D

【解析】A已知两角一边，三角形确定的，只有一解，B已知两边及夹角用余弦定理，只有一解，C中已知两边及一边对角，但已知的是大边所对的角，小边所对角只能是锐角，不可能有两解，D中，，有两解．故选：D.

3．在中，角A，B，C的对边分别为a，b，c，则满足，，的三角形解的个数是______.

【答案】2

【解析】根据正弦定理得到：，故，.

故满足条件的三角形共有个.故答案为：.

4．若满足条件的三角形ABC有两个，那么a的取值范围是       。

【答案】

【解析】根据正弦定理可知 ，代入可求得 因为，所以

若满足有两个三角形ABC则 所以

考点六：取值范围

1．在中，角所对的边分别为，，的平分线交于点D，且，则的最小值为________．

【答案】9

【解析】由题意可知，,由角平分线性质和三角形面积公式得，化简得，因此

2．中，内角，，所对的边分别为，，.已知，且，则面积的最大值是__________．

【答案】

【解析】由及正弦定理得，

，即，

又，于是可得，即，.

在中，由余弦定理得，即，

又因为，，

由此可得，当且仅当时等号成立，

面积，故面积最大值为.故答案为

3．在锐角中，，，分别为三边，，所对的角，若，且满足关系式，则的取值范围是    。

【答案】

【解析】得，又，所以.

在锐角中，，由正弦定理得：

所以，

所以.

因为，所以，所以.

4．设，，分别为内角，，的对边.已知，则的取值范围为______.

【答案】

【解析】因为，所以，

所以，

即，又，所以，

则，因为，所以，

而，故.故答案为：．

5．在锐角三角形 ABC 中，已知 2sin2 A+ sin2B = 2sin2C，则的最小值为___．

【答案】

【解析】由正弦定理，得：，

如图，作BD⊥AC于D，设AD＝x，CD＝y，BD＝h，

因为，所以，，化简，得：

，解得：x＝3y

，，，

＝＝

＝＝，当且仅当时取得最小值.

故答案为：.

考法七：解析几何中运用

1．如图,在,已知点在边上,,,,,则的长为     。

【答案】

【解析】由题意，

∴，．

2．的两边长分别为1，，第三边上的中线长为1，则其外接圆的直径为          。

【答案】2

【解析】，设，

在中，，即，①

在中，同理可得，②

①+②得，为等边三角形，

，的外接圆直径为 .

3．在中，，则        。

【答案】

【解析】设

所以，

所以，

所以，

得

所以

4.如图，在△ABC中，点D在AC上，AB⊥BD，BC＝3，BD＝5，sin∠ABC＝，则CD的长为  。

【答案】4

【解析】利用余弦定理求解．因为sin∠ABC＝sin＝cos∠DBC＝，在△DBC中，由余弦定理可得CD2＝BD2＋BC2－2BD·BCcos∠DBC＝25＋27－2×5×3×＝16，所以CD＝4。

5.在△ABC中，∠ABC＝90°，AB＝4，BC＝3，点D在线段AC上．若∠BDC＝45°，则BD＝________，cos∠ABD＝________.

【答案】，

【解析】在ΔABD中，有：＝，而AB＝4，∠ADB＝，AC＝＝5，sin∠BAC＝＝，cos∠BAC＝＝，所以BD＝.cos∠ABD＝cos(∠BDC－∠BAC)＝coscos∠BAC＋sinsin∠BAC＝.

考点八：综合运用

1．在△ABC中,角A,B,C所对的边分别为，,,,则的值为     。

【答案】

【解析】因为，所以

.

2．在中，，向量 在上的投影的数量为，则  。

【答案】

【解析】∵向量 在上的投影的数量为，∴．①

∵，∴，∴．②

由①②得，∵为的内角，∴，∴．

在中，由余弦定理得

，∴．

3．设a，b，c分别是的内角A，B，C的对边，已知，设D是BC边的中点，且的面积为，则等于       。

【答案】2

【解析】∵，，

∴由正弦定理可得：，整理可得：b2+c2﹣a2=-bc，

∴由余弦定理可得：cosA=，∴由A∈（0，π），可得：A=，又的面积为，即,∴bc=4,又=-=-=-

===-bccosA=2.

4．要测量电视塔AB的高度，在C点测得塔顶的仰角是45°，在D点测得塔顶的仰角是30°，并测得水平面上的∠BCD=120°，CD=40m，则电视塔的高度是        。

【答案】40m

【解析】由题题意，设 则

在 中， ∴根据余弦定理，得 即：

整理得 解之得 或 （舍）即所求电视塔的高度为40米．
5．设，分别是双曲线的左、右焦点.若双曲线上存在一点，使得，且，则该双曲线的离心率是    。

【答案】

【解析】,分别是双曲线的左、右焦点,且双曲线上的点满足 所以,解得

因为,所以在三角形中由余弦定理可得

,代入可得

化简可得,即 所以

.