

考点45 算法与程序框图-备战2022年高考数学(理)一轮复习考点微专题学案
展开考点45 算法与程序框图
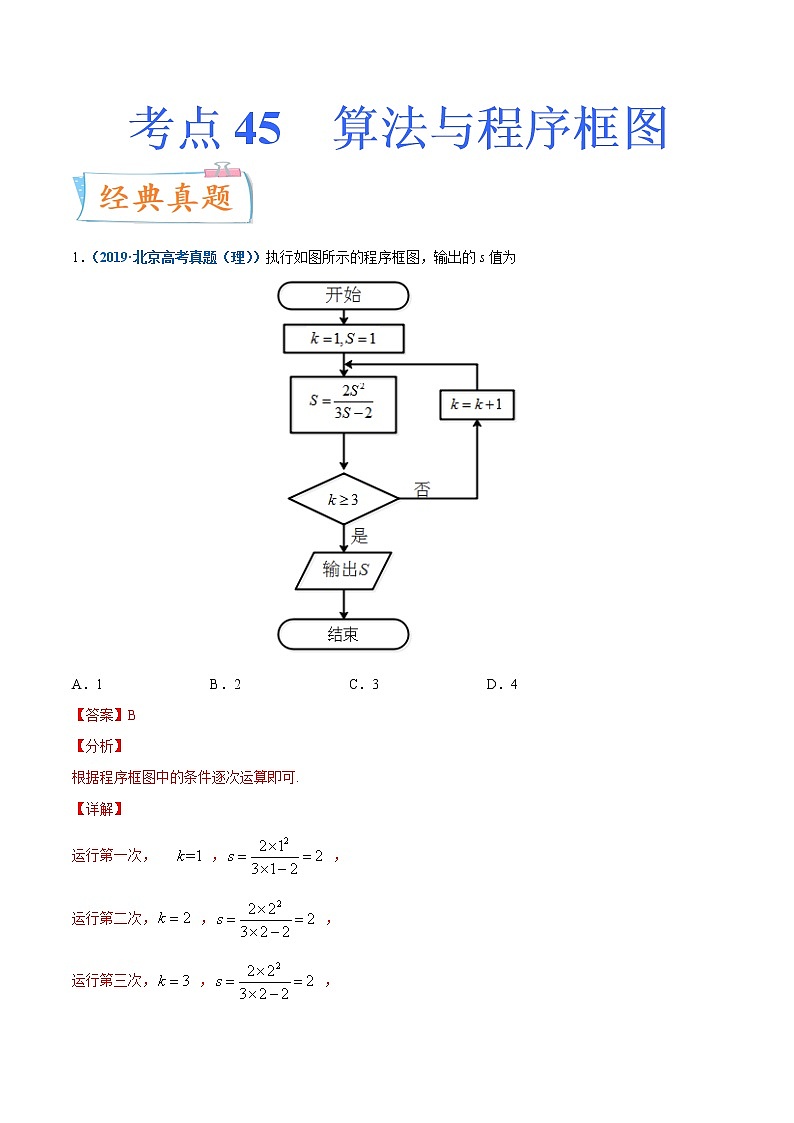
1.(2019·北京高考真题(理))执行如图所示的程序框图,输出的s值为
A.1 B.2 C.3 D.4
【答案】B
【分析】
根据程序框图中的条件逐次运算即可.
【详解】
运行第一次, , ,
运行第二次, , ,
运行第三次, , ,
结束循环,输出 ,故选B.
【点睛】
本题考查程序框图,属于容易题,注重基础知识、基本运算能力的考查.
1.一个共同点 一般只有一个入口也只能在一个出口输出,每一个基本逻辑结构的每一部分都有机会被执行到,而且结构内不能有死循环. 2.两种结构特点 (1)利用循环结构表示算法,一定要先确定是用当型循环结构,还是用直到型循环结构;当型循环结构的特点是先判断再循环,直到型循环结构的特点是先执行一次循环体,再判断. (2)循环结构中,当型循环又称“前测试型”循环,直到型循环又称“后测试型”循环. 3.三点提醒 (1)确定循环变量和初始值; (2)确定算法中反复执行的部分,即循环体; (3)确定循环的终止条件. |
一、算法的概念
1、算法概念:
在数学上,现代意义上的“算法”通常是指可以用计算机来解决的某一类问题是程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成.
2. 算法的特点:
(1)有限性:一个算法的步骤序列是有限的,必须在有限操作之后停止,不能是无限的.
(2)确定性:算法中的每一步应该是确定的并且能有效地执行且得到确定的结果,而不应当是模棱两可.
(3)顺序性与正确性:算法从初始步骤开始,分为若干明确的步骤,每一个步骤只能有一个确定的后继步骤,前一步是后一步的前提,只有执行完前一步才能进行下一步,并且每一步都准确无误,才能完成问题.
(4)不唯一性:求解某一个问题的解法不一定是唯一的,对于一个问题可以有不同的算法.
(5)普遍性:很多具体的问题,都可以设计合理的算法去解决,如心算、计算器计算都要经过有限、事先设计好的步骤加以解决.
二、程序框图
(一)程序构图的概念:程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形。
一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明。
(二)构成程序框的图形符号及其作用
程序框 | 名称 | 功能 |
| 起止框 | 表示一个算法的起始和结束,是任何流程图不可少的。 |
| 输入、输出框 | 表示一个算法输入和输出的信息,可用在算法中任何需要输入、输出的位置。 |
| 处理框 | 赋值、计算,算法中处理数据需要的算式、公式等分别写在不同的用以处理数据的处理框内。 |
| 判断框 | 判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不成立时标明“否”或“N”。 |
学习这部分知识的时候,要掌握各个图形的形状、作用及使用规则,画程序框图的规则如下:
1、使用标准的图形符号。
2、框图一般按从上到下、从左到右的方向画。
3、除判断框外,大多数流程图符号只有一个进入点和一个退出点。判断框具有超过一个退出点的唯一符号。
4、判断框分两大类,一类判断框“是”与“否”两分支的判断,而且有且仅有两个结果;另一类是多分支判断,有几种不同的结果。
5、在图形符号内描述的语言要非常简练清楚。
(三)算法的三种基本逻辑结构:顺序结构、条件结构、循环结构。
1、顺序结构
顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的,它是由若干个依次执行的处理步骤组成的,它是任何一个算法都离不开的一种基本算法结构。
顺序结构在程序框图中的体现就是用流程线将程序框自上而
下地连接起来,按顺序执行算法步骤。如在示意图中,A框和B
框是依次执行的,只有在执行完A框指定的操作后,才能接着执
行B框所指定的操作。
2、条件结构
条件结构是指在算法中通过对条件的判断根据条件是否成立而选择不同流向的算法结构。
条件P是否成立而选择执行A框或B框。无论P条件是否成立,只能执行A框或B框之一,不可能同时执行A框和B框,也不可能A框、B框都不执行。一个判断结构可以有多个判断框。
3、循环结构
在一些算法中,经常会出现从某处开始,按照一定条件,反复执行某一处理步骤的情况,这就是循环结构,反复执行的处理步骤为循环体,显然,循环结构中一定包含条件结构。循环结构又称重复结构,循环结构可细分为两类:
(1)、一类是当型循环结构,如下左图所示,它的功能是当给定的条件P成立时,执行A框,A框执行完毕后,再判断条件P是否成立,如果仍然成立,再执行A框,如此反复执行A框,直到某一次条件P不成立为止,此时不再执行A框,离开循环结构。
(2)、另一类是直到型循环结构,如下右图所示,它的功能是先执行,然后判断给定的条件P是否成立,如果P仍然不成立,则继续执行A框,直到某一次给定的条件P成立为止,此时不再执行A框,离开循环结构。
当型循环结构 直到型循环结构
注意:1.循环结构要在某个条件下终止循环,这就需要条件结构来判断。因此,循环结构中一定包含条件结构,但不允许“死循环”。
2在循环结构中都有一个计数变量和累加变量。计数变量用于记录循环次数,累加变量用于输出结果。计数变量和累加变量一般是同步执行的,累加一次,计数一次。
1.(2021·四川省绵阳南山中学高三其他模拟(理))程序框图如下图所示,若该程序运行的结果1320,则判断框中应填入( )
A. B. C. D.
2.(2021·全国高三其他模拟(理))如框图,当,时,输出的结果为,则等于( )
A.7 B.8 C.12 D.14
3.(2021·正阳县高级中学高三其他模拟(理))运行如图所示的程序框图,若输出的,则判断框中可以填( )
A.? B.? C.? D.?
4.(2021·陕西西安市·西安中学高三其他模拟(理))某算法框图如图所示,若该程序运行后输出的值是,则整数的值为( )
A.6 B.7 C.8 D.9
5.(2021·全国高三专题练习(理))执行如图所示的程序框图,若输出结果为,则中可填( )
A. B.
C. D.
6.(2021·贵州高三二模(理))已知,执行如图所示的程序框图,则输出的值为( )
A.3 B.
C. D.4
7.(2021·新疆阿勒泰地区·布尔津县高级中学高三三模(理))阅读如图所示的程序框图,若输入的,则该算法的功能是( )
A.计算数列的前8项和 B.计算数列的前7项和
C.计算数列的前8项和 D.计算数列的前7项和
8.(2021·全国高三其他模拟(理))如图所示的程序框图的功能是求函数的函数值,若,则不等式的解集为( )
A. B.
C. D.
9.(2021·江西上饶市·高三其他模拟(理))执行如图所示的程序框图,若输入,则输出S=( )
A.-1 B.
C.1 D.2
10.(2019·湖北高三开学考试(理))执行如图所示的程序框图,则输出的结果是( ).
A.7 B.8 C.9 D.10
11.(2021·全国高三专题练习(理))执行如图所示的程序框图,若输出的,则输入的( ).
A.
B.
C.
D.
12.(2021·全国高三月考(理))执行如图所示的程序框图,输出的值为( )
A.2048 B.1024 C.2046 D.4094
13.(2021·江西上饶市·(理))阅读如图的算法框图,输出结果的值为( )
A.0 B. C.2 D.
14.(2021·江西南昌市·高三一模(理))如图,将框图输出的看成输入的的函数,得到函数,则的图象( )
A.关于直线对称 B.关于直线对称
C.关于轴对称 D.关于点对称
15.(2012·陕西高考真题(理))右图是用模拟方法估计圆周率的程序框图,表示估计结果,则图中空白框内应填入( )
A.
B.
C.
D.
16.(2013·浙江高考真题(理))某程序框图如图所示,若该程序运行后输出的值是,则( )
A.a=4 B.a=5 C.a=6 D.a=7
17.(2011·陕西高考真题(理))右图中,为某次考试三个评阅人对同一道题的独立评分,为该题的最终得分,当,时等于
A. B. C. D.
18.(2021·江苏高考真题)下图是一个程序框图,执行该程序框图,则输出的n值是___________.
19.(2013·山东高考真题(理))执行如图的程序框图,若输入的的值为,则输入的的值_____.
20.(2015·安徽高考真题(理))执行如图所示的程序框图(算法流程图),输出的n为________.
1.C
【分析】
按照程序框图的流程写出前几次循环的结果,判断出当为何值时输出,得到判断框中的条件.
【详解】
经过第一次循环得到,不输出,即的值不满足判断框的条件
经过第二次循环得到,不输出,即的值不满足判断框的条件
经过第三次循环得到,输出,即的值满足判断框的条件
故判断框中的条件是:?.
故选:.
2.C
【分析】
根据程序框图,判断输出的,从而可得答案.
【详解】
因为,,
所以,
所以输出的,
所以,
故选:C.
3.C
【分析】
通过进行循环的简单计算,找出的基本规律,当第1011次循环时,符合题设条件,此时,判断选项即可
【详解】
模拟运行该程序,第1次循环,,,第2次循环,,,第3次循环,,,…,第1011次循环,,,观察可知,仅C正确,
故选:C.
4.A
【分析】
根据程序框图,逐步只需,直到能输出为止,即可判断的值.
【详解】
执行框图如下:
初始值,,此时,需要执行循环体,
计算,,需要继续执行循环体;
计算,,需要继续执行循环体;
计算,,需要继续执行循环体;
计算,,需要继续执行循环体;
计算,,需要继续执行循环体;
计算,,此时需要输出;
因此,
故选:A.
5.B
【分析】
计算可得,由程序框图可知其功能为计算数列的前项和,由裂项相消法可确定的取值,由此判断出判断框所需条件.
【详解】
,
由程序框图知:表示数列的前项和,
则,
又输出结果为,,解得:,
则当时,不满足判断框条件;当时,满足判断框条件,输出结果,则满足条件的条件为:.
故选:B.
【点睛】
方法点睛:本题以程序框图为载体考查了裂项相消法求解数列的前项和的问题,裂项相消法适用于通项公式为形式的数列,即,进而前后相消求得结果.
6.A
【分析】
先计算定积分得,再根据程序框图可得,进而分母有理化求和即可得答案.
【详解】
因为,
所以执行框图可得
.
故选:A
【点睛】
本题考查程序框图,定积分,数列求和,考查运算求解能力,是中档题.本题解题的关键在于根据程序框图得,进而根据求和即可.
7.C
【分析】
根据程序框图,依次计算出i取1,2,3,…,8时的S值,再由各选项的条件判断得解.
【详解】
S=0,i=1;
判断i>8不成立,执行S=1+2×0=1,i=1+1=2;
判断i>8不成立,执行S=1+2×1=1+2,i=2+1=3;
判断i>8不成立,执行S=1+2×(1+2)=1+2+22,i=3+1=4;
判断i>8不成立,执行S=1+2×(1+2+22)=1+2+22+23,i=4+1=5;
判断i>8不成立,执行S=1+2×(1+2+22+23)=1+2+22+23+24,i=5+1=6;
判断i>8不成立,执行S=1+2×(1+2+22+23+24)=1+2+22+23+24+25,i=6+1=7;
判断i>8不成立,执行S=1+2×(1+2+22+23+24+25)=1+2+22+23+24+25+26,i=7+1=8;
判断i>8不成立,执行S=1+2×(1+2+22+23+24+25+26)=1+2+22+23+24+25+26+27,i=8+1=9;
判断i>8成立,输出S=1+2+22+23+24+25+26+27,
算法结束.
所以输出的S是数列的前8项和.
故选:C
【点睛】
关键点睛:程序框图循环结构的功能判断,关键是能够准确求解输出的结果,从而可根据结果判断出功能.
8.A
【分析】
根据流程图写出函数的解析式,因为是分段函数,需要对自变量进行讨论,然后比较与的大小,从而解出x的取值范围.
【详解】
由题中的程序框图可得
①当时,,不满足,舍去;
②当时,,不满足,舍去;
③当时,,可得,
所以不等式的解集为.
故选:A.
【点睛】
关键点点睛:求得分段函数解析式,对自变量分类讨论,解不等式,求得解集.
9.B
【分析】
根据题意,模拟程序框图的运行过程,即可得出输出的S的值.
【详解】
模拟程序框图的运行过程:
S | i | 判断条件 |
2 | 1 | 是 |
2 | 是 | |
3 | 是 | |
2 | 4 | 是 |
5 | 是 | |
6 | 是 | |
2 | 7 | 是 |
8 | 是 | |
9 | 是 | |
2 | 10 | 是 |
11 | 否 |
时,,选“是”,继续循环,
时,,选“否”,输出
故选:B.
【点睛】
框图类问题的解题策略:
(1) 模拟程序框图的运行过程;
(2)循环结构的题目要注意循环终止的条件.
10.B
【分析】
根据题意,模拟程序框图的运行过程,即可得出输出的S的值.
【详解】
模拟程序框图的运行过程:
S | n | 判断条件 |
0 | 1 | 否 |
2 | 否 | |
3 | 否 | |
4 | 否 | |
5 | 否 | |
6 | 否 | |
7 | 否 | |
8 | 是 |
时,,此时,选“否”,
时,,此时,选“是”,输出n
故选:B.
【点睛】
框图类问题的解题策略:
(1) 模拟程序框图的运行过程;
(2)循环结构的题目要注意循环终止的条件.
11.B
【分析】
根据程序框图可知,当时循环结束,计算出此时的表达式,根据输出的计算出输入的值.
【详解】
,,,否,
,,,否,
,,,否,
,,,是,退出循环,
则,.
故选:B.
【点睛】
本题考查根据算法框图的输出结果判断输入框中数据的大小,解答的本题的关键是要读懂程序框图的功能,根据循环的控制条件确定好循环的起止,注意在赋值语句“”中,分母的值为最近一次赋值的结果,然后代入重新赋值得到.
12.C
【分析】
按照程序框图逐次写出循环结果,直到结束循环即可得值.
【详解】
,,
运行第1次,,
运行第2次,,
运行第9次,,
运行第10次,,,结束循环
故输出的值2046
故选:C.
【点睛】
关键点点睛:本题主要考查的是程序框图,按照程序框图判断何时结束循环是解题的关键,是基础题.
13.C
【分析】
由程序框图知,该程序的功能是计算,而的周期为,且一个周期内和为0,进一步可求得结果.
【详解】
由程序框图知,该程序的功能是计算,
由函数的周期性,知该等式中每连续个的值的和等于,
而,所以这个值等于前3个的和,
即.
故选:C.
【点睛】
易错点点睛:本题主要考查程序框图的循环结构流程图,属于中档题. 解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支结构还是循环结构;(3) 注意区分当型循环结构和直到型循环结构;(4) 处理循环结构的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,(6)在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可.
14.D
【分析】
由框图得到分段函数,再利用分段函数性质验证选项得解.
【详解】
由框图得到分段函数 画出图象如下
则由图得D正确
故选D
15.D
【解析】
试题分析:由题意以及程序框图可知,用模拟方法估计圆周率π的程序框图,M是圆周内的点的次数,当i大于1000时,圆周内的点的次数为4M,总试验次数为1000,所以要求的概率,所以空白框内应填入的表达式是
考点:程序框图
16.A
【详解】
由已知可得该程序的功能是
计算并输出S=1++…+=1+1﹣=2﹣.
若该程序运行后输出的值是,则 2﹣=.
∴a=4,
故选A.
17.C
【详解】
先读懂右图的逻辑顺序,然后进行计算判断,其中判断条件是否成立是解答本题的关键.
,,不成立,即为“否”,所以再输入;由绝对值的意义(一个点到另一个点的距离)和不等式知,点到点的距离小于点到的距离,所以当时,成立,即为“是”,此时,所以,即,解得,不合题意;当时,不成立,即为“否”,此时,所以,即,解得,符合题意,故选C.
18.2
【分析】
程序框图中的循环结构,一般需重复计算,根据判断框中的条件,确定何时终止循环,输出结果.
【详解】
初始值:,
当时,,进入循环;
当时,,进入循环;
当时,,终止循环,输出的值为.
故答案为:2.
19.
【详解】
根据运行顺序计算出的值,当≤ε时输出n的值,结束程序.
由程序框图可知:
第一次运行:F1=1+2=3,F0=3-1=2,n=1+1=2,=>ε,不满足要求,继续运行;
第二次运行:F1=2+3=5,F0=5-2=3,n=2+1=3,==0.2<ε,满足条件.
结束运行,输出n=3.
20.4
【解析】
由题意,程序框图循环如下:①;②;③;④,此时,所以输出.
考点:1.程序框图的应用.
考点45 直线与圆、圆与圆的位置关系(考点详解)-备战2022年新高考数学一轮复习考点微专题学案: 这是一份考点45 直线与圆、圆与圆的位置关系(考点详解)-备战2022年新高考数学一轮复习考点微专题学案,共7页。学案主要包含了直线与圆的位置关系;,圆与圆的位置关系;,直线与圆的综合问题等内容,欢迎下载使用。
考点30 椭圆-备战2022年高考数学(理)一轮复习考点微专题学案: 这是一份考点30 椭圆-备战2022年高考数学(理)一轮复习考点微专题学案,共23页。学案主要包含了考点定位,技巧点晴等内容,欢迎下载使用。
考点29 圆的方程-备战2022年高考数学(理)一轮复习考点微专题学案: 这是一份考点29 圆的方程-备战2022年高考数学(理)一轮复习考点微专题学案,共19页。学案主要包含了名师点睛等内容,欢迎下载使用。












