华师大版九年级上册第24章 解直角三角形综合与测试复习课件ppt

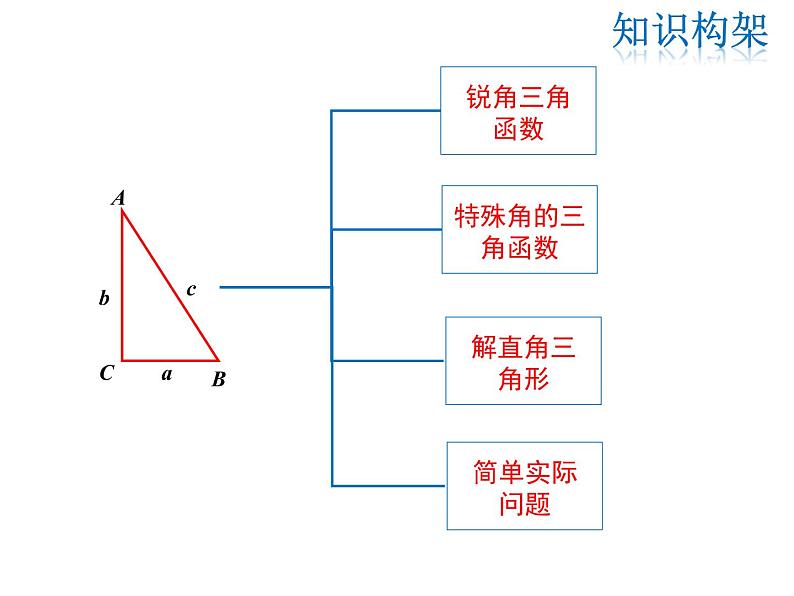
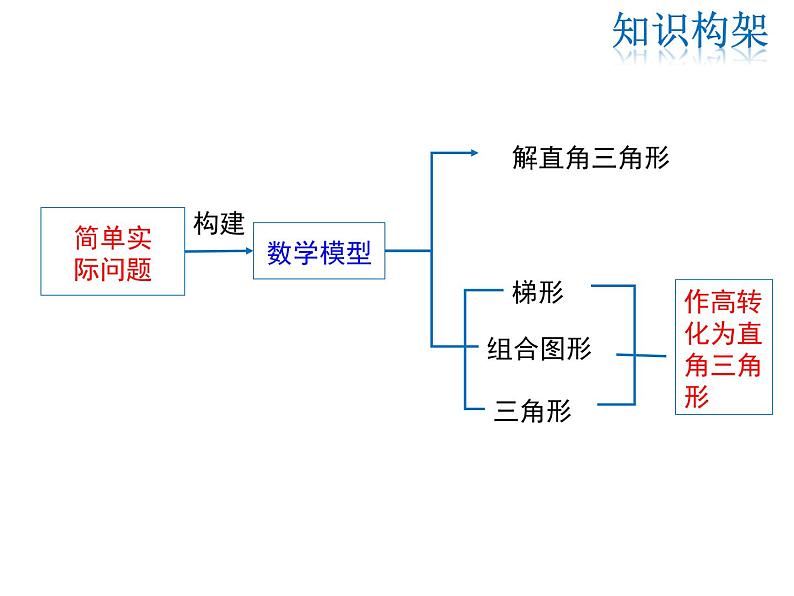
这是一份华师大版九年级上册第24章 解直角三角形综合与测试复习课件ppt，共21页。PPT课件主要包含了锐角三角函数，特殊角的三角函数，解直角三角形，简单实际问题，知识构架，两边之比，a2+b2c2，三角函数关系式，计算器，由锐角求三角函数值等内容，欢迎下载使用。
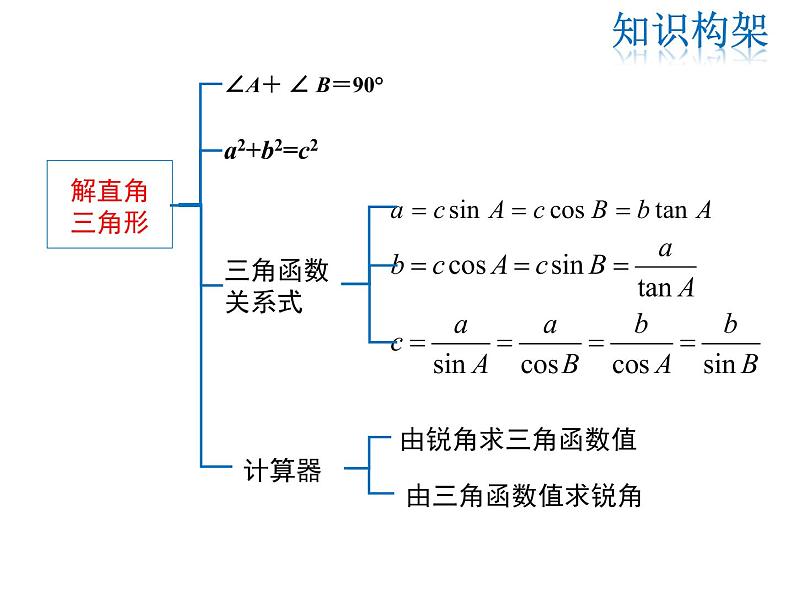
∠A＋ ∠ B＝90°
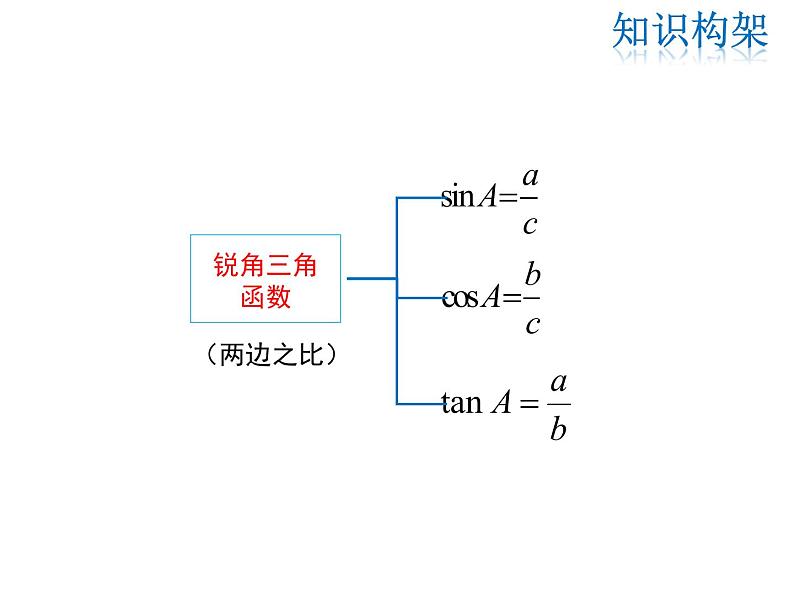
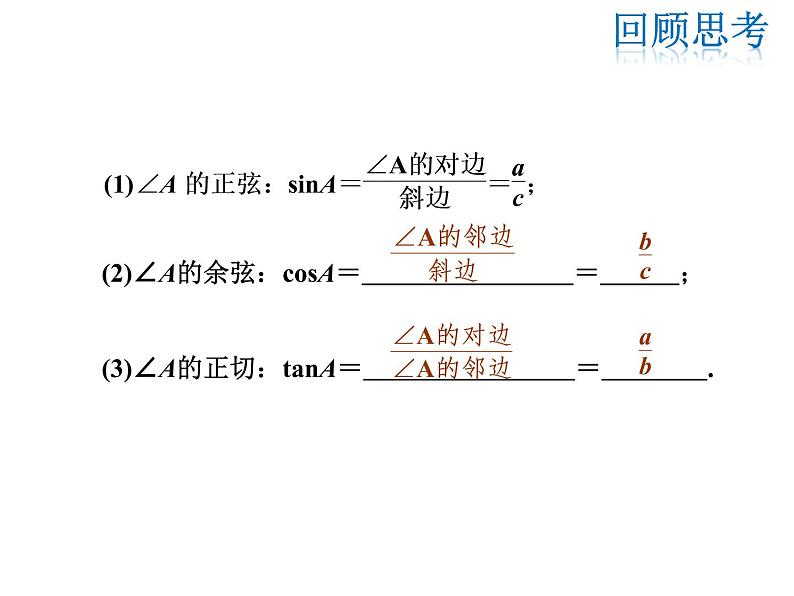
(2)∠A的余弦：csA＝　　　　　　　　＝　　　；(3)∠A的正切：tanA＝　　　　　　　　＝　　　　.
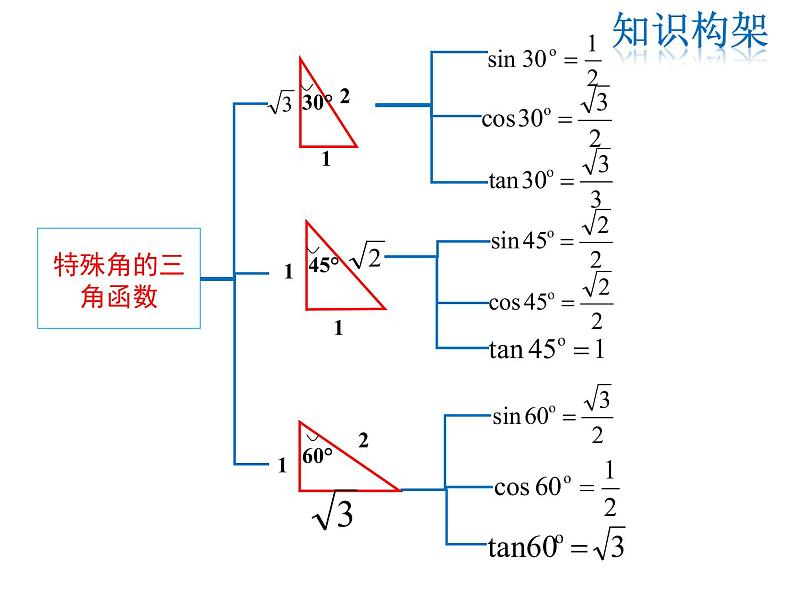
易错点： 忽视用边的比表示锐角的正弦、余弦和正切的前提是在直角三角形中．2．30°、45°、60°角的三角函数值sin30°＝　　　，sin45°＝　　　，sin60°＝　　　；cs30°＝　　　，cs45°＝　　　，cs60°＝　　　；tan30°＝　　　，tan45°＝　　　，tan60°＝　　　.3．解直角三角形的依据(1)在Rt△ABC中，∠C＝90°，a、b、c分别是∠A、∠B、∠C的对边．
三边关系：　 　；三角关系：　 ；边角关系：sinA＝csB＝　　　，csA＝sinB＝ ，tanA＝　　　　　　，tanB＝　　　　　　.(2)直角三角形可解的条件和解法条件：解直角三角形时知道其中的2个元素(至少有一个是边)，就可以求出其余的3个未知元素．
解法：①一边一锐角，先由锐角关系求出另一锐角；知斜边，再用正弦(或余弦)求另两边；知直角边用正切求另一直角边，再用正弦或勾股定理求斜边．②知两边：先用勾股定理求另一边，再用边角关系求锐角．③斜三角形问题可通过添加适当的辅助线转化为解直角三角形问题．
1.如图，在△ABC中，∠C＝90°，点D在BC上，BD＝4，AD＝BC，cs∠ADC= ，求：（1）DC的长；（2）sinB的值．
分析：题中给出了两个直角三角形，DC和sinB可分别在Rt△ACD和Rt△ ABC中求得，由AD＝BC，图中CD＝BC－BD，由此可列方程求出CD．
解：（1）设CD＝x，在Rt△ACD中，cs∠ADC= ,
(2) BC=BD+CD=4+6=10=AD.
解析： 要求△ABC的周长，先通过解Rt△ADC求出CD和AD的长，然后根据勾股定理求出AB的长．
3.如图所示，电视塔高AB为610米，远处有一栋大楼，某人在楼底C处测得塔顶B的仰角为45°，在楼顶D处测得塔顶B的仰角为39°.(1)求大楼与电视塔之间的距离AC；(2)求大楼的高度CD(精确到1米)．
解析： (1)利用△ABC是等腰直角三角形易得AC的长；(2)在Rt△BDE中，运用直角三角形的边角关系即可求出BE的长，用AB的长减去BE的长度即可．
解：(1)由题意，得∠ACB＝45°，∠A＝90°，∴△ABC是等腰直角三角形，∴AC＝AB＝610(米)．(2)DE＝AC＝610.在Rt△BDE中，tan∠BDE＝ ，∴BE＝DE·tan 39°.∵CD＝AE，∴CD＝AB－DE·tan 39°＝610- 610×tan39°≈116(米)．即大楼的高度CD约为116米．
解应用题时，先要将实际问题转化为数学问题，找出直角三角形并寻找联系已知条件和未知量的桥梁，从而利用解直角三角形的知识得到数学问题的答案，最后得到符合实际情况的答案．
解直角三角形的一般思路是：有斜(斜边)用弦(正弦、余弦)，无斜用切(正切)，宁乘勿除，取原避中．对于较复杂的图形，要善于将其分解成简单的图形，并借助桥梁(相等的边、公共边、相等的角等)的作用将两个图形有机地联系在一起，从而达到解题的目的．