专题8.61抛物线及其性质（一）（解析版）教案

这是一份专题8.61抛物线及其性质（一）（解析版）教案，共10页。
1.理解抛物线的定义及其标准方程；
2.理解抛物线的基本性质；
3.会解焦点弦和中点弦有关的简单问题。
教学过程
（一）必备知识：
1．抛物线的定义
平面内与一个定点F和一条定直线l(F ∉______)距离相等的点的轨迹叫做抛物线．
点F叫做抛物线的________，直线l叫做抛物线的________．
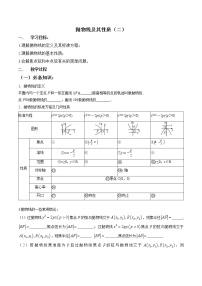
2．抛物线的标准方程及几何性质
自查自纠：
1．l 焦点 准线 2．①eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(p,2)，0)) ③eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(p,2))) ⑥x＝eq \f(p,2) ⑧y＝eq \f(p,2)
⑩x≤0，y∈R ⑪y≥0，x∈R ⑬x轴 ⑯e＝1⑰向右 ⑳向下
（二）题组训练：
题组一：
例1．抛物线的准线方程是（ ）
A. B. C. D.
【答案】D、
【详解】抛物线方程可化为，焦点,所以准线方程是，故选D.
例2.若坐标原点到抛物线的准线的距离为2，则（ ）
A．8 B． C． D．
【答案】D
【详解】将抛物线化为标准方程得，所以.
例3.如图，正方形和正方形的边长分别为a,b(a0),则焦点坐标为（），准线方程为x=,
课外作业：
1．设抛物线的顶点在原点，准线方程为x=﹣2，则抛物线的方程是（ ）
A．y2=﹣8xB．y2=8xC．y2=﹣4xD．y2=4x
【答案】B
【详解】∵准线方程为x=﹣2∴=2∴p=4∴抛物线的方程为y2=8x故选B
2．抛物线的焦点坐标是（ ）
A． B． C． D．
【答案】A
【详解】焦点，故选 A．
3．抛物线的焦点坐标是（ ）
A． B． C． D．
【答案】A
【详解】，可知焦点坐标为.
4．抛物线的焦点到直线的距离是（ ）
A． B． C． D．
【答案】C
【详解】焦点焦点到直线的距离是，故选C．
5．若抛物线y2=2px（p>0）的焦点是椭圆的一个焦点，则p=（ ）
A．2 B．3 C．4 D．8
【答案】D
【详解】因为抛物线的焦点是椭圆的一个焦点，所以，解得，故选D．
6．已知抛物线y2=2px(p>0)的准线经过点(-1,1)，则抛物线焦点坐标为（ ）
A．(-1,0) B．(1,0) C．(0,-1) D．(0,1)
【答案】B
【详解】由抛物线y2=2px(p>0)得准线x=-p2，因为准线经过点(-1,1)，所以p=2，
所以抛物线焦点坐标为(1,0)，故答案选B
7．以抛物线C的顶点为圆心的圆交C于A、B两点，交C的准线于D、E两点.已知|AB|=，|DE|=，则C的焦点到准线的距离为 ( )
A．8 B．6 C．4 D．2
【答案】C
【详解】如图，设抛物线方程为，交轴于点，则，即点纵坐标为，则点横坐标为，即，由勾股定理知，，即，解得，即的焦点到准线的距离为4，故选B.
培优题组：
1.在平面直角坐标系中，分别是轴和轴上的动点，若以为直径的圆与直线相切，则圆面积的最小值为（ ）
A．B．C．D．
【答案】A
【详解】设直线因为，表示点到直线的距离，所以圆心的轨迹为以为焦点，为准线的抛物线，圆的半径最小值为，圆面积的最小值为．故本题的正确选项为A.
2.若抛物线上有一条长为6的动弦，则的中点到轴的最短距离为（ ）
A． B． C．1 D．2
【答案】D
【详解】设，的中点到轴的距离为，如图所示，根据抛物线的定义，有，，故，最短距离为.
3.已知点，的焦点是，是上的动点，为使取得最小值，则点坐标为（ ）
A. B. C. D.
【答案】A
【详解】过作（为抛物线准线）于，则，所以，所以当点的纵坐标与点的纵坐标相同时，最小，此时的纵坐标为，把代入得，即当时，最小.故选A.
4.若点在上，点在上，则的最小值为（ ）
A. B. C. D.
【答案】B
【详解】设，圆的圆心，半径
，由二次函数性质可知的最小值为，所以的最小值为. 标准方程
y2＝2px(p＞0)
y2＝－2px(p＞0)
x2＝2py(p＞0)
x2＝－2py(p＞0)
图形
性质
焦点
①
②eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(p,2)，0))
③
④eq \b\lc\(\rc\)(\a\vs4\al\c1(0，－\f(p,2)))
准线
⑤x＝－eq \f(p,2)
⑥
⑦y＝－eq \f(p,2)
⑧
范围
⑨x≥0，y∈R
⑩
⑪
⑫y≤0，x∈R
对称轴
⑬
⑭y轴
顶点
⑮原点O(0，0)
离心率
⑯
开口
⑰
⑱向左
⑲向上
⑳