

一轮复习专题3.2 导数的应用(原卷版)教案
展开02导数的应用
一、必备知识
1.函数的单调性与导数
在某个区间(a,b)内,
如果f′(x)>0,那么函数y=f(x)在这个区间内____________;
如果f′(x)<0,那么函数y=f(x)在这个区间内____________;
如果在某个区间内恒有f′(x)=0,那么函数f(x)在这个区间上是________.
2.函数的极值与导数
(1)判断f(x0)是极大值,还是极小值的方法:
一般地,当f′(x0)=0时,
①如果在x0附近的左侧f′(x)>0,右侧f′(x)<0,那么f(x0)是极大值;
②如果在x0附近的左侧____________,右侧____________,那么f(x0)是极小值.
(2)求可导函数极值的步骤:
①求f′(x);
②求方程____________的根;
③检查f′(x)在上述根的左右对应函数值的符号.如果左正右负,那么f(x)在这个根处取得____________;如果左负右正,那么f(x)在这个根处取得____________.
3.函数的最值与导数
(1)在闭区间[a,b]上图象连续不断的函数f(x)在[a,b]上必有最大值与最小值.
(2)若函数f(x)在[a,b]上单调递增,则____________为函数在[a,b]上的最小值,____________为函数在[a,b]上的最大值;若函数f(x)在[a,b]上单调递减,则____________为函数在[a,b]上的最大值,____________为函数在[a,b]上的最小值.
(3)设函数f(x)在[a,b]上图象连续不断,在(a,b)内可导,求f(x)在[a,b]上的最大值和最小值的步骤如下:
①求f(x)在(a,b)内的极值;
②将f(x)的各极值与端点处的函数值______,______进行比较,其中最大的一个是________,最小的一个是________.
自查自纠:
1.单调递增 单调递减 常数函数
2.(1) ②f′(x)<0 f′(x)>0 (2) ②f′(x)=0 ③极大值 极小值
3.(2)f(a) f(b) f(a) f(b) (3) ②f(a) f(b) 最大值 最小值
二、考点题型:
题组一:
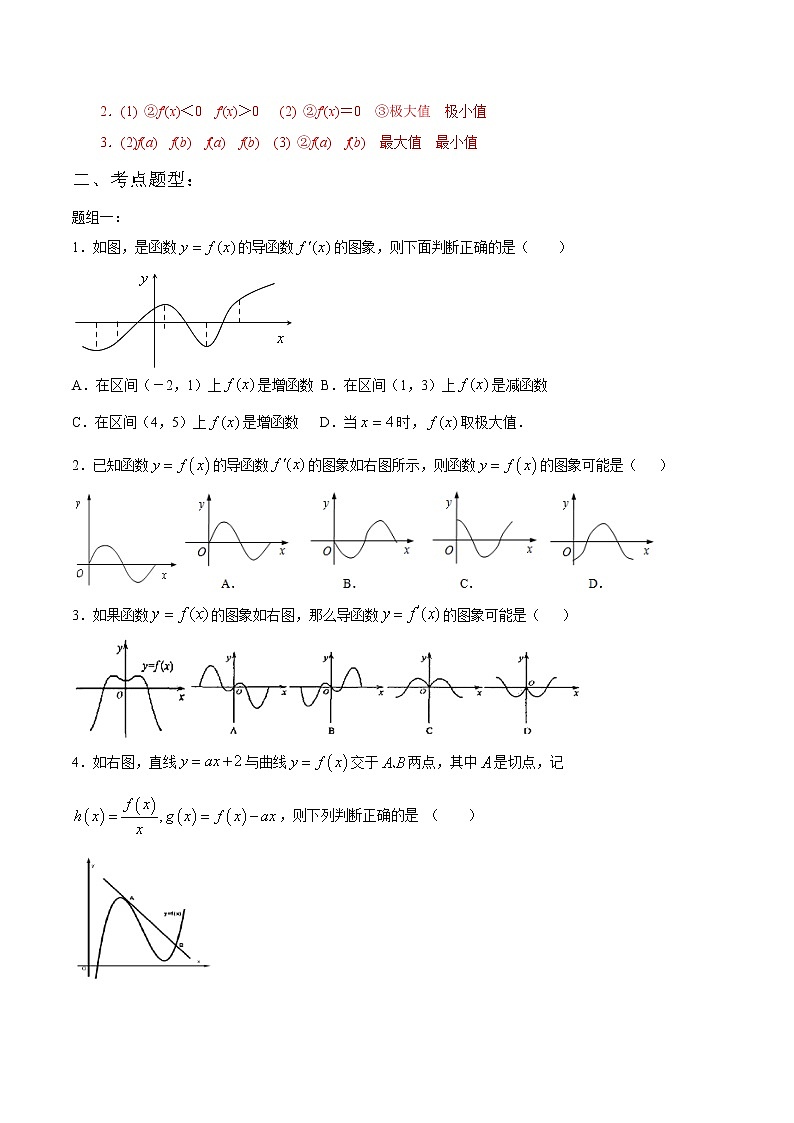
1.如图,是函数的导函数的图象,则下面判断正确的是( )
A.在区间(-2,1)上是增函数 B.在区间(1,3)上是减函数
C.在区间(4,5)上是增函数 D.当时,取极大值.
2.已知函数的导函数的图象如右图所示,则函数的图象可能是( )
3.如果函数的图象如右图,那么导函数的图象可能是( )
4.如右图,直线与曲线交于两点,其中是切点,记,则下列判断正确的是 ( )
A.只有一个极值点
B.有两个极值点,且极小值点小于极大值点
C.的极小值点小于极大值点,且极小值为-2
D.的极小值点大于极大值点,且极大值为2
课堂检测:
5.函数的图象如下图所示,则导函数的图象的大致形状是( )
A. B. C. D.
6.已知函数是上的可导函数, 的导数的图像如图,则下列结论正确的是( )
A.分别是极大值点和极小值点 B.分别是极大值点和极小值点
C.在区间上是增函数 D.在区间上是减函数
7.设函数在上可导,其导函数为,且函数在处取得极小值,则函数的图象可能是( )
A. B. C. D.
8.如图,已知直线与曲线相切于两点,则函数 有( )
A.个零点 B.个极值点
C.个极大值点 D.个极大值点
题组二:
9.函数的单调递减区间是( )
A. B. C. D.
10.函数的单调递增区间是( )
A. B. C. D.
11.函数单调增区间是________.
12.已知满足,则的单调递减区间是 .
课堂检测:
13.函数的单调减区间是( )
A. B. C. D.
14.已知定义在区间上的函数,则的单调递减区间是
15.设函数.若为奇函数,则函数的单调递减区间为_______.
题组三:
16.函数在上单调递增,则实数的取值范围是( )
A. B. C. D.
17.若函数在区间上单调递增,则实数的取值范围是( )
A. B. C. D.
18.若是上的减函数,则实数的取值范围是( )
A. B. C. D.
19.已知在区间上不单调,实数的取值范围是( )
A. B. C. D.
20.若函数在其定义域内的一个子区间内不是单调函数,则实数k的取值范围 ( )
A. B. C. D.
21.已知函数 (a>0),若f(x)为R上的单调函数,则实数a的取值范围是________.
22.已知函数f(x)=x3+ax2+x+1)在(-23,-13)内存在单调递减区间,则实数a的取值范围是( )
A.(0,3] B.(-∞,3] C.(3,+∞) D.(3,3)
24.若函数f(x)=x2-4ex-ax在R上存在单调递增区间,则实数a的取值范围为__________.
课堂检测:
23.若函数 在内单调递减,则实数的取值范围是( )
A. B. C. D.
24.若函数在区间上单调递减,则实数的取值范围是( )
A. B. C. D.
25.函数f(x)=ax-cosx,x∈ [,],若∀ x1,x2∈ [,],x1≠x2,,则实数a的取值范围是________.
26.函数f(x)=x2+ax-lnx在区间(1,2)上是单调函数,则实数a的取值范围是__________.
27.已知函数,则在(1,3)上不单调的一个充分不必要条件是( )
A. B. C. D.
28.已知函数f(x)=在上是减函数,则实数a的取值区间是___
29.若函数f(x)=12ax2+xlnx-x存在单调递增区间,则a的取值范围是( )
A.(-1e,1) B.(-1e,+∞) C.(-1,+∞) D.(-∞,1e)
题组四:
30.定义在上的函数满足,且,则不等式的解集为( )
A. B. C. D.
31.已知定义域为的函数,对任意的都有,且.当时,不等式的解集为( )
A. B. C. D.
32.定义在R上的函数满足:,,则不等式 的解集为( )
A.(0,+∞) B.(-∞,0)∪ ( 3,+ ∞) C.(-∞,0)∪ (0,+∞) D.(3,+ ∞)
33.已知函数对定义域内的任意都有,且当时,其导函数满足,若,则( )
A. B.
C. D.
34.定义在上的函数,是它的导函数,且恒有成立,则( )
A. B. C. D.
课堂检测:
35.已知函数(为自然对数的底数),若,则实数的取值范围是__________.
36.函数的定义域为,,对任意,,则的解集为( )
A. B. C. D.
37.已知的定义域为,的导函数,且满足,则不等式的解集是 ( )
A. B. C.(1,2) D.
38.函数在定义域上的导函数是,若,且当时,,设、、,则 ( )
A. B. C. D.
39 .已知定义在上的函数满足,且当时,成立,若,的大小关系是( )
A. B. C. D.
40.已知函数在上可导且满足,则下列一定成立的为( )
A. B. C. D.
41.已知为 上的可导函数,且,均有,则以下判断正确的是( )
A. B.
C. D.与大小无法确定
题组五:
42.函数f(x)=3x2+ln x-2x的极值点的个数是( )
A.0 B.1 C.2 D.无数个
43.函数在 处取得极小值.
44.设函数,则( )
A.为的极大值点 B.为的极小值点
C.为的极大值点 D.为的极小值点
45.已知函数,则的极大值点为( )
A. B. C. D.
46.已知函数,则( )
A.只有极大值 B.只有极小值 C.既有极大值也有极小值 D.既无极大值也无极小值
课堂检测:
47.函数的极值点的个数是( )
A.2 B.1 C.0 D.由a决定
48.已知函数在处取得极小值,则的极大值为( )
A. B. C. D.
49.函数,若函数的图象在处切线的斜率为,则的极大值是( )
A. B. C. D.
50.函数,为的一个极值点,且满足,则__
题组六:
51.已知函数在上可导,则“”是“为函数的极值”的( )
A.充分不必要条件 B.充要条件 C.必要不充分条件 D.既不充分也不必要条件
52.已知函数在处取得极小值,则________.
53.已知函数在x=2处取得极小值,则常数m的值为( )
A.2 B.8 C.2或8 D.以上答案都不对
54.已知函数在x=-1时有极值0,则=______ .
55.若y=alnx+bx2+x在x=1和x=2处有极值,则a、b的值分别为( )
A.a=1b=-13 B.a=16b=23 C.a=13b=-1 D.a=-23b=-16
56.已知函数f(x)=ax3+bx2+cx-17 (a,b,c∈R)的导函数为f'x,f'x≤0的解集为x-2≤x≤3,若f(x)的极小值等于-98,则a的值是( )
A.-8122 B.13 C.2 D.5
57.已知函数,若,但不是函数的极值点,则的值为_________.
课堂检测:
58.已知函数,当时函数的极值为,则 .
59.当是函数的极值点,则的值为( )
A.-2 B.3 C.-2或3 D.-3或2
60.若,且函数在处有极值,则的最大值等于( )
A.2 B.3 C.6 D. 9
61.设是函数的一个极值点,则____.
62.已知,函数和存在相同的极值点,则_______.
题组七:
63.连续函数f(x)的导函数为,若(x+1)·>0,则下列结论中正确的是 ( )
A.x=-1一定是函数f(x)的极大值点 B.x=-1一定是函数f(x)的极小值点
C.x=-1不是函数f(x)的极值点 D.x=-1不一定是函数f(x)的极值点
64.函数上既有极大值又有极小值,则的取值范围为( )
A. B. C. D.
65.对任意的x∈ R,函数不存在极值点的充要条件是( )
A. B.或 C.或 D.或
66.设,若函数有大于的极值点,则( )
A. B. C. D.
课堂检测:
67.已知函数存在极值,则实数m的取值范围为_ _________.
68.若函数存在极值,则实数的取值范围是( )
A. B. C. D.
69.函数有极值且极值大于0,则a的取值范围是( )
A. B. C. D.
题组八:
70.函数内有极小值,则( )
A. B. C. D.
71.若函数在内无极值,则实数的取值范围是( ).
A. B. C. D.
72.已知函数,在区间()上存在极值,则实数a的取值范围是( )
A.( 0,1) B.(,1) C.( ,1) D.( , 1)
课堂检测:
73.函数在内有极小值,则实数的取值范围是( )
A. B. C. D.
74.若在区间上有极值点,则实数的取值范围是( )
A. B. C. D.
75.设,若函数在区间有极值点,则取值范围为( )
A. B. C. D.
题组九:
76.已知函数的图象如图所示,则等于( )
A. B. C. D.
77.已知有两个不同的极值点,则的取值范围是( )
A. B. C. D.
78.已知函数有两个极值点,则直线的斜率的取值范围是( )
A. B. C. D.
课堂检测:
79.设函数的两个极值点分别为,若,,则的取值范围为( )
A. B. C. D.
80.已知函数的两个极值分别为 和 .若 和 分别在区间(-2,0)与(0,2)内,则 的取值范围为( )
A. B. C. D.
81.已知函数均为常数,当时取极大值,当时取极小值,则的取值范围是( )
A. B. C. D.
题组十:
82. 函数 ,的最大值是( )
A. B.-1 C.0 D.1
83.函数在上的最大值是( )
A. B. C. D.
84.已知e为自然对数的底数,函数y=ex-lnx在[1,e]的最小值为__________.
85.函数的最小值为( )
A. B. C. D.
86.已知(a是常数)在[-2,2]上有最大值11,那么在[-2,2]上f(x)的最小值是( )
A.-5 B.-11 C.-29 D.-37
87.函数在区间[0,]上的值域为________.
88.已知函数,对任意,不等式恒成立,则的取值范围为( )
A. B. C. D.
课堂检测:
89.函数在上的最大值和最小值分别是( )
A. B. C. D.
90.函数在区间(0,3)上的最大值为( )
A. B.1 C.2 D.
91.函数f(x)=x2-lnx的最小值为( )
A. B. C. D.
92.若函数在[-1,1]上有最大值3,则该函数在[-1,1]上的最小值是( )
A. B.0 C. D.1
题组十一:
93.已知是自然对数的底数,不等于1的两正数满足,若,则的最小值为( )
A.-1 B. C. D.
94.已知函数若方程有两个不相等的实根,,则的最大值为____.
95.已知函数,且存在不同的实数x1,x2,x3,使得f(x1)=f(x2)=f(x3),则x1x2x3的取值范围是( )
A. B. C. D.
课堂检测:
96.已知,,若,则的最小值为( )
A.1 B.2 C. D.
97.已知函数,若,且,则的取值范围是( )
A. B. C. D.
98.若点在函数的图象上,则的最小值是( )
A. B. C. D.
三、课外作业:
1.已知函数,则的最大值为___________.
2.已知函数,当时,函数的最大值为_______ .
3.函数在上的最大值是________.
4.已知定义在上的函数,其导函数的大致图象如图所示,则下列叙述正确的是( )
① ;
②函数在处取得极小值,在处取得极大值;
③函数在处取得极大值,在处取得极小值;
④函数的最小值为.
A.③ B.①② C.③④ D.④
5.设定义在上的可导函数的导函数的图象如下所示,则的极值点的个数为( )
A.1 B.2 C.3 D.4
6.已知函数的图象在点处的切线斜率为-3,则的极大值点为( )
A. B.-2 C. D.2
7.已知,是的导数,和单调性相同的区间是( )
A. B.和 C. D.
8.函数的递增区间是( )
A. B. C. D.
9.函数在上 ( ).
A.是增函数 B.是减函数 C.有最大值 D.有最小值
10.若函数f(x)=ax3+x恰有3个单调区间,则a的取值范围为________.
11.若函数不是单调函数,则实数的取值范围是( ).
A.[0,+∞) B.(﹣∞,0] C.(﹣∞,0) D.(0,+∞)
12.已知是定义在上的函数,若且,则的解集为()
A. B. C. D.
13.若,则
A. B. C. D.
14.函数 (,则( )
A. B. C. D.大小关系不能确定
15.若函数为奇函数,则的极大值点为( )
A. B. C. D.
16.设函数的导函数为,且满足,则时,( )
A.有极大值,无极小值 B.有极小值,无极大值 C.既有极大值又有极小值 D.既无极大值也无极小值
17.函数y=2x3-3x2( )
A.在x=0处取得极大值0,但无极小值 B.在x=1处取得极小值-1,但无极大值
C.在x=0处取得极大值0,在x=1处取得极小值-1 D.以上都不对
18.已知、、、,从这四个数中任取一个数使函数有极值点的概率为( )
A. B. C. D.1
19.等差数列中的分别是函数的两个不同极值点,则为( )
A. B.2 C.-2 D.-
20.设函数有两个极值点,且,,则点
在平面上所构成区域的面积为( )
A. B. C. D.
21.若,函数有两个极值点,则的取值范围为( )
A. B. C. D.
22.函数的最大值是______________.
23.已知函数的最小值为2,则___________.
一轮复习专题3.2 导数的应用(解析版)教案: 这是一份一轮复习专题3.2 导数的应用(解析版)教案,共27页。教案主要包含了必备知识,考点题型等内容,欢迎下载使用。
一轮复习专题5.3 复数(原卷版)教案: 这是一份一轮复习专题5.3 复数(原卷版)教案,共5页。教案主要包含了题型训练等内容,欢迎下载使用。
一轮复习专题7.2 线性规划(原卷版)教案: 这是一份一轮复习专题7.2 线性规划(原卷版)教案,共5页。教案主要包含了必备知识,题组训练等内容,欢迎下载使用。












