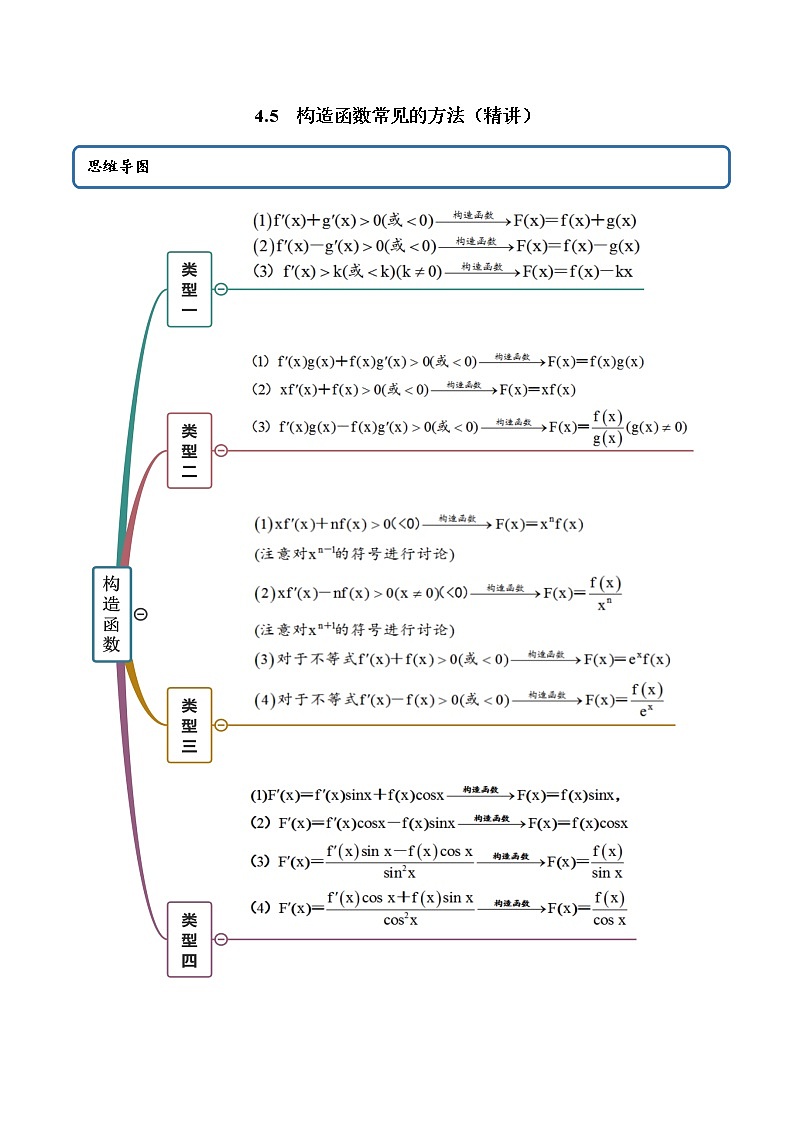
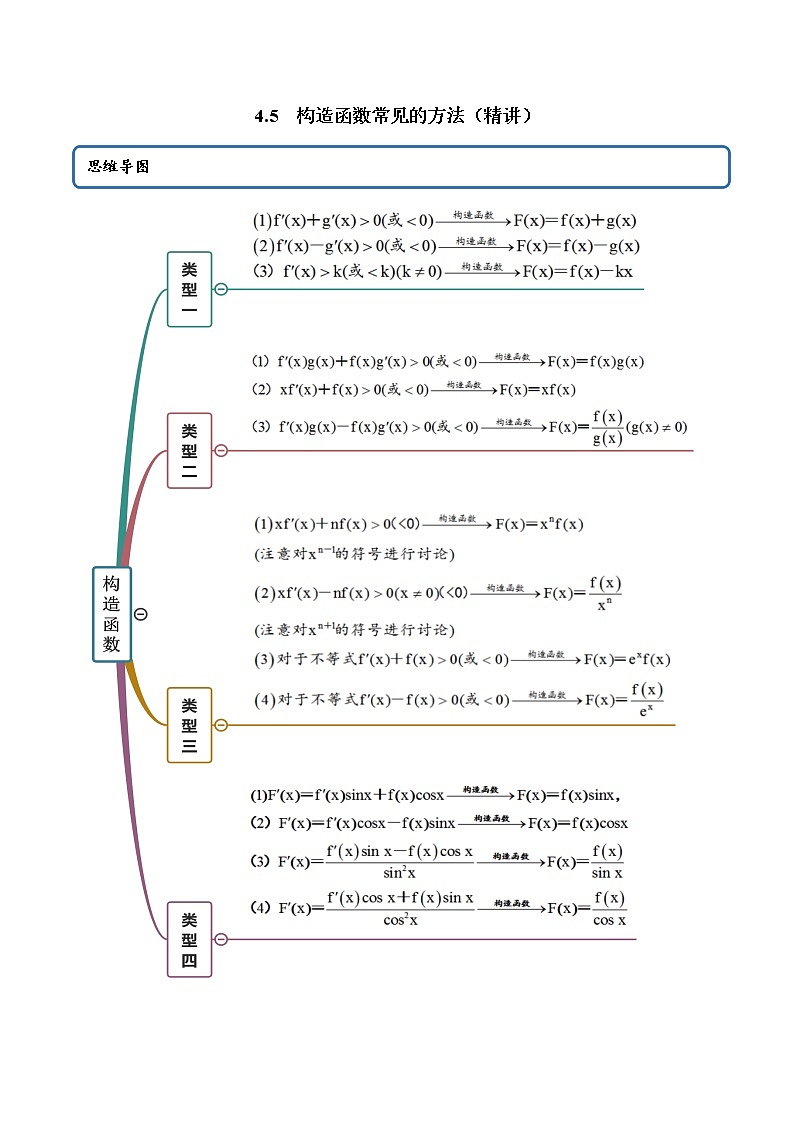
4.5 构造函数常见的方法（精讲+精练+原卷+解析）

这是一份4.5 构造函数常见的方法（精讲+精练+原卷+解析），共32页。主要包含了乘除法构造函数，三角函数型构造函数等内容，欢迎下载使用。

常见考法
考法一 加减法模型构造函数
【例1】（1）（2021·全国高三）设函数是奇函数的导函数，.当时，，则使得成立的的取值范围是（ ）
B．
C． D．
（2）（2021·青海西宁市）已知定义在R上的函数满足，且的导函数满足，则不等式的解集为（ ）
A．B．
C．D．或
【一隅三反】
1．（2021·漠河市高级中学）已知是定义在上的奇函数，是函数的导函数且在上，若，则实数的取值范围为（ ）
A．B．
C．D．
2．（2021·全国高三专题练习）已知定义在上的函数满足，对恒有，则的解集为（ ）
A． B．
C． D．
3．（2021·江苏南通市）已知定义域为的函数满足，，其中为导函数，则满足不等式的解集为（ ）
A． B．
C． D．
4．（2021·全国高三）函数是定义在上的函数，且为的导函数，若，则不等式的解集是________．
考法二 乘除法构造函数
【例2】（1）（2021·内蒙古锡林郭勒盟）设函数是函数的导函数，，，且，则不等式的解集为（ ）
A．B．
C．D．
（2）（2021·湖南益阳市·高三二模）已知定义在R上的奇函数f(x)，其导函数为，当x>0时，f(x)+x>0，且，则不等式(x2﹣2x)f(x)