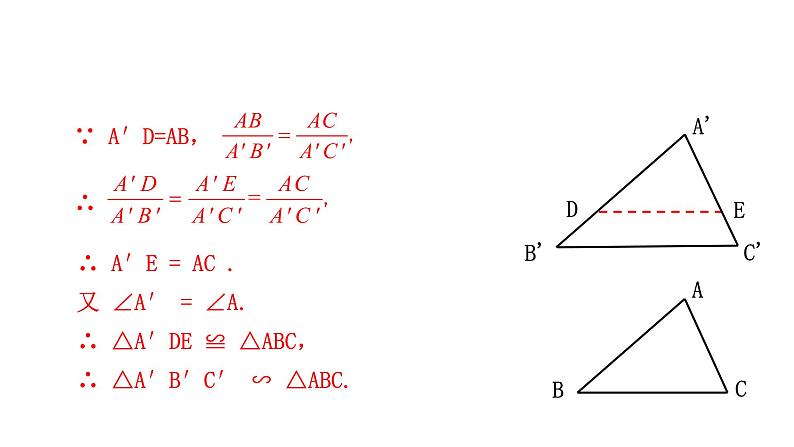
初中人教版第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定课文配套ppt课件

这是一份初中人教版第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定课文配套ppt课件，共21页。PPT课件主要包含了教学目标，回顾旧知，合作探究，有同样的结论，符号语言，归纳总结，思考3，典例精析，趁热打铁，∵∠1＝∠2等内容，欢迎下载使用。

1. 探索“两边成比例且夹角相等的两个三角形相似”的判定定理.2. 会根据边和角的关系来判定两个三角形相似，并进行相关计算. (重点、难点)
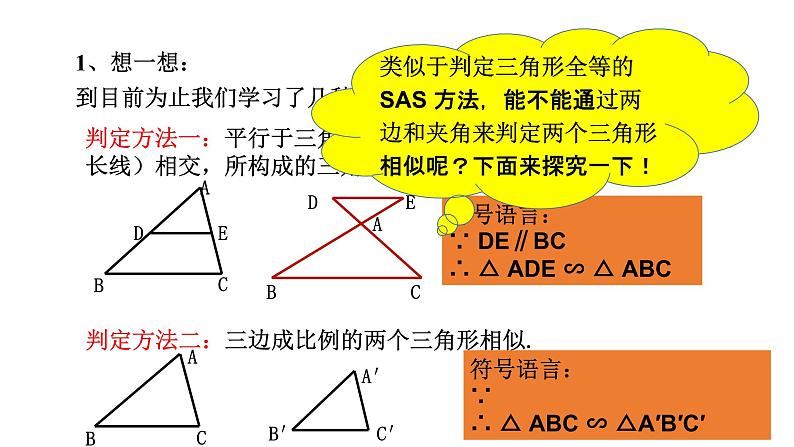
1、想一想：到目前为止我们学习了几种相似三角形的判定方法？
符号语言：∵ DE∥BC∴ △ ADE ∽ △ ABC
判定方法一：平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似。
判定方法二：三边成比例的两个三角形相似.
符号语言：∵ ∴ △ ABC ∽ △A′B′C′
类似于判定三角形全等的 SAS 方法，能不能通过两边和夹角来判定两个三角形相似呢？下面来探究一下！
思考1：改变 k 和∠A 的值的大小，是否有同样的结论？
思考2：你能证明这一结论吗？
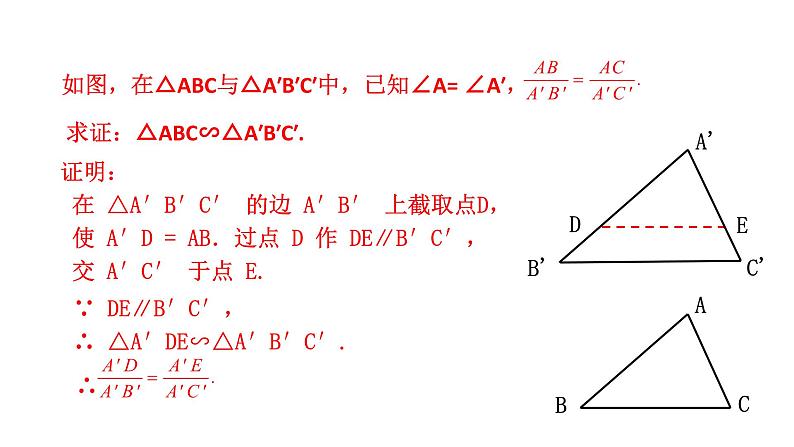
如图，在△ABC与△A′B′C′中，已知∠A= ∠A′，
证明： 在 △A′B′C′ 的边 A′B′ 上截取点D， 使 A′D = AB．过点 D 作 DE∥B′C′， 交 A′C′ 于点 E.
∵ DE∥B′C′，∴ △A′DE∽△A′B′C′.
求证：△ABC∽△A′B′C′.
∴ A′E = AC . 又 ∠A′ = ∠A.∴ △A′DE ≌ △ABC， ∴ △A′B′C′ ∽ △ABC.
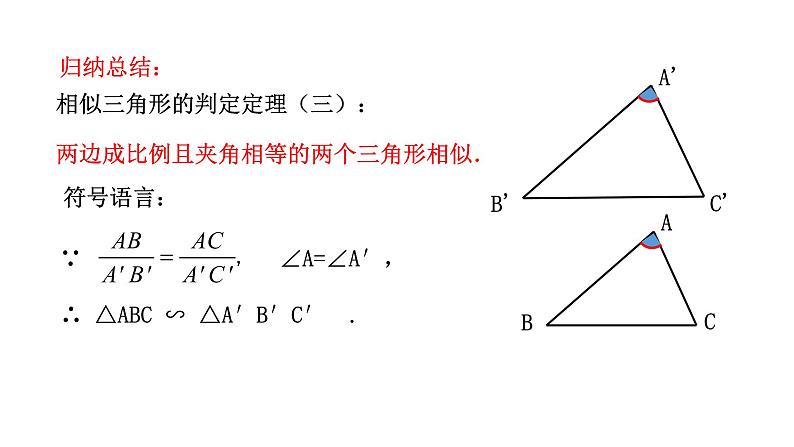
相似三角形的判定定理（三）：两边成比例且夹角相等的两个三角形相似．
∴ △ABC ∽ △A′B′C′ .
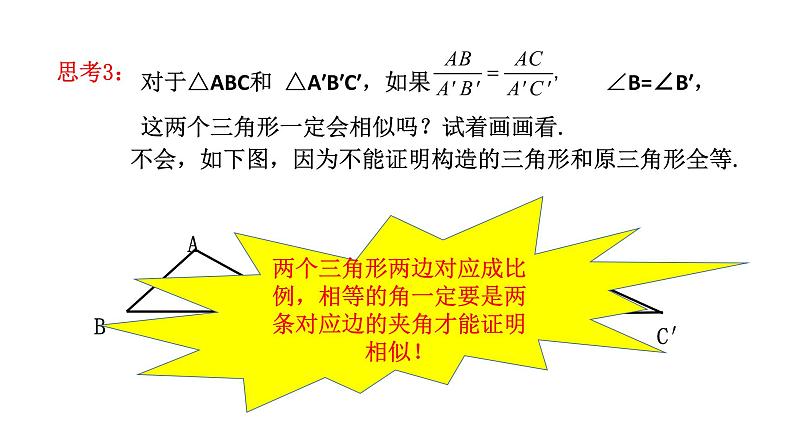
对于△ABC和 △A′B′C′，如果 ∠B=∠B′， 这两个三角形一定会相似吗？试着画画看.
不会，如下图，因为不能证明构造的三角形和原三角形全等.
两个三角形两边对应成比例，相等的角一定要是两条对应边的夹角才能证明相似！
例1、根据下列条件，判断 △ABC 和 △A′B′C′ 是否相似，并说明理由： ∠A=120°，AB=7 cm，AC=14 cm， ∠A′=120°，A′B′=3 cm ，A′C′=6 cm．
又 ∠A′ = ∠A，∴ △ABC ∽ △A′B′C′.
1、判断图中△AEB和△FEC是否相似？
∴△AEB∽△FEC
2. 在 △ABC 和 △DEF 中，∠C =∠F=65°，AC = 2 cm，BC = 3 cm，DF =1.2 cm，EF =1.8 cm. 求证：△DEF∽△ABC.
证明：∵ AC = 2 cm，BC = 3 cm，DF = 1.2 cm，EF = 1.8 cm，
又 ∵∠C =∠F = 65°，∴ △DEF ∽△ABC.
3、如图，△ABC 与 △ADE 都是等腰三角形，AD=AE，AB=AC， ∠DAB=∠CAE. 求证：△ABC ∽△ADE.
证明：∵ △ABC 与 △ADE 都是等腰三角形，∴ AD =AE，AB = AC，
又 ∵∠DAB = ∠CAE，∴ ∠DAB +∠BAE = ∠CAE +∠BAE，即 ∠DAE =∠BAC，∴△ABC ∽ △ADE.
(1) 两个等边三角形相似 ( )(2) 两个直角三角形相似 ( )(3) 两个等腰直角三角形相似( )(4) 有一个角是50°的两个等腰三角形相似 ( )(5)两条直角边成比例的两个直角三角形相似 （ ）
2、一个直角三角形的两边长分别为3和6,另一个直角三角形的两边长分别为2和4,那么这两个直角三角形（ ）相似。 A、 一定 B、 一定不 C、可能 D、无法判断
3、如图，D 是 △ABC 一边 BC 上一点，连接 AD，使△ABC ∽ △DBA的条件是 ( ) A. AC : BC=AD : BD B. AC : BC=AB : AD C. AB2 = CD · BC D. AB2 = BD · BC
解：∵ AE=1.8，AC=2.4，
4、如图，D，E分别是 △ABC 的边 AC，AB 上的点，AE=1.8，AC=2.4，BC=3，且 ，求 DE 的长.
又∵∠EAD=∠CAB，∴ △ADE ∽△ABC，
知识点拨：找对应边是关键。
5、 如图，在四边形 ABCD 中，已知 ∠B =∠ACD，AB=6，BC=4， AC=5，CD= ，求 AD 的长．
又∵∠B=∠ACD， ∴ △ABC ∽ △DCA，
6、如图，点D是 △ABC 的边AB 上的点，满足求证： △ACD ∽△ABC.
证明： ∵ CD 是边 AB 上的高， ∴ ∠ADC =∠CDB =90°.
∴△ADC ∽△CDB.∴ ∠ACD =∠B.∴ ∠ACB =∠ACD +∠BCD =∠B +∠BCD = 90°.
7、如图，在 △ABC 中，CD 是边 AB 上的高，且 ， 求证： ∠ACB=90°．
思考:图中是否还有相似三角形?找找看！
8、如图，四边形ABCD的对角线AC和BD相较于点O，其中OA=1，OB=1.5，OC=3，OD=2；求证： △OAD ∽△OBC
知识点拨：当 △ADP ∽△ACB 时，AP : AB =AD : AC ，∴ AP : 12 =6 : 8 ，解得 AP = 9；当 △ADP ∽△ABC 时，AD : AB =AP : AC ，∴ 6 : 12 = AP : 8 ，解得 AP = 4. ∴ 当 AP 的长度为 4 或 9 时，△ADP 和 △ABC 相似．
9、如图，已知 △ABC中，D 为边 AC 上一点，P 为边AB上一点，AB = 12，AC = 8，AD = 6，当 AP 的长度为 时，△ADP 和 △ABC 相似.