人教版九年级下册27.2.2 相似三角形的性质多媒体教学课件ppt

这是一份人教版九年级下册27.2.2 相似三角形的性质多媒体教学课件ppt，共53页。PPT课件主要包含了学习目标，导入新知，角平分线，合作探究，相似比为，对应高的比，对应中线的比，对应角平分线的比，∴∠B∠E，或48等内容，欢迎下载使用。

1.在理解相似三角形特征的基础上，掌握相似三角形对应高、对应中线、对应角平分线、周长、面积的比等性质，并运用其进行计算与推理。2.通过实践体会相似三角形的性质，会用性质与判定解决相关的问题。
相似三角形的判定方法有哪几种？
1.对应边成比例，对应角相等的两个三角形相似.
2.平行于三角形一边，与另外两边相交所构成的三角形与原三角形相似.
3. 三边对应成比例的两三角形相似.
4. 两边成比例且夹角相等的两个三角形相似.
5. 两角分别相等的两个三角形相似.
6. 两边对应成比例的两直角三角形相似.
三角形除了三个角,三条边外,还有哪些要素?
【思考】如果两个三角形相似，那么它们的这些要素有一些怎样的性质呢?
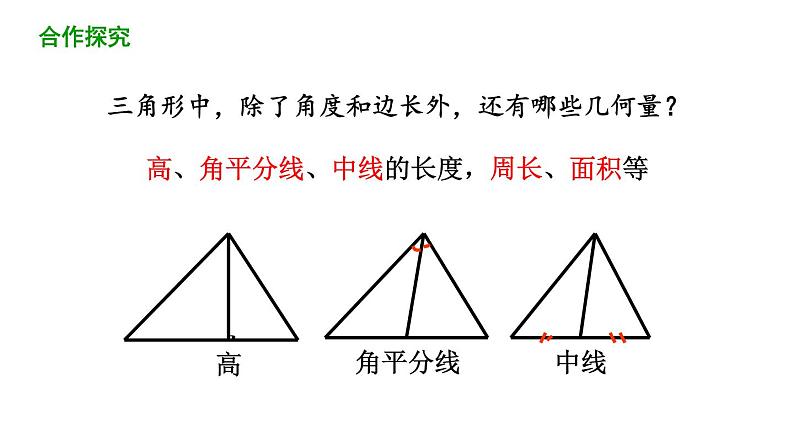
三角形中，除了角度和边长外，还有哪些几何量？
高、角平分线、中线的长度，周长、面积等
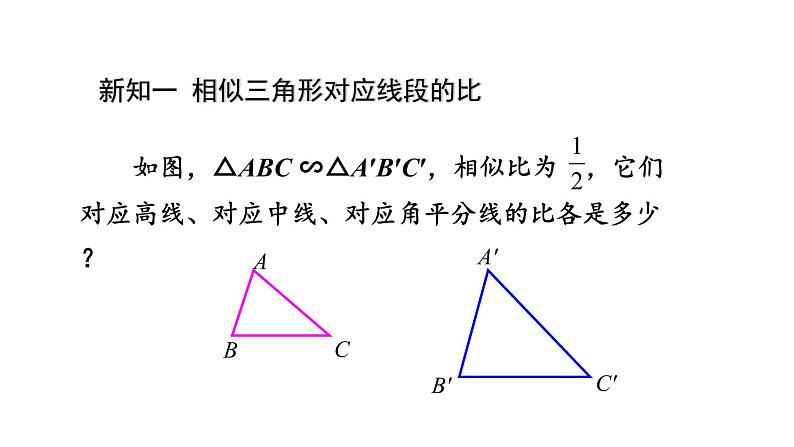
新知一 相似三角形对应线段的比
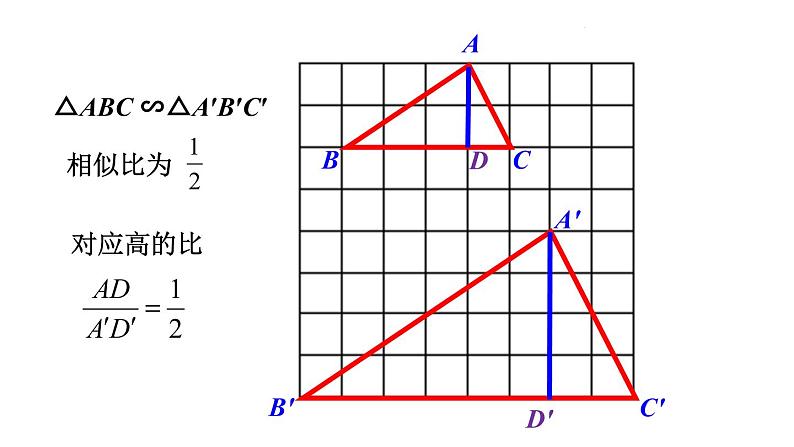
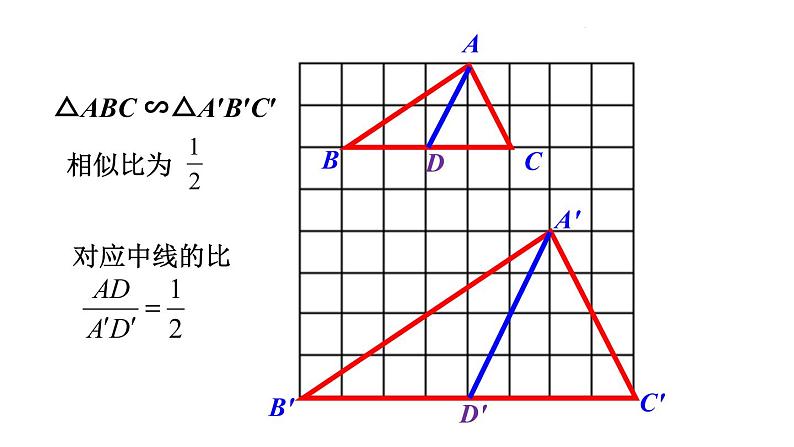
△ABC ∽△A′B′C′
如图， △ABC ∽△A′B′C′ ，若相似比为k ，它们对应高、对应中线、对应角平分线的比又各是多少？
相似三角形对应高的比等于相似比
∵△ A′B′C′∽△ABC，
又∵ ∠A'D′B' =∠ADB =90°,
∴△A′B′D′∽△ABD
如图，△A′B′C′ ∽△ABC，相似比为k，分别作BC，B′C′上的高AD，A′D′． 求证：
证明：∵△ABC∽△DEF.
相似三角形对应中线的比等于相似比.
又∵AM、DN分别是△ABC和△DEF的中线.
∴△ABM∽△DEN.
△ABC∽△DEF. AM、DN分别为中线
∴BC=2BM,EF=2EN,
证明：∵△ABC∽△DEF. ∴∠B =∠E, ∠BAC=∠EDF.又∵AM、DN分别是∠BAC和∠EDF的角平分线.
相似三角形对应角平分线的比等于相似比.
△ABC∽△DEF. AM、DN分别为角平分线
∴∠BAM=∠EDN.
∴△AMB∽△DNE.
相似三角形对应中线、角平分线的比也等于相似比.
相似三角形对应高的比等于相似比.
一般地，我们有： 相似三角形对应线段的比等于相似比.

解：∵ △ABC ∽△DEF， 　
例1 已知 △ABC∽△DEF，BG、EH 分别是 △ABC和 △DEF 的角平分线，BC = 6 cm，EF = 4cm，BG = 4.8 cm. 求 EH 的长.
故 EH 的长为 3.2 cm.
典例精析1 利用相似三角形对应线段的比求线段的长度
1.相似三角形对应边的比为2∶3,那么相似比为________,对应角的角平分线的比为 .
2.两个相似三角形对应边上的高的比为1∶4 , 若一个三角形的最长边是为12，则另一个三角形的最长边是_______.
相似三角形的周长比也等于相似比吗？为什么？
相似三角形周长的比等于相似比.
∵△ABC ∽△A′B′C′
∴AB=kA′B′，BC=kB′C′，AC=kA′C′
相似三角形的周长比等于相似比
∵△ABC ∽△A′B′C′，
3.相似三角形对应边的比为2∶5,那么周长比为________.
4.两个相似三角形周长的比为1∶7 , 则它们的相似比为_______,对应边上角平分线的比为_______.
如图，△ABC ∽△A′B′C′，相似比为k，它们的面积比是多少？
新知二 相似三角形面积的比
相似三角形性质定理:
相似三角形面积的比等于相似比的平方.
∵△ABC ∽△A′B′C′，相似比为k ，
5. 已知两个三角形相似，请完成下列表格：
解：在 △ABC 和 △DEF 中， ∵ AB=2DE，AC=2DF，
∴ △DEF ∽ △ABC ，相似比为 1 : 2.
典例精析1 利用相似三角形面积的比求面积或线段
6. 如果两个相似三角形的面积之比为 4 : 9，较大三角形一边上的高为 18，则较小三角形对应边上的高为______.
例3 如图，D，E 分别是 AC，AB 上的点，已知△ABC 的面积为100 cm2，且 ，求四边形 BCDE 的面积. 　
∴ △ADE ∽△ABC.
∵ 它们的相似比为 3 : 5，∴ 面积比为 9 : 25.
典例精析2 利用相似三角形面积的比求多边形的面积(比）
又∵ △ABC 的面积为 100 cm2，
∴ △ADE 的面积为 36 cm2 .
∴ 四边形 BCDE 的面积为100－36 = 64 (cm2).
7. 如图，这是圆桌正上方的灯泡 （点A ） 发出的光线照射桌面形成阴影的示意图，已知桌面的直径为 1.2米，桌面距离地面为 1 米，若灯泡距离地面 3 米，则地面上阴影部分的面积约为多少 (结果保留两位小数)？
解：∵ FH = 1 米，AH = 3 米，桌面的直径为 1.2 米， ∴ AF = AH－FH = 2 (米)，DF = 1.2÷2 = 0.6(米). ∵DF∥CH，∴△ADF ∽△ACH，
解得 CH = 0.9米.
答：地面上阴影部分的面积为 2.54 平方米.
∴ 阴影部分的面积为：
2．(4分)如图，在△ABC中，DE∥BC，AH是△ABC的角平分线，交DE于点G，DE∶BC＝2∶3，那么AG∶GH等于______________．
4．(3分)(铜仁中考)已知△FHB∽△EAD，它们的周长分别为30和15，且FH＝6，则EA的长为( )A．3 B．2 C．4 D．5
6．(4分)已知两个相似三角形的最短边的长分别为5和3，且它们周长的差为12，则较大三角形的周长为__________．
8．(3分)如图，在平行四边形ABCD中，点E在边DC上，DE∶EC＝3∶1，连接AE交BD于点F，则△DEF的面积与△BAF的面积之比为( )A．3∶4 B．9∶16 C．4∶9 D．1∶3
9．(4分)如图，在△ABC中，EF∥BC，AB＝3AE，若S四边形BCFE＝16，则S△ABC＝____．
10．(9分)(教材P38例3变式)已知△ABC∽△A′B′C′，AB边上的中线CD＝4 cm，A′B′边上的中线C′D′＝8 cm，△ABC的周长为20 cm，△A′B′C′的面积是64 cm2，求：(1)△A′B′C′的周长；(2)△ABC的面积．
相似三角形对应线段的比等于相似比
相似三角形面积的比等于相似比的平方
2．一张等腰三角形纸片，底边长15 cm，底边上的高为22.5 cm.现沿底边依次从下往上裁剪宽度均为3 cm的矩形纸条，如图所示．已知剪得的纸条中有一张是正方形，则这张正方形纸条是( )A．第4张 B．第5张 C．第6张 D．第7张
3．如图，点M是△ABC内一点，过点M分别作直线平行于△ABC的各边，所形成的三个小三角形△1，△2，△3(图中阴影部分)的面积分别是1，4，9，则△ABC的面积是_________．
4．如图，小明拿着一把厘米刻度尺，站在距电线杆约30 m的地方，把手臂向前伸直，刻度尺竖直，刻度尺上18个刻度恰好遮住电线杆，已知小明手臂长约 60 cm，小明能求出电线杆的高度吗？若能，请你替小明写出求解过程．
5．如图，在△ABC中，D，E两点分别在AB，AC上，点F在DE上，G，H两点在BC上，且DE∥BC，FG∥AB，FH∥AC，若BG∶GH∶HC＝4∶6∶5，求△ADE与△FGH的面积之比．
6．如图，在△ABC中，BC＞AC，点D在BC上，且CA＝CD，∠ACB的平分线交AD于点F，E是AB的中点．(1)求证：EF∥BD；(2)若∠ACB＝60°，AC＝8，BC＝12，求四边形BDFE的面积．