2021学年22.3 实际问题与二次函数示范课课件ppt

这是一份2021学年22.3 实际问题与二次函数示范课课件ppt，共17页。PPT课件主要包含了复习引入，新课讲解，Sl30-l，-2x，问题5如何求最值，＜x≤18，不正确，知识要点，随堂即练，几何面积最值问题等内容，欢迎下载使用。
1.分析实际问题中变量之间的二次函数关系.（难点）2.会运用二次函数求实际问题中的最大值或最小值.3.能应用二次函数的性质解决图形中最大面积问题.（重点）
写出下列抛物线的开口方向、对称轴和顶点坐标，并写出其最值.（1）y=x2-4x-5; (配方法) (2)y=-x2-3x+4.(公式法)
解：（1）开口方向：向上；对称轴：x=2；顶点坐标：（2，-9）；最小值：-9；
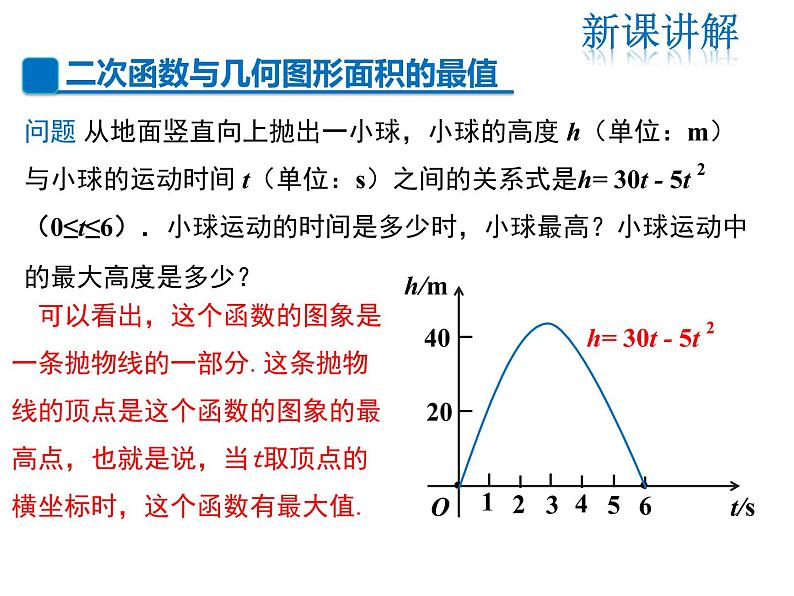
问题 从地面竖直向上抛出一小球，小球的高度 h（单位：m）与小球的运动时间 t（单位：s）之间的关系式是h= 30t - 5t 2 （0≤t≤6）．小球运动的时间是多少时，小球最高？小球运动中的最大高度是多少？
可以看出，这个函数的图象是一条抛物线的一部分.这条抛物线的顶点是这个函数的图象的最高点，也就是说，当t取顶点的横坐标时，这个函数有最大值.
二次函数与几何图形面积的最值
　　如何求出二次函数 y = ax 2 + bx + c 的最小（大）值？
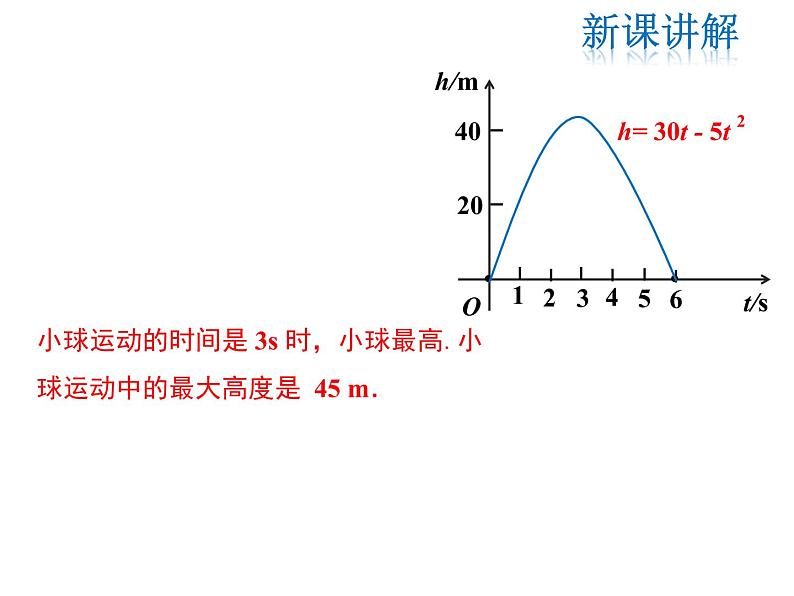
小球运动的时间是 3s 时，小球最高.小球运动中的最大高度是 45 m．
问题1 矩形面积公式是什么？
问题2 如何用l表示另一边？
问题3 面积S的函数关系式是什么？
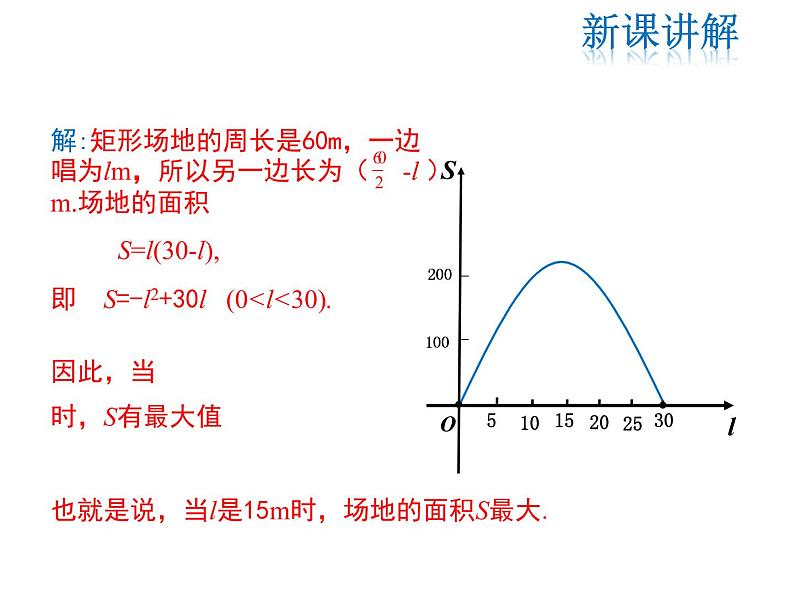
解:矩形场地的周长是60m，一边唱为lm，所以另一边长为（ -l ）m.场地的面积
即 S=-l2+30l (0