

人教版九年级上册数学--期中数学试卷附答案(模拟测试卷)
展开期中数学试卷2
一、选择题:本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
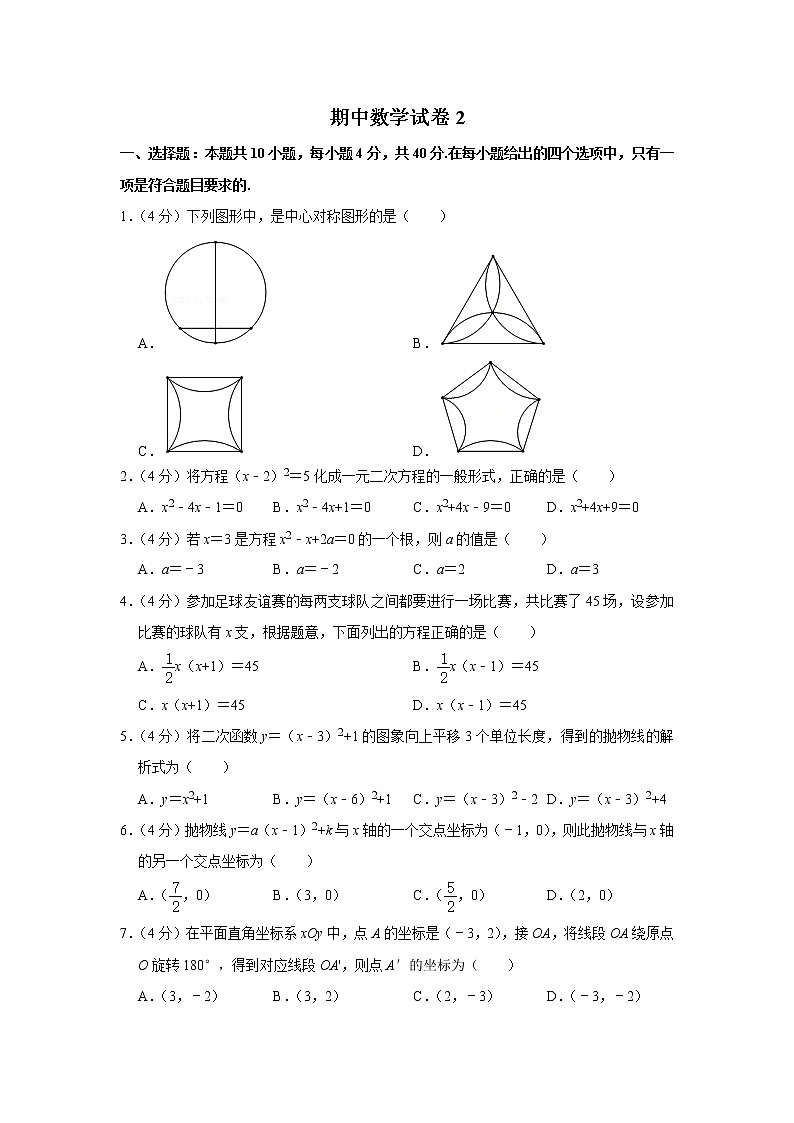
1.(4分)下列图形中,是中心对称图形的是( )
A. B.
C. D.
2.(4分)将方程(x﹣2)2=5化成一元二次方程的一般形式,正确的是( )
A.x2﹣4x﹣1=0 B.x2﹣4x+1=0 C.x2+4x﹣9=0 D.x2+4x+9=0
3.(4分)若x=3是方程x2﹣x+2a=0的一个根,则a的值是( )
A.a=﹣3 B.a=﹣2 C.a=2 D.a=3
4.(4分)参加足球友谊赛的每两支球队之间都要进行一场比赛,共比赛了45场,设参加比赛的球队有x支,根据题意,下面列出的方程正确的是( )
A.x(x+1)=45 B.x(x﹣1)=45
C.x(x+1)=45 D.x(x﹣1)=45
5.(4分)将二次函数y=(x﹣3)2+1的图象向上平移3个单位长度,得到的抛物线的解析式为( )
A.y=x2+1 B.y=(x﹣6)2+1 C.y=(x﹣3)2﹣2 D.y=(x﹣3)2+4
6.(4分)抛物线y=a(x﹣1)2+k与x轴的一个交点坐标为(﹣1,0),则此抛物线与x轴的另一个交点坐标为( )
A.(,0) B.(3,0) C.(,0) D.(2,0)
7.(4分)在平面直角坐标系xOy中,点A的坐标是(﹣3,2),接OA,将线段OA绕原点O旋转180°,得到对应线段OA',则点A′的坐标为( )
A.(3,﹣2) B.(3,2) C.(2,﹣3) D.(﹣3,﹣2)
8.(4分)如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,连接CO,AD,∠BAD=α,则∠OCD的度数( )
A.2α B.3α C.90°﹣α D.90°﹣2α
9.(4分)如图,在△ABC中,∠ABC=α,将△ABC绕点B逆时针旋转得到△A′BC′,使点C的对应点C′恰好落在边AB上,若CA=CB,则∠CAA′的度数是( )
A.90°﹣α B.90°﹣α C.90°+α D.90°+α
10.(4分)若二次函数y=(x﹣3)2+2m,在自变量x满足m≤x≤m+2的情况下,与其对应的函数值y的最小值为5,则m的值为( )
A.﹣2或2 B.﹣2或 C.2或 D.﹣2或2或
二、填空题:本题共6小题,每小题4分,共24分
11.(4分)抛物线y=2(x﹣6)2+9的顶点坐标为 .
12.(4分)如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=3,则BB′的长为 .
13.(4分)若x1,x2是一元二次方程4x2﹣5x+1=0的两个根,则x1+x2+x1•x2的值为 .
14.(4分)如图,在⊙O中,直径AB垂直弦CD于点E,若AE=4,OE=1,则CD的长为 .
15.(4分)已知(a2+b2)(a2+b2﹣4)=7,则a2+b2的值为 .
16.(4分)如图,在⊙O中,直径AB=2,延长AB至C,使BC=OB,点D在⊙O上运动,连接CD,将CD绕点C顺时针旋转90°得到CE,连接OE,则线段OE的最大值为 .
三、解答题:本题共9小题,共86分.解答应写出文字说明、证明过程或演算步骤。
17.(8分)解方程:x(x﹣3)+x﹣3=0.
18.(8分)已知关于x的一元二次方程mx2+4x+2=0有两个不相等的实数根,求m的取值范围.
19.(8分)已知抛物线y=ax2+bx+c过A(0,0),B(1,9),C(2,26)三点,求该抛物线的解析式.
20.(8分)如图,四边形ABCD是矩形.求证:A,B,C,D四点在同一个圆上.
21.(8分)如图,点M是等边三角形ABC内的一点,连接AM,CM.
(1)尺规作图:作出△ACM绕点A顺时针旋转60°得到的△ABN;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若∠ACM+∠CAM=60°,求证:C,M,N三点共线.
22.(10分)如图,在⊙O中,直径AB和弦CD相交于点E,∠A=30°,∠AEC=∠OCE+30°.
(1)求证:AC=AE;
(2)若AC=2,求CD的长.
23.(10分)某商品现在的售价为每件50元,每星期可卖出200件.市场调查反映:如果调整价格,每涨价1元,每星期要少卖出5件;每降价1元,每星期可多卖出25件.已知商品的进价为每件30元,问如何定价才能使一星期利润最大?最大利润是多少?
24.(12分)如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,点D是BC边上一动点,连接AD,把AD绕点A逆时针旋转90°得到AE,连接CE,DE.
(1)求∠ECD的度数;
(2)取DE的中点F,连接CF.分别延长CF,BA,相交于点G,如备用图所示.
①求证:GF=CF;
②当BD=3CD时,求AG的长.
25.(14分)已知二次函数y=x2+bx+b﹣1,其中b为常数.
(1)当y=0时,求x的值;(用含b的式子表示)
(2)抛物线y=x2+bx+b﹣1与x轴交于A,B两点(点A在点B的左侧),过点E(4,2)作直线交抛物线于P,Q两点,其中点P在第一象限,点Q在第四象限,连接AP,AQ分别交y轴于点M(0,m),N(0,n).
①当b<2时,求点P的横坐标xp的值;(用含m,b的式子表示)
②当b=﹣3时,求证:OM•ON是一个定值.
2020-2021学年福建省福州市仓山区九年级(上)期中数学试卷
参考答案与试题解析
一、选择题:本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(4分)下列图形中,是中心对称图形的是( )
A. B.
C. D.
【解答】解:选项A、B、D不能找到这样的一个点,使图形绕某一点旋转180°后和原图形完全重合,所以不是中心对称图形,
选项C能找到这样的一个点,使图形绕某一点旋转180°后和原图形完全重合,所以是中心对称图形,
故选:C.
2.(4分)将方程(x﹣2)2=5化成一元二次方程的一般形式,正确的是( )
A.x2﹣4x﹣1=0 B.x2﹣4x+1=0 C.x2+4x﹣9=0 D.x2+4x+9=0
【解答】解:(x﹣2)2=5,
x2﹣4x+4﹣5=0,
x2﹣4x﹣1=0,
即将方程(x﹣2)2=5化成一般形式为x2﹣4x﹣1=0,
故选:A.
3.(4分)若x=3是方程x2﹣x+2a=0的一个根,则a的值是( )
A.a=﹣3 B.a=﹣2 C.a=2 D.a=3
【解答】解:∵x=3是方程x2﹣x+2a=0的一个根,
∴32﹣3+2a=0,
解得 a=3.
故选:D.
4.(4分)参加足球友谊赛的每两支球队之间都要进行一场比赛,共比赛了45场,设参加比赛的球队有x支,根据题意,下面列出的方程正确的是( )
A.x(x+1)=45 B.x(x﹣1)=45
C.x(x+1)=45 D.x(x﹣1)=45
【解答】解:依题意得:x(x﹣1)=45.
故选:B.
5.(4分)将二次函数y=(x﹣3)2+1的图象向上平移3个单位长度,得到的抛物线的解析式为( )
A.y=x2+1 B.y=(x﹣6)2+1 C.y=(x﹣3)2﹣2 D.y=(x﹣3)2+4
【解答】解:将二次函数y=(x﹣3)2+1的图象向上平移3个单位长度,得到的抛物线的解析式为:y=(x﹣3)2+1+3,即y=(x﹣3)2+4.
故选:D.
6.(4分)抛物线y=a(x﹣1)2+k与x轴的一个交点坐标为(﹣1,0),则此抛物线与x轴的另一个交点坐标为( )
A.(,0) B.(3,0) C.(,0) D.(2,0)
【解答】解:∵y=a(x﹣1)2+k对称轴为x=1,
又∵抛物线y=a(x﹣1)2+k与x轴的一个交点坐标为(﹣1,0),
∴两个交点关于直线x=1对称,
设另一个交点是x1,
则x1+(﹣1)=2,
解得:x1=3,
∴另一个交点为(3,0).
故选:B.
7.(4分)在平面直角坐标系xOy中,点A的坐标是(﹣3,2),接OA,将线段OA绕原点O旋转180°,得到对应线段OA',则点A′的坐标为( )
A.(3,﹣2) B.(3,2) C.(2,﹣3) D.(﹣3,﹣2)
【解答】解:由题意,A与A′关于原点对称,
∵A(﹣3,2),
∴A′(3,﹣2),
故选:A.
8.(4分)如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,连接CO,AD,∠BAD=α,则∠OCD的度数( )
A.2α B.3α C.90°﹣α D.90°﹣2α
【解答】解:连接OD,
∵AB是直径,CD是弦,AB⊥CD,
∴=,
∴∠BOC=∠BOD,
∵∠BAD=α,
∴∠BOD=2α,
∴∠COD=4α,
∵OC=OD,
∴∠OCD=(180°﹣4α)=90°﹣2α,
故选:D.
9.(4分)如图,在△ABC中,∠ABC=α,将△ABC绕点B逆时针旋转得到△A′BC′,使点C的对应点C′恰好落在边AB上,若CA=CB,则∠CAA′的度数是( )
A.90°﹣α B.90°﹣α C.90°+α D.90°+α
【解答】解:∵CA=CB,∠ABC=α,
∴∠ABC=∠CAB=α,
∵将△ABC绕点B逆时针旋转得到△A′BC′,
∴AB=A'B,∠ABC=∠A'BA=α,
∴∠BAA'=,
∴∠CAA'=∠CAB+∠BAA'=90°+α,
故选:C.
10.(4分)若二次函数y=(x﹣3)2+2m,在自变量x满足m≤x≤m+2的情况下,与其对应的函数值y的最小值为5,则m的值为( )
A.﹣2或2 B.﹣2或 C.2或 D.﹣2或2或
【解答】解:∵二次函数y=(x﹣3)2+2m,
∴图象开口向上,对称轴为直线x=3,
①当3<m时,
在自变量x的值满足m≤x≤m+2的情况下,y随x的增大而增大,
∴当x=m时,y=(m﹣3)2+2m=m2﹣4m+9为最小值,
∵m2﹣4m+9=5,
解得m=2,不合题意;
②当m≤3≤m+2时,
∴x=3,y=(x﹣3)2+2m=2m为最小值,
∴2m=5,解得,m=;
③当3>m+2,即m<1,
在自变量x的值满足m≤x≤m+2的情况下,y随x的增大而减小,
故当x=m+2时,y=(m+2﹣3)2+2m=m2+1为最小值,
∴m2+1=5.解得,m1=2(舍去),m2=﹣2;
综上,m的值为或﹣2.
故选:B.
二、填空题:本题共6小题,每小题4分,共24分
11.(4分)抛物线y=2(x﹣6)2+9的顶点坐标为 (6,9) .
【解答】解:二次函数y=2(x﹣6)2+9的图象的顶点坐标是(6,9).
故答案为:(6,9).
12.(4分)如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=3,则BB′的长为 12 .
【解答】解:∵在Rt△ABC中,∠B=30°,AC=3,
∴AB=2AC=6,
∵B与B'关于A中心对称,
∴BB′=2AB=12.
故答案为:12.
13.(4分)若x1,x2是一元二次方程4x2﹣5x+1=0的两个根,则x1+x2+x1•x2的值为 .
【解答】解:根据题意得x1+x2=,x1x2=,
所以x1+x2+x1•x2=+=.
故答案为:.
14.(4分)如图,在⊙O中,直径AB垂直弦CD于点E,若AE=4,OE=1,则CD的长为 4 .
【解答】解:连接OC,
∵AE=4,OE=1,
∴OC=OA=AE﹣OE=4﹣1=3,
在Rt△OCE中,CE===2,
∵AB⊥CD,
∴CD=2CE=4,
故答案为:4.
15.(4分)已知(a2+b2)(a2+b2﹣4)=7,则a2+b2的值为 2+ .
【解答】解:设x=a2+b2,且x≥0,
∵(a2+b2)(a2+b2﹣4)=7,
∴x(x﹣4)=7,
∴x2﹣4x=7,
∴x2﹣4x+4=11,
∴(x﹣2)2=11,
∴x=2+或x=2﹣(舍去),
即a2+b2=2+.
故答案为:2+.
16.(4分)如图,在⊙O中,直径AB=2,延长AB至C,使BC=OB,点D在⊙O上运动,连接CD,将CD绕点C顺时针旋转90°得到CE,连接OE,则线段OE的最大值为 2+1 .
【解答】解:如图,过点C作AC的垂线,在垂线上截取CF=CO,连接DF,
∴∠DCE=∠OCF=90°,
∴∠OCE=∠FCD,
又∵CD=CE,
∴△OCE≌△FCD(SAS),
∴OE=FD,
连接FO,并延长FO交圆于点H,FH即为FD最大值,
∵AB=2,OB=BC,
∴OC=CF=2,
∴OF=2,
∴FH=OF+OH=2+1,
∴OE最大值=DF最大值=FH=2+1,
故答案为:2+1.
三、解答题:本题共9小题,共86分.解答应写出文字说明、证明过程或演算步骤。
17.(8分)解方程:x(x﹣3)+x﹣3=0.
【解答】解:分解因式得:(x﹣3)(x+1)=0,
可得x﹣3=0或x+1=0,
解得:x1=3,x2=﹣1.
18.(8分)已知关于x的一元二次方程mx2+4x+2=0有两个不相等的实数根,求m的取值范围.
【解答】解:∵关于x的一元二次方程mx2+4x+2=0有两个不相等的实数根,
∴m≠0且Δ>0,即42﹣4m×2>0,
解得m<2且m≠0.
∴当m<2且m≠0时,关于x的一元二次方程mx2+4x+2=0有两个不相等的实数根.
19.(8分)已知抛物线y=ax2+bx+c过A(0,0),B(1,9),C(2,26)三点,求该抛物线的解析式.
【解答】解:根据题意可得,
解得,
即抛物线的解析式为y=4x2+5x.
20.(8分)如图,四边形ABCD是矩形.求证:A,B,C,D四点在同一个圆上.
【解答】证明:连接AC、BD,交于点O,
∵四边形ABCD是矩形.
∴OA=OB=OC=OD,
∴A、B、C、D四点在以O为圆心、以AC为半径的同一个圆上.
21.(8分)如图,点M是等边三角形ABC内的一点,连接AM,CM.
(1)尺规作图:作出△ACM绕点A顺时针旋转60°得到的△ABN;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若∠ACM+∠CAM=60°,求证:C,M,N三点共线.
【解答】(1)解:如图,△ABN即为所求;
(2)证明:如图,连接MN,
由旋转可知:AM=AN,∠MAN=CAB=60°,
∴△AMN是等边三角形,
∴∠AMN=60°,
∵∠ACM+∠CAM=60°,
∴∠AMC=120°,
∴∠AMN+∠AMC=60°+120°=180°,
∴C,M,N三点共线.
22.(10分)如图,在⊙O中,直径AB和弦CD相交于点E,∠A=30°,∠AEC=∠OCE+30°.
(1)求证:AC=AE;
(2)若AC=2,求CD的长.
【解答】(1)证明:连接OC,
∵OA=OC,∠A=30°,
∴∠A=∠ACO=30°,
∴∠ACE=∠OCE+30°,
∵∠AEC=∠OCE+30°,
∴∠ACE=∠AEC,
∴AC=AE;
(2)过点O作OF⊥CD于点F,作OM⊥AC于点M,
∴CF=DF=CD,AM=CM=AC,
∵AC=2,
∴AM=,
∵∠A=30°,∠AMO=90°,
∴OM=OA,
∴AM====3,
∴OA=2,
由(1)知,∠ACE=∠AEC,
∴∠ACE=(180°﹣∠A)=(180°﹣30°)=75°,
∵∠ACO=∠A=30°,
∴∠OCF=75°﹣30°=45°,
∵∠OFC=90°,
∴∠COF=45°,
∴CF=OF,
∵OC=OA=2,
∴CF=OCsin45°=OC=,
∴CD=2.
23.(10分)某商品现在的售价为每件50元,每星期可卖出200件.市场调查反映:如果调整价格,每涨价1元,每星期要少卖出5件;每降价1元,每星期可多卖出25件.已知商品的进价为每件30元,问如何定价才能使一星期利润最大?最大利润是多少?
【解答】解:①设涨价x元,利润为y,
则y=(50﹣30+x)(200﹣5x)
=﹣5x2+100x+4000
=﹣5(x﹣10)2+4500,
∵﹣5<0,
∴当x=10时,y有最大值4500,
此时50+10=60(元),
每件定价为60元时利润最大;
②设每件降价a元,总利润为w,
则w=(50﹣30﹣a)(200+25a)
=﹣25a2+300a+4000
=﹣25(a﹣6)2+4900,
∵﹣25<0,
∴当a=6时,w有最大值4900,
此时50﹣6=44(元),
每件定价为44元时利润最大.
综上所述:每件定价为44元时利润最大,最大利润为4900元.
24.(12分)如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,点D是BC边上一动点,连接AD,把AD绕点A逆时针旋转90°得到AE,连接CE,DE.
(1)求∠ECD的度数;
(2)取DE的中点F,连接CF.分别延长CF,BA,相交于点G,如备用图所示.
①求证:GF=CF;
②当BD=3CD时,求AG的长.
【解答】(1)解:如图1中,
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠B,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=90°,
∴∠ACE=∠B=45°,
∴∠ECD=∠ACB=∠ACE=90°.
(2)①证明:如图2中,连接AF.
∵∠ECD=∠EAD=90°,EF=DF,
∴AF=CF=DF,
∴∠FAC=∠FCA,
∵∠ACG+∠G=90°,∠FAC+∠GAF=90°,
∴∠G=∠FAG,
∴FA=FG,
∵AF=FC,
∴FG=FC.
②解:如图3中,连接DG,GE.
∵DF=EF,GF=CF,
∴四边形CDGE是平行四边形,
∵CG=DE,
∴四边形CDGE是矩形,
∴∠CDG=90°,
∴AB=AC=2,∠BAC=90°,
∴BC=AB=4,∠B=45°
∵BD=3CD,
∴BD=DG=3,CD=1,
∴CG===,
∴AG===.
25.(14分)已知二次函数y=x2+bx+b﹣1,其中b为常数.
(1)当y=0时,求x的值;(用含b的式子表示)
(2)抛物线y=x2+bx+b﹣1与x轴交于A,B两点(点A在点B的左侧),过点E(4,2)作直线交抛物线于P,Q两点,其中点P在第一象限,点Q在第四象限,连接AP,AQ分别交y轴于点M(0,m),N(0,n).
①当b<2时,求点P的横坐标xp的值;(用含m,b的式子表示)
②当b=﹣3时,求证:OM•ON是一个定值.
【解答】解:(1)当y=0时,x2+bx+b﹣1=0,
∴(x+1)(x+b﹣1)=0,
∴x+1=0或x+b﹣1=0,
∴x1=﹣1,x2=1﹣b;
(2)①当b<2时,由(1)可知:x1=﹣1,x2=1﹣b,
∵b<2,
∴﹣b>﹣2,
∴1﹣b>﹣1,
∵点A在点B的左侧,
∴A(﹣1,0),
设直线AM的解析式为y=kx+a,
∵A(﹣1,0),M(0,m),
∴,
解得:,
∴直线AM的解析式为y=mx+m,
联立方程组,得:,
消去y,得:x2+(b﹣m)x+b﹣m﹣1=0,
由根与系数关系,得xA+xP=﹣(b﹣m)=m﹣b,
∴xP=m﹣b+1,
②证明:当b=﹣3时,二次函数解析式为y=x2﹣3x﹣4,
∴A(﹣1,0),B(4,0),
∵xP=m+4,
∴yP=(m+4)2﹣3(m+4)﹣4=m2+5m,
∴P(m+4,m2+5m),
直线AN的解析式为:y=(x+1)=nx+n,
联立方程组,得:,
∴x2﹣(3+n)x﹣4﹣n=0,
∴xQ=4+n,yQ=n2+5,
即Q(n+4,n2+5),
∵直线PQ过点E(4,2),
∴kEP=kEQ,
∴=,
即=,
∴mn2+3m=m2n+3n,
mn(m﹣n)=3(m﹣n),
∵P、Q不重合,即m≠n,
∴mn=3,
∴OM•ON=3为定值.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2021/10/24 11:01:53;用户:教师17;邮箱:zybang17@xyh.com;学号:38915552
人教版九年级上册数学期中测试卷(附答案): 这是一份人教版九年级上册数学期中测试卷(附答案),共9页。
【期中模拟】湘教版数学九年级上册--期中测试卷(较易)(含答案): 这是一份【期中模拟】湘教版数学九年级上册--期中测试卷(较易)(含答案),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
【期中模拟】湘教版数学九年级上册--期中测试卷(困难)(含答案): 这是一份【期中模拟】湘教版数学九年级上册--期中测试卷(困难)(含答案),共35页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












