人教版六年级下册比和比例复习ppt课件

这是一份人教版六年级下册比和比例复习ppt课件，共22页。PPT课件主要包含了表示两个数相除，化简比的依据，解比例的依据，分数线，分数值，一个数，被除数，一种运算，表示两个数相除的关系，用前项除以后项等内容，欢迎下载使用。
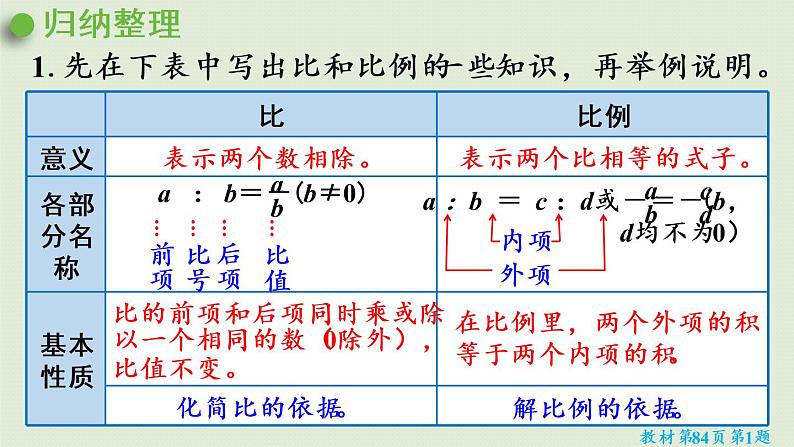
1.先在下表中写出比和比例的一些知识，再举例说明。
表示两个比相等的式子。
比的前项和后项同时乘或除以一个相同的数（0除外），比值不变。
在比例里，两个外项的积等于两个内项的积。
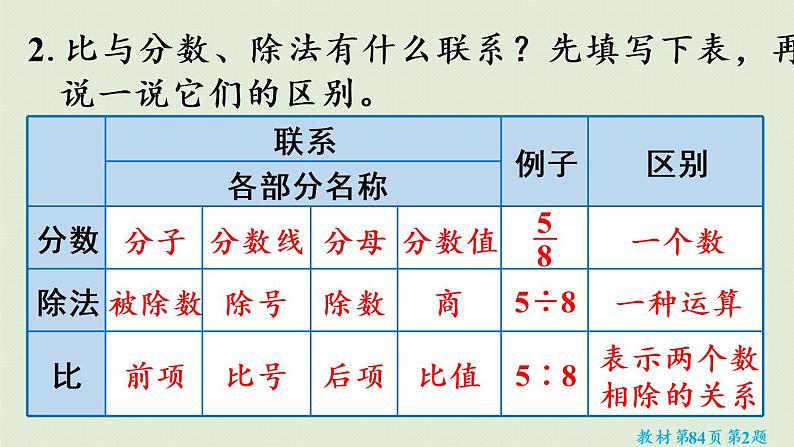
2.比与分数、除法有什么联系？先填写下表，再说一说它们的区别。
3.比的基本性质、分数的基本性质、商不变的规律之间有什么联系？
比的前项和后项同时乘或除以相同的数（0除外），比值不变。
三者只是各部分名称不同，实质是一样的，蕴含着相同的道理。
分数的分子和分母同时乘或除以相同的数（0除外），分数的大小不变。
被除数和除数同时乘或除以相同的数（0除外），商不变。
4.求比值和化简比之间有什么联系？
可以利用求比值的方法来化简比，也可以先化简比，再求比值。
方法一：根据比的基本性质化简。方法二：先求比值，用最简分数表示商，再改写成比。
结果是一个数（整数、分数或小数）。
结果是一个最简整数比。
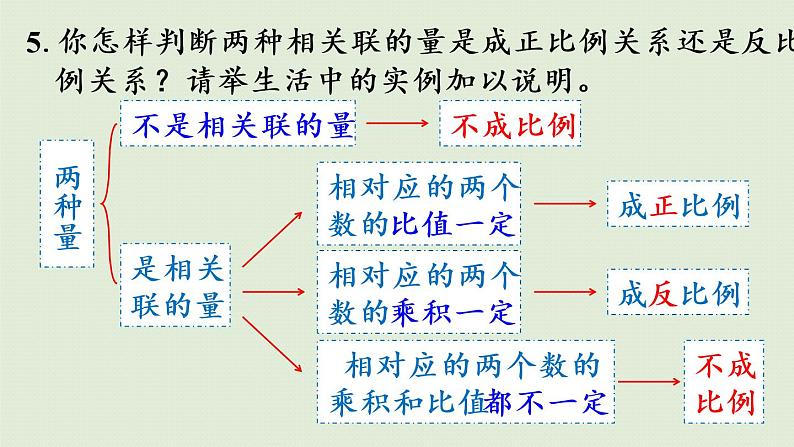
5.你怎样判断两种相关联的量是成正比例关系还是反比例关系？请举生活中的实例加以说明。
相对应的两个数的比值一定
相对应的两个数的乘积一定
相对应的两个数的乘积和比值都不一定
分数法：把比转化为分数，用分数乘法解答。
怎样解决按比分配问题？
份数法（归一法）：把比看作各部分分得的份数，先求出总份数，然后用“总量÷总份数”求出每份的量（归一），再用“每份的量×各部分量所对应的份数”求出各部分的量。
列比例式解答：先设未知量为x，然后根据题中“已知比等于相对应的量的比”作为等量关系，列出含有x的比例式，再求出x的值。
找等量关系：如果判断成正(反)比例关系，则按“等比值”（“等积”）找等量关系。
说一说解正比例、反比例应用题的基本步骤。
分析数量关系：依据相关联的量之间的数量关系式，判断它们成什么比例关系。
列比例式解比例检验，作答
（1）人的头发的寿命约为3年，睫毛的寿命约为4个月。睫毛与头发的寿命比是（ ）。
（2）两个正方形的边长比是4∶1，它们的周长比是（ ），面积比是（ ）。
正方形的周长＝边长×4
周长比：（4×4）∶（1×4）＝4∶1
正方形的面积＝边长×边长
面积比：（4×4）∶（1×1）＝16∶1
（3）一个三角形三个内角的度数比是1∶4∶5，这个三角形是（ ）。
可以根据比的基本性质化简比。
也可以用求比值的方法化简比。
（5）如果6a＝5b＝3c，那么a∶b＝（ ），a∶b∶c＝（ ）。
因为6a＝5b，所以6a÷6b＝5b÷6b，可得a∶b＝5∶6；
同理，可得b∶c＝3∶5，根据比例的基本性质，可得b∶c＝6∶10；所以a∶b∶c＝5∶6∶10。
（2） — ＝ ——
解：3.25x＝6.5×4
3.25x÷3.25＝26÷3.25
3.一支工程队铺一段铁路，原计划每天铺3.2千米，实际每天比原计划多铺25%，实际铺完这段铁路用了12天，原计划用多少天才能铺完？
解：设原计划用x天才能铺完。 3.2x＝3.2×（1＋25%）×12
答：原计划用15天才能铺完。
4.某造纸厂每小时造纸1.5吨，2小时、3小时……各造纸多少吨？
（1）把下表填写完整。
1.5×3＝4.5（吨）
（2）根据表中的数据，在右图中描出造纸时间和造纸吨数对应的点，再把它们连起来。
（3）造纸吨数与造纸时间成正比例关系吗？为什么？
造纸吨数与造纸时间成正比例关系。因为“造纸吨数÷造纸时间＝每小时造纸吨数”，每小时造纸吨数一定。
5.在一幅比例尺是1∶5000000的地图上，量得两地之间的距离是2.4厘米。如果将这两地画在比例尺是1∶15000000的地图上，两地之间的图上距离是多少厘米？