初中华师大版第27章 圆综合与测试习题课件ppt

这是一份初中华师大版第27章 圆综合与测试习题课件ppt，共33页。PPT课件主要包含了答案呈现，AC＝AE，1AD＝BC，2AE＝CE等内容，欢迎下载使用。
如图，在以原点为圆心，2为半径的⊙O上有一点C，∠COA＝45°，则点C的坐标为(　　)
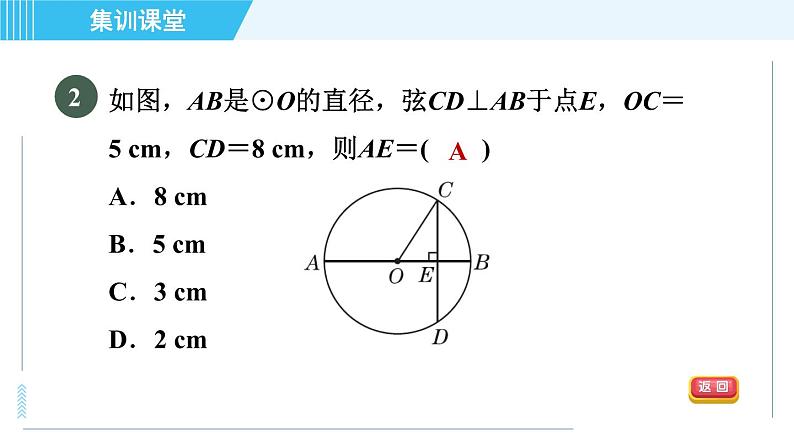
如图，AB是⊙O的直径，弦CD⊥AB于点E，OC＝5 cm，CD＝8 cm，则AE＝(　　)A．8 cm B．5 cm C．3 cm D．2 cm
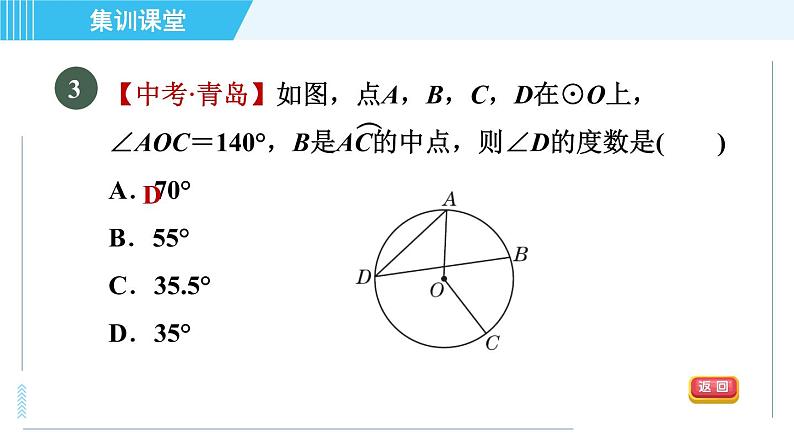
【中考·青岛】如图，点A，B，C，D在⊙O上，∠AOC＝140°，B是AC的中点，则∠D的度数是(　　)A．70° B．55° C．35.5° D．35°
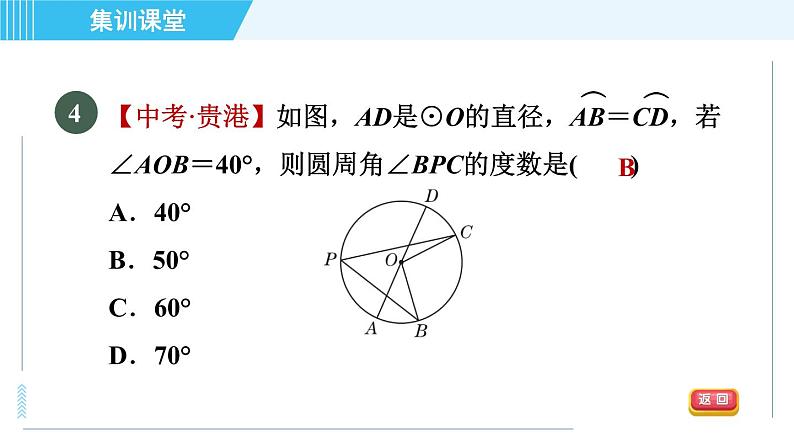
【中考·贵港】如图，AD是⊙O的直径，AB＝CD，若∠AOB＝40°，则圆周角∠BPC的度数是(　　)A．40° B．50° C．60° D．70°
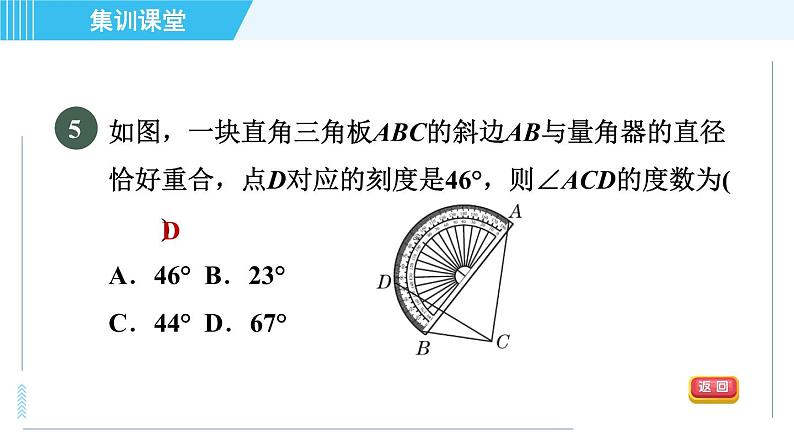
如图，一块直角三角板ABC的斜边AB与量角器的直径恰好重合，点D对应的刻度是46°，则∠ACD的度数为(　　)A．46° B．23° C．44° D．67°
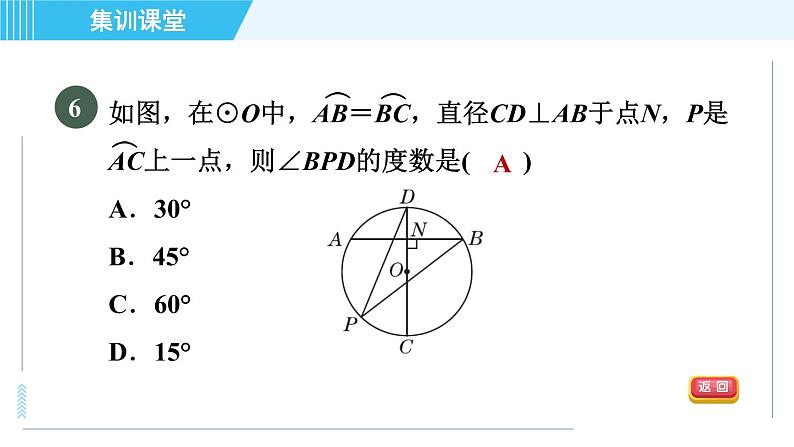
如图，在⊙O中，AB＝BC，直径CD⊥AB于点N，P是AC上一点，则∠BPD的度数是(　　)A．30° B．45° C．60° D．15°
【2021·吉林】如图，四边形ABCD内接于⊙O，点P为边AD上任意一点(点P不与点A，D重合)连接CP.若∠B＝120°，则∠APC的度数可能为(　　)A．30° B．45° C．50° D．65°
【2021·淄博】“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺．问：径几何？”用现在的几何语言表达即：如图，CD为⊙O的直径，弦AB⊥CD，垂足为点E，CE＝1寸，AB＝10寸，则直径CD的长度是(　　)A.12寸 B．24寸C．13寸 D．26寸
【点拨】如图，连接OA. ∵AB⊥CD，AB＝10寸，∴AE＝BE＝5寸．设⊙O的半径OA的长为x寸，则OC＝OD＝x寸．∵CE＝1寸，∴OE＝(x－1)寸．在直角三角形AOE中，根据勾股定理，得x2－(x－1)2＝52，化简得：x2－x2＋2x－1＝25，即2x＝26，∴CD＝26寸．
已知⊙O中最长的弦是12 cm，弦AB＝6 cm，则∠AOB＝________.
【中考·泉州】如图，在⊙O的内接四边形ABCD中，点E在DC的延长线上．若∠A＝50°，则∠BCE＝________.
如图，在平面直角坐标系中，点O为坐标原点，点P在第一象限，⊙P过原点，且与x轴、y轴分别交于点A，B，点A的坐标为(6，0)，⊙P的直径为10，则点B的坐标为________.
如图，AB，CD是⊙O的直径，弦DE∥AB，则AC与AE的大小关系是____________.
如图，点A，B，C在⊙O上，AE是⊙O的直径，AD⊥BC，垂足为点D，若∠DAC＝20°，则∠BAE＝________.
【中考·南宁改编】如图，AB是⊙O的直径，AB＝8，点M是⊙O上的点，∠MAB＝20°，N是MB的中点，P是直径AB上的一动点，则PM＋PN的最小值为________.
(10分)【教材P46习题T9改编】【中考·自贡】如图，⊙O中，弦AB与CD相交于点E，AB＝CD，连结AD，BC.求证：
证明：∵AB＝CD，∴AB＝CD，即AD＋AC＝BC＋AC，∴AD＝BC.
证明∵AD＝BC，∴AD＝BC.∵∠ADE＝∠CBE，∠DAE＝∠BCE，∴△ADE≌△CBE，∴AE＝CE.
(12分)如图，在Rt△ABC中，∠ABC＝90°，点M是AC的中点，以AB为直径作⊙O分别交AC，BM于点D，E.
(1)求证：MD＝ME；
证明：∵在Rt△ABC中，点M是AC的中点，∴MA＝MB，∴∠A＝∠MBA.连结DE，则四边形ABED是⊙O的内接四边形，∴∠ADE＋∠ABE＝180°.∵∠ADE＋∠MDE＝180°，∴∠MDE＝∠MBA.同理可得∠MED＝∠A，∴∠MDE＝∠MED，∴MD＝ME.
证明：∵∠C＝30°，∴∠A＝60°，∴∠ABM＝60°.∵OB＝OE，∴△OBE为等边三角形，∴∠BOE＝60°，∴∠BOE＝∠A，∴OE∥AC.同理可得OD∥BM，∴四边形ODME为平行四边形．又∵OD＝OE，∴四边形ODME是菱形．
(2)连结OD，OE，当∠C＝30°时，求证：四边形ODME是菱形.
(12分)如图，AB是⊙O的一条弦，OD⊥AB，垂足为C，OD交⊙O于点D，点E在⊙O上.
(1)若∠AOD＝54°，求∠DEB的度数；
(2)若CD＝2，AB＝8，求⊙O的半径.
(12分)【2021·荆门】如图，在△ABC中，∠BAC＝90°，点E在BC边上，过A，C，E三点的⊙O交AB边于另一点F，且F是AE的中点，AD是⊙O的一条直径，连接DE并延长交AB边于M点.
证明：如图，连接DF.∵∠BAC＝90°，∴FC是⊙O的直径．∵F是AE的中点，∴AF＝EF.∴∠ADF＝∠EDF.
(1)求证：四边形CDMF为平行四边形；
∵OF＝OD，∴∠ADF＝∠OFD.∴∠OFD＝∠EDF.∴FC∥DM.∵OA＝OD，OF＝OC，∠BAC＝90°，∴四边形AFDC为矩形．∴AF∥CD.∴四边形CDMF为平行四边形．
解：如图，连接EF.∵四边形AFDC为矩形，四边形CDMF为平行四边形，F是AE的中点，∴CD＝AF＝FM＝EF.