2022年中考数学一轮导向练习《锐角三角函数》（含答案）

这是一份2022年中考数学一轮导向练习《锐角三角函数》（含答案），共4页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题
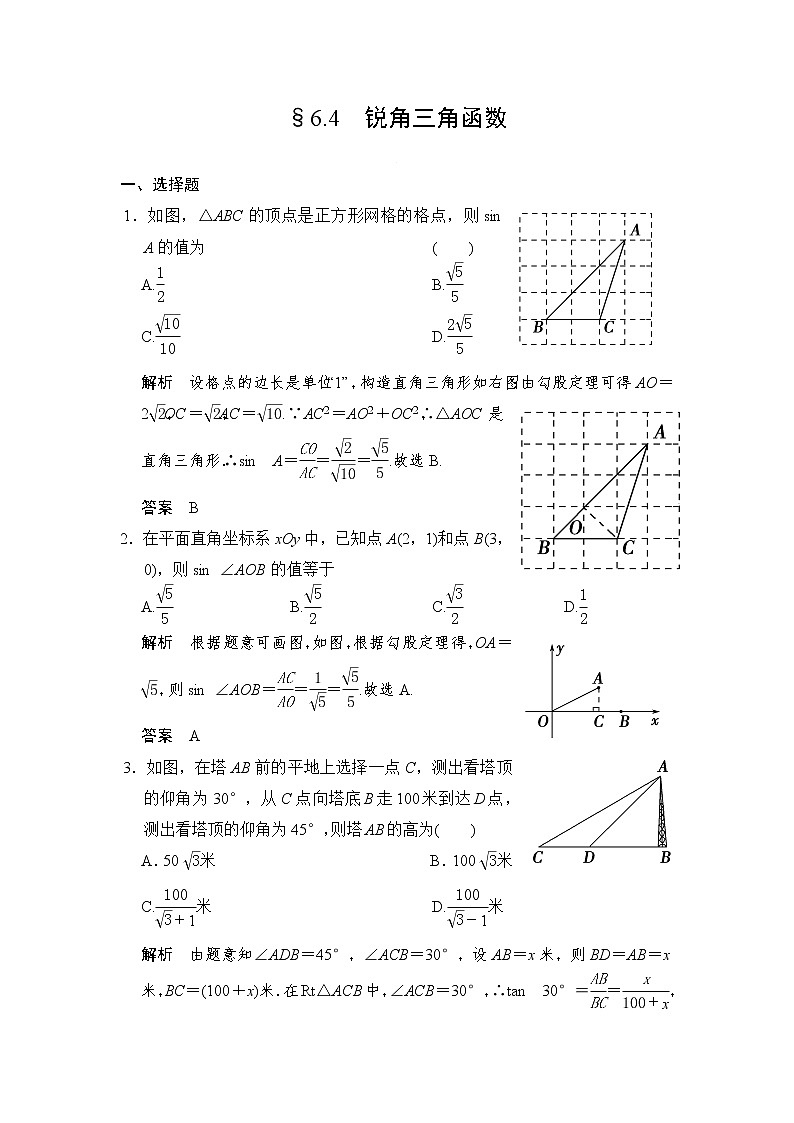
1．如图，△ABC的顶点是正方形网格的格点，则sin A的值为( )
A.eq \f(1,2) B.eq \f(\r(5),5)
C.eq \f(\r(10),10) D.eq \f(2\r(5),5)
解析 设格点的边长是单位“1”，构造直角三角形如右图：由勾股定理可得AO＝2eq \r(2)，OC＝eq \r(2)，AC＝eq \r(10).∵AC2＝AO2＋OC2，∴△AOC是直角三角形．∴sin A＝eq \f(CO,AC)＝eq \f(\r(2),\r(10))＝eq \f(\r(5),5).故选B.
答案 B
2．在平面直角坐标系xOy中，已知点A(2，1)和点B(3，0)，则sin ∠AOB的值等于( )
A.eq \f(\r(5),5) B.eq \f(\r(5),2) C.eq \f(\r(3),2) D.eq \f(1,2)
解析 根据题意可画图，如图，根据勾股定理得，OA＝eq \r(5)，则sin ∠AOB＝eq \f(AC,AO)＝eq \f(1,\r(5))＝eq \f(\r(5),5).故选A.
答案 A
3．如图，在塔AB前的平地上选择一点C，测出看塔顶的仰角为30°，从C点向塔底B走100米到达D点，测出看塔顶的仰角为45°，则塔AB的高为( )
A．50eq \r(3)米 B．100eq \r(3)米
C.eq \f(100,\r(3)＋1)米 D.eq \f(100,\r(3)－1)米
解析 由题意知∠ADB＝45°，∠ACB＝30°，设AB＝x米，则BD＝AB＝x米，BC＝(100＋x)米．在Rt△ACB中，∠ACB＝30°，∴tan 30°＝eq \f(AB,BC)＝eq \f(x,100＋x)，即eq \f(x,100＋x)＝eq \f(\r(3),3).解得x＝eq \f(100,\r(3)－1).故选D.
答案 D
4．学校大门出口处有一自动感应栏杆，点A是栏杆转动的支点，当车辆经过时，栏杆AE会自动升起，某天早上，栏杆发生故障，在某个位置突然卡住，这时测得栏杆升起的角度∠BAE＝127°，已知AB⊥BC，支架AB高1.2米，大门BC打开的宽度为2米，以下哪辆车可以通过(栏杆宽度，汽车反光镜忽略不计)(参考数据：sin 37°≈0.60，cs 37°≈0.80，tan 37°≈0.75.车辆尺寸：长×宽×高)( )
A．宝马Z4(4 200 mm×1 800 mm×1 360 mm)
B．奇瑞QQ(4 000 mm×1 600 mm×1 520 mm)
C．大众朗逸(4 600 mm×1 700 mm×1 400 mm)
D．奥迪A4(4 700 mm×1 800 mm×1 400 mm)
解析 如图，过点A作BC的平行线AG，过点N作NQ⊥BC于Q，交AG于点R，则∠BAG＝90°.∵∠BAE＝127°，∠BAG＝90°，∴∠EAG＝∠EAB－∠BAG＝37°.在△NAR中，∠ARN＝90°，∠EAG＝37°，当车宽为1.8 m时，则GR＝1.8 m，故AR＝2－1.8＝0.2(m)，∴NR＝ARtan 37°＝0.2×0.75＝0.15(m)，∴NQ＝1.2＋0.15＝1.35＜1.36，∴宝马Z4(4 200 mm×1 800 mm×1 360 mm)无法通过，奥迪A4(4 700 mm×1 800 mm×1 400 mm)无法通过，故此选项A，D不合题意；当车宽为1.6 m时，则GR＝1.6 m，故AR＝2－1.6＝0.4(m)，∴NR＝ARtan 37°＝0.4×0.75＝0.3(m)，∴NQ＝1.2＋0.3＝1.5＜1.52，∴奇瑞QQ(4 000 mm×1 600 mm×1 520 mm)无法通过，故此选项不合题意；当车宽为1.7 m时，则GR＝1.7 m，故AR＝2－1.7＝0.3(m)，∴NR＝ARtan 37°＝0.3×0.75＝0.225(m)，∴NQ＝1.2＋0.225 ＝1.425 ＞1.4，∴大众朗逸(4 600 mm×1 700 mm×1 400 mm)可以通过，故此选项符合题意．故选C.
答案 C
二、填空题
5．如图，已知tan O＝eq \f(4,3)，点P在边OA上，OP＝5，点M，N在边OB上，PM＝PN，如果MN＝2，那么PM＝________．
解析 过P作PD⊥OB，交OB于点D，∵tan O＝eq \f(PD,OD)＝eq \f(4,3)，∴设PD＝4x，则OD＝3x.
∵OP＝5，由勾股定理得：(3x)2＋(4x)2＝52，
∴x＝1，∴PD＝4.
∵PM＝PN，PD⊥OB，MN＝2
∴MD＝ND＝eq \f(1,2)MN＝1.
在Rt△PMD中，由勾股定理得：
PM＝eq \r(MD2＋PD2)＝eq \r(17)，
答案 eq \r(17)
6．如图，为了测量电线杆AB的高度，小明将测角仪放在与电线杆的水平距离为9 m的D处，若测角仪CD的高度为1.5 m，在C处测得电线杆顶端A的仰角为36°，则电线杆AB的高度约为________ m．(精确到0.1 m)(参考数据：sin 36°≈0.59，cs 36°≈0.81，tan 36°≈0.73)
解析 作CE⊥AB于E，在Rt△ACE中，tan 36°＝eq \f(AE,CE)，AE＝CE·tan 36°≈9×0.73＝6.57，AB＝AE＋BE≈6.57＋1.5＝8.07≈8.1.故答案填：8.1.
答案 8.1
三、解答题
7．如图，已知灯塔A的周围7海里的范围内有暗礁，一艘渔轮在B处测得灯塔A在北偏东60°的方向，向正东航行8海里到C处后，又测得该灯塔在北偏东30°方向，渔轮不改变航向，继续向东航行，有没有触礁危险？请通过计算说明理由．(参考数据eq \r(3)≈1.732)
解 作AD⊥BC交BC的延长线于D.
设AD＝x.
在Rt△ACD中，∠CAD＝30°，
∴CD＝x·tan 30°＝eq \f(\r(3),3)x.
在Rt△ABD中，∠ABD＝30°，
∴BD＝eq \r(3)x.
∵BC＝8，∴eq \r(3)x－eq \f(\r(3),3)x＝8.
解得x＝4eq \r(3)≈6.928.
∵6.928海里