2021届高考数学二轮复习常考题型大通关（新高考）选择题：导数及其应用

这是一份2021届高考数学二轮复习常考题型大通关（新高考）选择题：导数及其应用，共8页。试卷主要包含了已知曲线在点处的切线方程为，则，若，则函数在区间上恰好有等内容，欢迎下载使用。
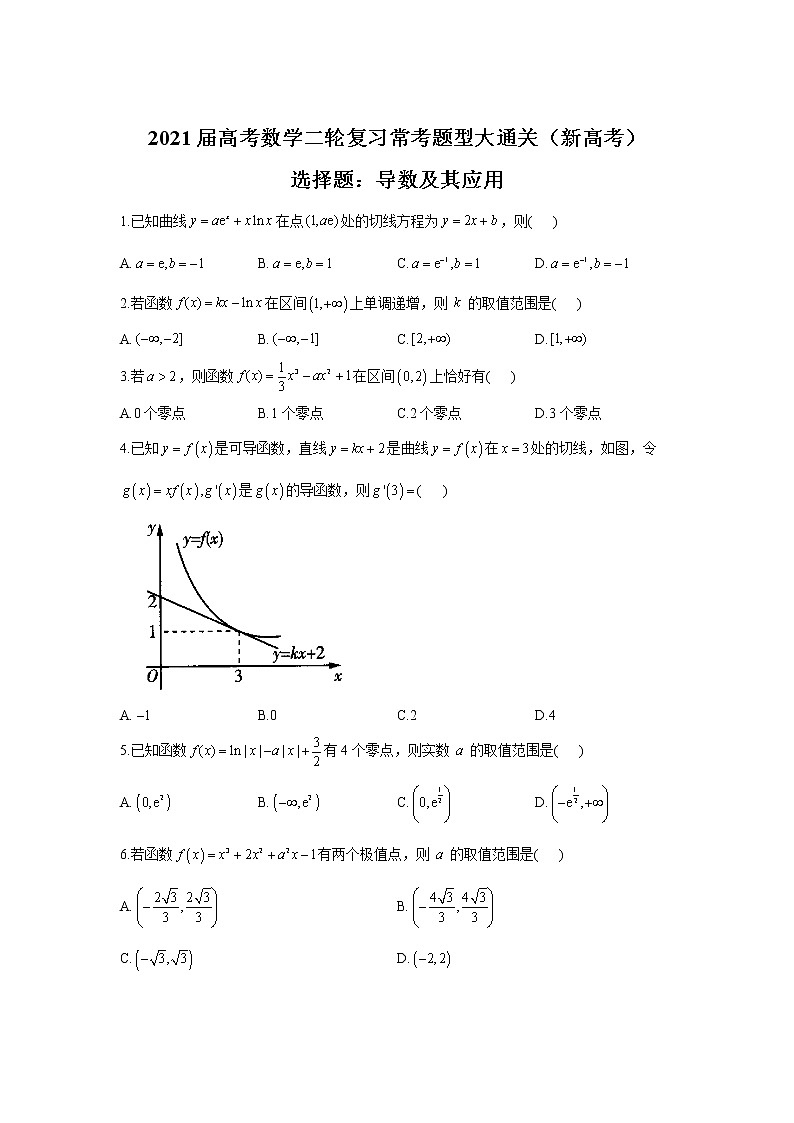
 2021届高考数学二轮复习常考题型大通关（新高考）选择题：导数及其应用1.已知曲线在点处的切线方程为，则(   )A. B. C. D.2.若函数在区间上单调递增，则的取值范围是(   )A. B. C. D.3.若，则函数在区间上恰好有(   )A.0个零点 B.1个零点 C.2个零点 D.3个零点4.已知是可导函数，直线是曲线在处的切线，如图，令是的导函数，则(   )A. B.0 C.2 D.45.已知函数有4个零点，则实数的取值范围是(   )A. B. C. D.6.若函数有两个极值点，则的取值范围是(   )A.  B.C.  D.7.已知奇函数是定义在上的连续可导函数，其导函数是，当时，恒成立，则下列不等关系中一定正确的是(   )A.  B. C.  D.8.已知函数，若存在，使得关于的不等式恒成立，则的取值范围为(   )A. B. C. D.9.已知函数有两个不同的极值点，若不等式恒成立，则实数的取值范围是(   )A. B. C. D.10.定义在上的偶函数的导函数为，且当时，，则(   )A.  B.C.  D.11.已知在上连续可导，为其导函数，且，则(   )A. B. C.0 D.12.已知函数在上单调递增，则实数的取值范围是(   )A.  B.C.  D.13.已知函数，则不等式的解集是(   )A.  B.C.  D.14.已知，设函数若关于的不等式在上恒成立，则的取值范围为(   )A. B. C. D.15.已知的定义域为为的导函数，且满足，则不等式的解集是(   )A. B. C. D. 
答案以及解析1.答案：D解析：因为，所以，所以曲线在点处的切线方程为，即，所以解得2.答案：D解析：由于，则在区间上单调递增在上恒成立.因为时，，所以，即的取值范围为.3.答案：B解析：，又，当时，，函数单调递减.又在上恰好有1个零点.4.答案：B解析：由题图可知，曲线在处切线的斜率等于，.，，又由题图可知.5.答案：C解析：函数的定义域为，关于原点对称，函数为偶函数.函数有4个零点，当时，函数有2个零点，即方程有2个根，即曲线与直线有2个交点.如图，当直线为曲线的切线，且经过点时，设切点坐标为，则.直线的方程为，将代入，得，.由图可知，即，故选C.6.答案：A解析：.因为函数有两个极值点，所以有两个不等的实根，则，解得，故选A.7.答案：C解析：构造函数，则当时，，即函数在上单调递减，所以，即，所以，故选C.8.答案：A解析：解法一  当时，，所以.当时，令，因为存在，使得，等价于，所以存在，使得关于的不等式恒成立，等价于恒成立.令，则，所以单调递增，所以，故.当时，因为，所以，所以存在，使得关于的不等式恒成立，等价于恒成立.令，则单调递减，所以，故.综上，得.解法二  ，当时，，所以单调递减，且当趋近于时，趋近于，与不等式恒成立矛盾，舍去；当时，令，得，所以在区间上单调递增，令，得，所以在区间上单调递减，所以存在，使得成立.令，则，所以当时，单调递增；当时，单调递减.所以，故.9.答案：A解析：，设，要使存在两个不同的极值点，则方程有两个不同的根，且，结合，得.，令，则.当时，单调递增，故在上，，所以.10.答案：D解析：根据题意，设，则，又当时，，所以当时，，则函数在上为减函数.由，且为偶函数，知，即为偶函数.由，得，因为为偶函数，所以，所以，故选D.11.答案：C解析：函数，即函数是偶函数，两边对求导数，得.即，则是上的奇函数，则，即，则.故选C.12.答案：D解析：由题意知，由于在上单调递增，则在上恒成立，即在上恒成立.当时，，则有，解得或.故选D.13.答案：D解析：函数的定义域为，其导数为.令，得.因为，所以.当时，单调递减；当时，单调递增.又，所以的解集为，故选D.快解  可利用排除法，，排除A，C；，排除B.故选D.14.答案：C解析：由题意知当时，恒成立，即恒成立.当时，在上单调递减，成立；当时，在上单调递减，在上单调递增，，解得，故.所以.当时，恒成立，即在上恒成立.令，则，当时，单调递增；当时，单调递减，易知为函数在上唯一的极小值点，也是最小值点，故，所以.综上可知，的取值范围是.故选C.15.答案：B解析：构造函数，则，所以函数的图像在上单调递减.又因为，所以，所以，解得或(舍).所以不等式的解集是.故选B.