2021届高考数学二轮复习常考题型大通关（新高考）选择题：三角函数

这是一份2021届高考数学二轮复习常考题型大通关（新高考）选择题：三角函数，共7页。试卷主要包含了已知，则，已知，且，则，函数的最小正周期为等内容，欢迎下载使用。
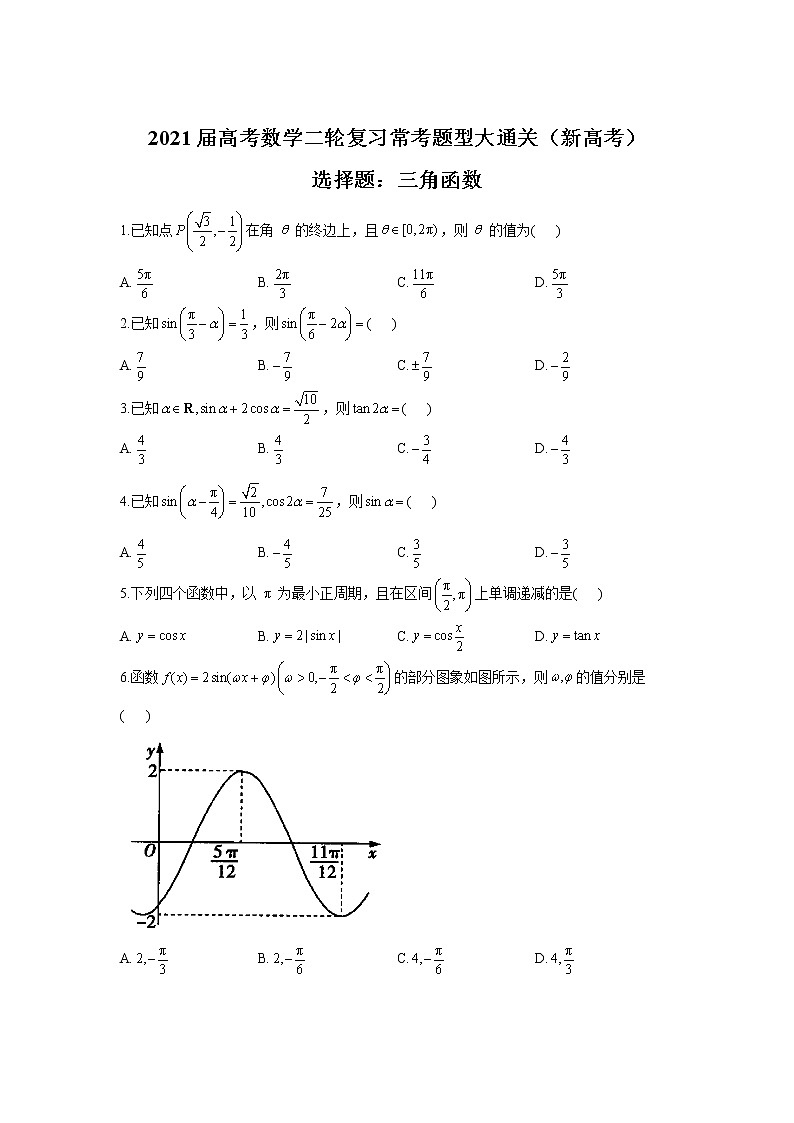
 2021届高考数学二轮复习常考题型大通关（新高考）选择题：三角函数1.已知点在角的终边上，且，则的值为(   )A. B. C. D.2.已知，则(   )A. B. C. D.3.已知，则(   )A. B. C. D.4.已知，则(   )A. B. C. D.5.下列四个函数中，以为最小正周期，且在区间上单调递减的是(   )A. B. C. D.6.函数的部分图象如图所示，则的值分别是(   )A. B. C. D.7.已知函数，将图象上各点的横坐标伸长为原来的2倍(纵坐标不变)，再向左平移个单位长度，得到函数的图象.已知分别在处取得最大值和最小值，则的最小值为(   )A. B. C. D.8.设函数在的图象大致如图，则的最小正周期为(   )A. B. C. D.9.已知，且，则(   )A. B. C. D.10.函数的最小正周期为（   ）A．      B．  C．       D．11.将曲线向右平移个单位长度后得到曲线，若函数的图象关于轴对称，则等于(   )A. B. C. D.12.已知函数，其中为实数，若对任意的恒成立，且，则的单调递减区间是(   )A.   B.C. D.13.与30°角终边相同的角的集合是(   )A. B.C.  D.14.函数的部分图象如图所示.为了得到这个函数的图象，只要将的图象上所有的点(   )A.向左平移个单位长度，再把各点的横坐标缩短为原来的，纵坐标不变B.向左平移个单位长度，再把各点的横坐标伸长为原来的2倍，纵坐标不变C.向左平移个单位长度，再把各点的横坐标缩短为原来的，纵坐标不变D.向左平移个单位长度，再把各点的横坐标伸长为原来的2倍，纵坐标不变15.关于函数有下述四个结论：①是偶函数②在区间单调递增③在有4个零点④的最大值为2其中所有正确结论的编号是(   )A.①②④ B.②④ C.①④ D.①③


 
答案以及解析1.答案：C解析：因为点在第四象限，，所以.根据三角函数的定义可知，所以，故选C.2.答案：B解析：因为，所以.3.答案：C解析：因为，所以，整理得，则，所以.4.答案：C解析：由得.①，由得，所以.②，由①②可得.③，由①③可得.5.答案：B解析：对于A，的最小正周期为，所以A不符合题意；对于B，结合函数图象可知的最小正周期为，且在上单调递减，所以B符合题意；对于C，的最小正周期为，所以C不符合题意；对于D，的最小正周期为，且在区间上单调递增，所以D不符合题意.故选B.6.答案：A解析：由题中图象可知(为的最小正周期)，.又函数的图象经过点，，，又，故选A.7.答案：B解析：因为，所以，所以，即，，即，则，当时，取得最小值，故选B.8.答案：C解析：通解  由题图知，，解得.设的最小正周期为，易知，，当且仅当时，符合题意，此时.故选C.秒解  由题图知，且，解得的最小正周期.故选C.9.答案：A解析：，，解得(舍去)或..故选A.10.答案：C解析：， 则函数是偶函数， 函数的最小正周期，即是最小正周期为的偶函数，故选：C.11.答案：D解析：曲线向右平移个单位长度后得到曲线，则，若函数的图象关于轴对称，则，则，又，所以.故选D.12.答案：C解析：由题意可得函数的图象关于直线对称，故有，即.又，所以，故.令，解得，故函数的单调递减区间为.13.答案：D解析：与30°角终边相同的角表示为，化为弧度制为.14.答案：A解析：观察题中图象知，，所以，即.将代入得，所以，又，得，所以，结合三角函数的图象变换可知选A.15.答案：C解析：通解  为偶函数，故①正确；当时，在单调递减，故②不正确；在的图象如图所示，由图可知函数在只有3个零点，故③不正确；与的最大值都为1且可以同时取到，可以取到最大值2，故④正确.综上，正确结论的序号是①④.故选C.优解  为偶函数，故①正确，排除B；当时，在单调递减，故②不正确，排除A；与的最大值都为1且可以同时取到，的最大值为2，故④正确.故选C.