初中数学青岛版九年级下册6.4随机现象的变化趋势精品课堂检测

这是一份初中数学青岛版九年级下册6.4随机现象的变化趋势精品课堂检测，共27页。试卷主要包含了4随机现象的变化趋势同步练习，0分），5浓度和空气质量AQI的统计图，073，0，5千克的学生大约有多少人？，【答案】C，4，，【答案】D等内容，欢迎下载使用。

青岛版初中数学九年级下册
注意：本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题，所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题，所有答案必须填在答题卷的相应位置。答案写在试卷上均无效，不予记分。
一、选择题（本大题共12小题，共36.0分）
2020年是全面打赢脱贫攻坚战的收官之年，全国832个贫困县全部脱贫摘帽．经2020年精准扶贫后，某贫困村的经济收入增加了一倍．为更好地了解该村的经济收入变化情况，统计了该村精准扶贫前后的经济收入构成比例，得到如下统计图：则下面结论中不正确的是( )
A. 精准扶贫后，种植收入减少
B. 精准扶贫后，其他收入增加了一倍以上
C. 精准扶贫后，养殖收入增加了一倍
D. 精准扶贫后，养殖收入与第三产业收入的总和超过了经济收入的一半
某学校为了加强学生的安全意识，组织学生观看了纪实片《孩子，请不要私自下水》，并对部分学生进行调查．根据下面两幅不完整的统计图可以求出，在这次调查中被调查的学生有( )
A. 400名B. 380名C. 350名D. 300名
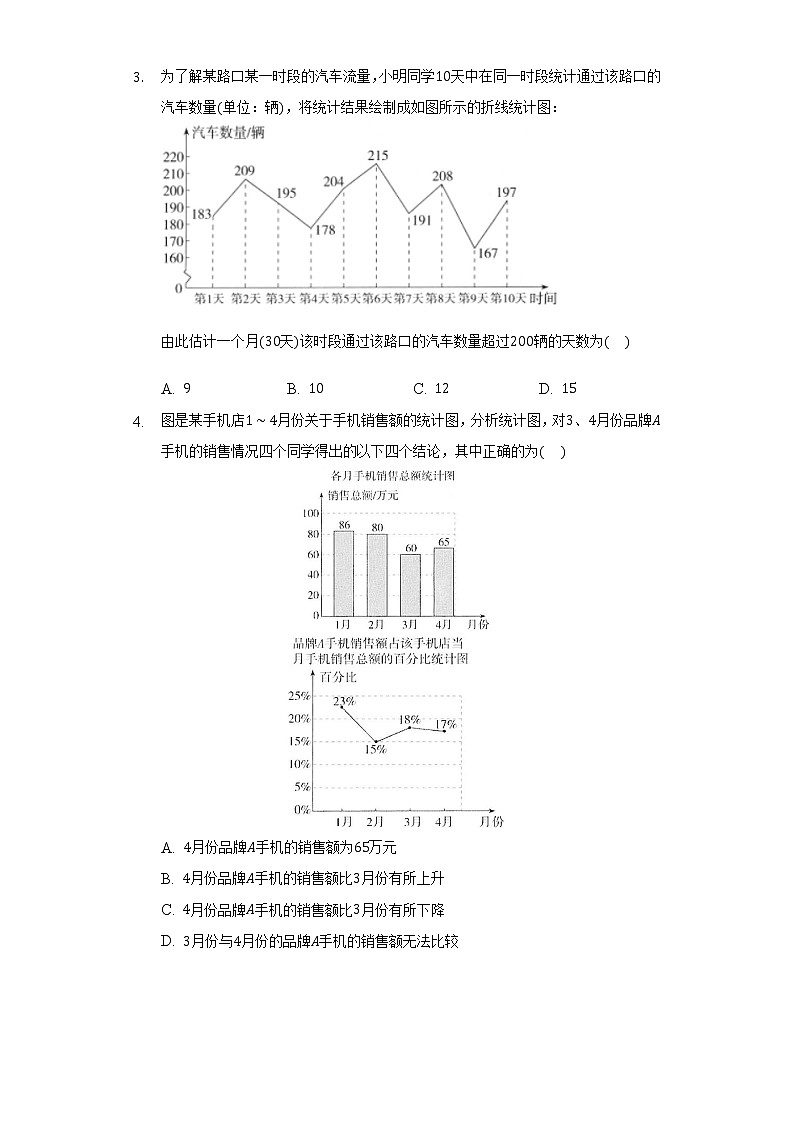
为了解某路口某一时段的汽车流量，小明同学10天中在同一时段统计通过该路口的汽车数量(单位：辆)，将统计结果绘制成如图所示的折线统计图：
由此估计一个月(30天)该时段通过该路口的汽车数量超过200辆的天数为( )
A. 9B. 10C. 12D. 15
图是某手机店1∼4月份关于手机销售额的统计图，分析统计图，对3、4月份品牌A手机的销售情况四个同学得出的以下四个结论，其中正确的为( )
A. 4月份品牌A手机的销售额为65万元
B. 4月份品牌A手机的销售额比3月份有所上升
C. 4月份品牌A手机的销售额比3月份有所下降
D. 3月份与4月份的品牌A手机的销售额无法比较
根据李飞与刘亮射击训练的成绩绘制了如图所示的折线统计图．
根据图所提供的信息，若要推荐一位成绩较稳定的选手去参赛，应推荐( )
A. 李飞或刘亮B. 李飞C. 刘亮D. 无法确定
某校实施课程改革，为初三学生设置了Ａ，B，Ｃ，D，E，F共六门不同的拓展性课程，现随机抽取若干学生进行了“我最想选的一门课”调查，并将调查结果绘制成如图的统计图表(不完整)：
根据图表提供的信息，下列结论错误的是( )
A. 这次被调查的学生人数为200
B. 扇形统计图中E部分扇形的圆心角为72°
C. 被调查的学生中最想选D的有55人
D. 被调查的学生中最想选F的人数为35
为积极响应创建“全国卫生城市”的号召，某校1500名学生参加了卫生知识竞赛，成绩记为A，B，C，D四等，从中随机抽取了部分成绩进行统计，绘制成如图两幅不完整的统计图，根据图中信息，以下说法不正确的是( )
A. 样本容量是200
B. D等所对应的扇形圆心角为15°
C. 样本中C等所占百分比是10%
D. 估计全校学生成绩为A等的大约有900人
“救死扶伤”是我国的传统美德，某媒体就“老人摔倒该不该扶”进行了调查，将得到的数据统计分析后绘制成如图所示的扇形统计图．根据统计图判断下列说法，错误的一项是( )
A. 认为依情况而定的占27%
B. 认为该扶的在统计图中所对应的圆心角是234°
C. 认为不该扶的占8%
D. 认为该扶的占92%
随着长株潭一体化进程不断推进，湘潭在交通方面越来越让人期待．将要实施的“两干一轨”项目中的“一轨”，是将长沙市地铁3号线南延至湘潭北站，往返长潭两地又将多“地铁”这一选择．为了解人们选择交通工具的意愿，随机抽取了部分市民进行调查，并根据调查结果绘制如下统计图，关于交通工具选择的人数数据，以下结论正确的是( )
A. 平均数是8B. 众数是11C. 中位数是2D. 极差是10
如图为2021年第一季度中国工程机械出口额TOP10国家的相关数据(同比增速是指相对于2020年第一季度出口额的增长率)，下列说法正确的是( )
A. 对10个国家出口额的中位数是26201万美元
B. 对印度尼西亚的出口额比去年同期减少
C. 去年同期对日本的出口额小于对俄罗斯联邦的出口额
D. 出口额同比增速中，对美国的增速最快
某文具商店共有单价分别为10元、15元和20元的三种文具盒出售，该商店统计了今年3月份这三种文具盒的销售情况，并绘制如图所示的统计图.你认为这个商店4月份购进这三种文具盒的比例较为合理的是( )
A. 1:2:3B. 2: 1: 3C. 3:5:12D. 5:12:3
近年来国内生产总值年增长率的变化情况如图，从图上看，下列结论中不正确的是( )
A. 2015年～2019年，国内生产总值年增长率逐年减少
B. 2020年，国内生产总值的年增长率开始回升
C. 这7年中，每年的国内生产总值不断增长
D. 这7年中，每年的国内生产总值有增有减
二、填空题（本大题共5小题，共15.0分）
为最大程度减少因疫情延迟开学带来的影响，实现“离校不离教、停课不停学”，我市全面开展了形式多样的“线上教学”活动.为了解教学效果，某校对“线上教学”的满意度进行了抽样调查，将抽样调查结果进行统计并绘制成如图所示的两幅不完整的统计图.请结合图中所给的信息计算，表示“非常满意”和“满意”的总人数为 ．
某学校在“你最喜爱的课外活动项目”调查中，随机调查了若干名学生(每名学生只选一个活动项目)，并根据调查结果绘制了如图所示的扇形统计图.已知选最喜爱“体操”的学生有9人，则最喜爱“3D打印”的学生人数为 ．
七年级(1)班有40名学生，在期末体育考试中，优秀的有18人，在扇形统计图中，代表体育优秀扇形的圆心角是______．
如图是某地2月18日到23日PM2.5浓度和空气质量AQI的统计图(当AQI不大于100时称空气质量为“优良”).由图可得下列说法：①18日的PM2.5浓度最低；②21日的PM2.5浓度最高；③这六天中有4天空气质量为“优良”；④空气质量指数AQI与PM2.5浓度有关．其中正确的是______(填序号即可)
某校学生来自甲、乙、丙三个地区，其人数比为2：7：3，如图所示的扇形图表示上述分布情况，则甲地区扇形圆心角∠AOB的度数为______．
三、解答题（本大题共8小题，共64.0分）
A，B两家酒店规模相当，去年下半年的月盈利折线统计图如图所示．
(1)要评价这两家酒店7～12月的月盈利的平均水平，你选择什么统计量？求出这个统计量．
(2)已知A，B两家酒店7～12月的月盈利的方差分别为1.073(平方万元)，0.54(平方万元).根据所给的方差和你在(1)中所求的统计量，结合折线统计图，你认为去年下半年哪家酒店经营状况较好？请简述理由．
某校为了解七年级学生的体重情况，随机抽取了七年级m名学生进行调查，将抽取学生的体重情况绘制如下不完整的频数分布表和扇形统计图．
请根据图表信息回答下列问题：
(1)填空：①m=______，②n=______，③在扇形统计图中，C组所在扇形的圆心角的度数等于______度；
(2)若把每组中各个体重值用这组数据的中间值代替(例如：A组数据中间值为40千克)，则被调查学生的平均体重是多少千克？
(3)如果该校七年级有1000名学生，请估算七年级体重低于47.5千克的学生大约有多少人？
面对今年的新冠疫情，某区所有中学开展了“停课不停学”活动．该区教育主管部门随机调查了一些家长对该活动的态度(A：无所谓；B：赞成；C：反对)，并将调査结果绘制成图①和图②的统计图．请根据图中提供的信息，解答下列问题：

(1)在图①中，C部分所占扇形的圆心角度数为 °；
(2)将图②补充完整；
(3)根据抽样调查结果，估计该区30000名中学生家长中有多少人持赞成态度？
小王和小张是两名射击运动员，在一次测试中，两人各射了10发子弹，其射击成绩如图所示．
(1)请你将表填写完整：
(2)从平均数和中位数相结合来分析谁的成绩好？
(3)从平均数和命中9环以上的次数相结合来分析谁的成绩好？
(4)从折线图上两人射击命中环数的走势相结合来分析谁更有潜力？
2020年初的新冠肺炎疫情对大们的生活造成了较大的影响，为响应教育部下发通知“停课不停学”的倡议，某校准备选用合适的软件对全校学生直播上课，经对直接软件功能进行筛选，学校选定了“钉钉”和“QQ直翻”两款软件进行试用，并组全校师生对这两款软件打分(均为整数，最高5分：最低1分)，随机抽取20名同学和10位教师的打分情况作为样本，分析过程如下．
A.收集数据：20名同学打分情况如下：
B.整理、描述数据：根据学生的打分情况，绘制了如下尚不完整的条形统计图：
C.分析数据：学生打分的平均数、众数、中位数如下表：
D.抽取的10位教师对“钉钉”和“QQ直播”这两款软件打分的平均分分别为4.4分和4分．
请根据以上信息解答下列问题：
(1)请补全条形统计图；
(2)填空：a=______，b=______；
(3)你认为学生对这两款软件评价较高的是______，(填“钉钉”或“QQ直播”)理由是______；
(4)学校决定选择综合平均分高的软件进行教学，其中综合平均分中教师打分占60%，学生打分占40%，请你通过计算分析学校会采用哪款软件进行教学．
图书馆是一个很好的学习平台，某市有关部门统计了最近6个月到图书馆的读者的职业分布情况，并做了下列两个不完整的统计图．
(1)在统计的这段时间内，共有______万人次到图书馆阅读，其中商人占百分比为______%.
(2)将条形统计图补充完整．
(3)5月份到图书馆的读者共有24000人次，根据以上调查结果，估计24000人次中是职工的人次．
为了了解居民的环保意识，社区工作人员在某小区随机抽取了若干名居民开展主题为“打赢蓝天保卫战”的环保知识有奖问答活动，并用得到的数据绘制了如下条形统计图(得分为整数，满分为10分，最低分为6分)．
请根据图中信息，解答下列问题：
(1)本次调查一共抽取了__________名居民；
(2)求本次调查获取的样本数据的平均数、众数和中位数；
(3)社区决定对该小区500名居民开展这项有奖问答活动，得10分者得“一等奖”，请你根据调查结果，帮社区工作人员估计需准备多少份“一等奖”奖品．
为了解学生掌握垃圾分类知识的情况，增强学生环保意识．某学校举行了“垃圾分类人人有责”的知识测试活动，现从该校七、八年级中各随机抽取20名学生的测试成绩(满分10分，6分及6分以上为合格)进行整理、描述和分析，下面给出了部分信息．
七年级20名学生的测试成绩为：7，8，7，9，7，6，5，9，10，9，8，5，8，7，6，7，9，7，10，6．
八年级20名学生的测试成绩条形统计图如图：
七、八年级抽取的学生的测试成绩的平均数、众数、中位数、8分及以上人数所占百分比如下表所示：
根据以上信息，解答下列问题：
(1)直接写出上述表中的a，b，c的值；
(2)根据上述数据，你认为该校七、八年级中哪个年级学生掌握垃极分类知识较好？请说明理由(写出一条理由即可)；
(3)该校七、八年级共1200名学生参加了此次测试活动，估计参加此次测试活动成绩合格的学生人数是多少？
答案和解析
1.【答案】A
【解析】解：设精准扶贫前经济收入为a，精准扶贫后经济收入为2a，
A、种植收入37%×2a−60%a=14%a>0，
则精准扶贫后，种植收入增加，故本选项错误，符合题意；
B、精准扶贫后，其他收入5%×2a=10%a，精准扶贫前，其他收入4%a，
故10%a÷4%a=2.5>2，故本选项正确，不符合题意；
C、精准扶贫后，养殖收入30%×2a=60%a，精准扶贫前，养殖收入30%a，
故60%a÷30%a=2，故本选项正确，不符合题意；
D、精准扶贫后，养殖收入与第三产业收入的总和为(30%+28%)×2a=58%×2a，
经济收入为2a，
故(58%×2a)÷2a=58%>50%，故本选项正确，不符合题意；
故选：A．
设精准扶贫前经济收入为a，精准扶贫后经济收入为2a，根据扇形统计图给出的数据分别对每一项进行分析，即可得出答案．
本题考查的是扇形统计图的应用．读懂统计图，从统计图中得到必要的信息是解决问题的关键．扇形统计图直接反映部分占总体的百分比大小．
2.【答案】A
【解析】解：20÷5%=400人，
故选：A．
从两个统计图可得，“一定会”的有20人，占调查人数的5%，可求出调查人数．
考查扇形统计图、条形统计图的意义和制作方法，从两个统计图中获取数量及数量之间的关系是解决问题的关键，
3.【答案】C
【解析】 解：由题图可知，10天中在同一时段通过该路口的汽车数量超过200辆的有4天，频率为410=0.4，
所以估计一个月(30天)该时段通过该路口的汽车数量超过200辆的天数为30×0.4=12.故选C．
4.【答案】B
【解析】解：3月份品牌A手机的销售额为60×18%=10.8(万元)，4月份品牌A手机的销售额为65×17%=11.05(万元)，
∵11.05>10.8，
∴4月份品牌A手机的销售额比3月份有所上升.故B正确，故选B．
5.【答案】C
【解析】解：李飞的成绩为5、8、9、7、8、9、10、8、9、7，
则李飞成绩的平均数为5+7×2+8×3+9×3+1010=8，
所以李飞成绩的方差为110×[(5−8)2+2×(7−8)2+3×(8−8)2+3×(9−8)2+(10−8)2]=1.8；
刘亮的成绩为7、8、8、9、7、8、8、9、7、9，
则刘亮成绩的平均数为7×3+8×4+9×310=8，
∴刘亮成绩的方差为110×[3×(7−8)2+4×(8−8)2+3×(9−8)2]=0.6，
∵0.6<1.8，
∴应推荐刘亮，
故选：C．
根据折线统计图得出两人射击成绩，再计算出两人成绩的方差，据此即可作出判断．
本题主要考查折线统计图与方差，解题的关键是根据折线统计图得出解题所需数据及方差的计算公式．
6.【答案】C
【解析】
【分析】
本题主要考查扇形统计图，读懂统计图，从统计图中得到必要的信息是解决问题的关键.从扇形图上可以清楚地看出各部分数量和总数量之间的关系．
由B课程的人数及其百分比可得总人数，即可判断A选项;先求得E课程所占百分比，再乘以360°即可判断B;总人数乘以D、F的百分比即可求得人数，从而判断出C、D选项．
【解答】
解：A.由统计表知：喜欢选修课B的人数为30人，
由扇形统计图知：喜欢选修课B的人数占总人数15％，
∴被调查的学生人数为：30÷15％=200(人)，故A正确；
B.由扇形统计图可知，D的圆心角为90°，
∵A部分扇形圆心角为20200×360°=36°，360°×(17.5％+15％+12.5％)=162°，
∴扇形统计图中E的圆心角=360°-162°-90°-36°=72°，
∴选项B正确；
C.被调查的学生中最想选D的有200×90∘360∘=50(人)，故C错误；
D.被调查的学生中最想选F的人数为200×17.5％=35(人)，故D正确．
故选C.
7.【答案】B
【解析】
【分析】
本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
根据条形统计图和扇形统计图提供的数据分别列式计算，再对每一项进行分析即可．
【解答】
解：A、名)，则样本容量是200，故A正确；
B、成绩为A的人数是：200×60%=120(人)，
成绩为D的人数是200−120−50−20=10(人)，
所以D等所在扇形的圆心角为：360°×10200=18°，故B错误；
C、样本中C等所占百分比是1−60%−25%−10200×100%=10%，故C正确；
D、全校学生成绩为A等大约有1500×60%=900(人)，故D正确；
由于该题选择错误的，故选：B．
8.【答案】D
【解析】
【分析】
本题考查了扇形统计图，掌握百分比和圆心角的计算方法是解题的关键.根据百分比和圆心角的计算方法计算即可．
【解答】
解：A.认为依情况而定的占27%，故A正确；
B.认为该扶的在统计图中所对应的圆心角是65%×360°=234°，故B正确；
C.认为不该扶的占1−27%−65%=8%，故C正确；
D.认为该扶的占65%，故D错误．
故选：D．
9.【答案】A
【解析】解：(7+2+13+11+7)÷5=8，即平均数是8，故A是正确的．
出现次数最多的是7，即众数是7，故B不正确，
从小到大排列，第3个数都是7，即中位数是7，故C是不正确的；
极差为13−2=11，故D不正确；
故选：A．
从条形统计图中可以知道，选择公交7人，火车2人，地铁13人，轻轨11人，其它7人，
极差为13−2=11，故D不正确；出现次数最多的是7，即众数是7，故B不正确，从小到大排列，第3个数都是7，即中位数是7，故C是不正确的；
(7+2+13+11+7)÷5=8，即平均数是8，故A是正确的．
考查平均数、众数、中位数、极差的意义和求法，正确掌握这几个统计量的意义是解决问题的前提．
10.【答案】A
【解析】解：A、将这组数据按从小到大的顺序排列为19677，19791，21126，24268，25855，26547，29285，35581，39513，67366，
位于中间的两个数分别是25855，26547，所以中位数是25855+265472=26201(万美元)，
故本选项说法正确，符合题意；
B、根据折线图可知，对印度尼西亚的出口额比去年同期增长27.3%，故本选项说法错误，不符合题意；
C、去年同期对日本的出口额为：355811+31.4%≈27078.4，对俄罗斯联邦的出口额为：395131+66.0%≈23803.0，
故本选项说法错误，不符合题意；
D、根据折线图可知，出口额同比增速中，对越南的增速最快，故本选项说法错误，不符合题意；
故选：A．
根据中位数的定义，求出对10个国家出口额的中位数，即可判断A；
根据折线图可知，对印度尼西亚的出口额比去年同期增长27.3%，即可判断B；
分别求出去年同期对日本的出口额，对俄罗斯联邦的出口额，即可判断C；
根据折线图即可求解根据判断D．
考查了中位数．本题为统计题，中位数是将一组数据从小到大(或从大到小)重新排列后，最中间的那个数(最中间两个数的平均数)，叫做这组数据的中位数，如果中位数的概念掌握得不好，不把数据按要求重新排列，就会错误地将这组数据最中间的那个数当作中位数．
11.【答案】D
【解析】略
12.【答案】D
【解析】解：A.1995～1999年，国内生产总值的年增长率逐年减小，此选项正确；
B.2000年国内生产总值的年增长率开始回升，此选项正确；
C.这7年中，每年的国内生产总值不断增长，此选项正确；
D.这7年中，每年的国内生产总值的增长率有增有减，而国内生产总值不断增长，此选项错误；
故选：D．
根据题意，根据增长率的意义：这7年中，每年的国内生产总值增长率为正．故这7年中，每年的国内生产总值不断增长，据此即可作出判断．
本题考查的是折线统计图的综合运用．读懂统计图，从统计图中得到必要的信息是解决问题的关键．折线统计图表示的是事物的变化情况．
13.【答案】70
【解析】调查的总人数：(40+50+10)÷(1−15%−35%)=200，
“非常满意”的人数：200×15%=30，
因此“非常满意”和“满意”的总人数为30+40=70．
14.【答案】24
【解析】 选最喜爱“体操”的学生占总人数的1−40%−10%−35%=15%，
∵选最喜爱“体操”的学生有9人，
∴这次调查的总人数为9÷15%=60，
∴最喜爱“3D打印”的学生人数为60×40%=24．
15.【答案】162°
【解析】解：在扇形统计图中，代表体育优秀扇形的圆心角是360°×1840=162°，
故答案为：162°．
先求出体育优秀的占总体的百分比，再乘以360°即可．
本题考查扇形统计图及相关计算．在扇形统计图中，每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°比．
16.【答案】①②③④
【解析】
【分析】
本题考查了折线统计图：折线图是用一个单位表示一定的数量，根据数量的多少描出各点，然后把各点用线段依次连接起来．以折线的上升或下降来表示统计数量增减变化．折线图不但可以表示出数量的多少，而且能够清楚地表示出数量的增减变化情况．
利用折线统计图1可判断18日对应的PM2.5浓度的值最小，则可①进行判断；根据21日对应的PM2.5浓度最高，则可对②进行判断；利用折线统计图2找出AQI不大于100的数据可对③进行判断；结合两个折线统计图，比较每天的PM2.5浓度和空气质量指数AQI可对④进行判断．
【解答】
解：18日的PM2.5浓度最低，为25，所以①正确；
21日对应的PM2.5浓度最高所以②正确；
这六天中，18日、19日、20日、23日的空气质量为“优良”，所以③正确；
空气质量指数AQI与PM2.5浓度有关，PM2.5浓度越大，空气质量指数AQI越大，所以④正确．
故答案为①②③④．
17.【答案】60°
【解析】解：甲地区扇形圆心角∠AOB的度数为360°×22+7+3=60°，
故答案为：60°．
用360°乘以甲地区人数占总人数的比例即可．
本题考查了扇形统计图的知识，解答本题的关键是求出甲地区人数所占的比例，另外要求掌握扇形统计图的特点．
18.【答案】解：(1)选择两家酒店月盈利的平均值；
xA−=1+1.6+2.2+2.7+3.5+46=2.5，
xB−=2+3+1.7+1.8+1.7+3.66=2.3；
(2)平均数，方差反映酒店的经营业绩，A酒店的经营状况较好．
理由：A酒店盈利的平均数为2.5万元，B酒店盈利的平均数为2.3万元．A酒店盈利的方差为1.073平方万元，B酒店盈利的方差为0.54平方万元，无论是盈利的平均数还是盈利的方差，都是A酒店比较大，且盈利折线A是持续上升的，故A酒店的经营状况较好．
【解析】此题考查了折线统计图的知识．此题难度适中，注意掌握折线统计图表达的实际意义是解此题的关键．
(1)由要评价两家酒店月盈利的平均水平，即可得选择两家酒店月盈利的平均值，然后利用求平均数的方法求解即可求得答案；
(2)平均数，盈利的方差反映酒店的经营业绩，A酒店的经营状况较好．
19.【答案】解：(1)100；20；144；
(2)被抽取同学的平均体重为：
1100(40×10+45×20+50×40+55×20+60×10)=50(千克)．
答：被抽取同学的平均体重为50千克．
(3)1000×10+20100=1000×30%=300(人)．
答：七年级学生体重低于47.5千克的学生大约有300人．
【解析】本题考查的是频数分布表和扇形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．频数分布表能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
(1)由频数分布表和扇形统计图可知，m=100，n=20，圆心角为40100×360°=144°；
(2)各组体重值的中间值乘以各组人数，再求和，除以总人数即可得到答案；
(3)由题可知，有10+20=30名体重低于47.5千克的学生，然后根据1000×30%=300人，便可得出结果．
【解答】
解：(1)①m=20÷20%=100，
②n=100−10−40−20−10=20，
③c=40100×360°=144°；
故答案为100；20；144；
(2)见答案
(3)见答案．
20.【答案】解：(1)18；
(2)解：A组人数为240−204−12=24，
补全图如下：
；
(3)30000×85%=25500(人)．
答：估计该区30000名中学生家长中有25500人持赞成态度．
【解析】
【分析】
本题考查的是扇形统计图，条形统计图，样本容量，样本估计总体等有关知识．
(1)先计算出样本容量204÷85%，再运用C组频数除以总数即可得到相应频率，再乘以360即可；
(2)用总数减去B，C两组人数即可得到A组人数；
(3)用30000去乘以C组的频率即可．
【解答】
解：(1)204÷85%=240，
12240×360°=18°．
故答案为18．
(2)见答案；
(3)见答案．
21.【答案】7 7 7.5 3
【解析】解：(1)小张的中位数为7，
小王的平均数=110(2+4+6+8+7+7+8+9+9+10)=7，
小王的中位数=7+82=7.5，
小王命中9环及以上次数为3．
故答案为：7，7，7.5，3．
(2)从平均数看两人的成绩一样，
从中位数来看小王的成绩比较好．
综上所述，小王的成绩比较好．
(3)从平均数和命中9环以上的次数相结合来看，小王的成绩比较好．
(4)从折线图上两人射击命中环数的走势相结合来看，小王更有潜力．
(1)根据中位数，平均数的定义求解即可．
(2)从平均数和中位数相结合来分析可得结论．
(3)从平均数和命中9环以上的次数相结合来分析可得结论．
(4)从折线图上两人射击命中环数的走势分析可得结论．
本题考查折线统计图，中位数，平均数等知识，解题的关键是理解中位数，平均数的定义，属于中考常考题型．
22.【答案】4 3 “钉钉” “钉钉”的众数、中位数都比“QQ直播”的众数、中位数大
【解析】解：(1)如图，补全的条形统计图如下：


(2)a=4+42=4，b=3．
故答案为：4，3；
(3)学生对这两款软件评价较高的是“钉钉”，
理由是：“钉钉”的众数、中位数都比“QQ直播”的众数、中位数大
故答案为：“钉钉”，“钉钉”的众数、中位数都比“QQ直播”的众数、中位数大；
(4)根据题意，得
4.4×60%+3.35×40%=3.98(分)，
4×60%+3.35×40%=3.74(分)，
∵3.98>3.74，
∴学校会采用“钉钉”软件进行教学．
(1)根据统计表中的数据，即可补全条形图；
(2)根据中位数和众数的定义即可填空；
(3)根据表格数据可得“钉钉”的众数、中位数都比“QQ直播”的众数、中位数大，进而可以进行评价；
(4)根据题意即可通过计算分析学校会采用哪款软件进行教学．
本题考查的是条形统计图的综合运用．读懂统计图，从统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据．
23.【答案】(1)16， 12.5 ；
(2)职工：16−4−2−4=6(万人)，如图所示：
(3)估计24000人次中是职工的人次为24000×616=9000(人次)．
【解析】
解：(1)在统计的这段时间内，到图书馆阅读的人数为4÷25%=16(万人)，
其中商人占百分比为216×100%=12.5%；
故答案为：16；12.5；
(2)见答案
(3)见答案．
【分析】
(1)利用到图书馆阅读的人数=学生的人数÷学生的百分比求解，商人占百分比=商人数÷总人数求解即可，
(2)求出职工到图书馆阅读的人数，作图即可，
(3)利用总人数乘读者是职工的人数所占的百分比求解即可．
本题主要考查了条形统计图与扇形统计图，解题的关键是读懂统计图，从统计图中得到准确的信息．
24.【答案】解：(1)50；
(2)样本数据的平均数为：
4×6+10×7+15×8+11×9+10×1050=8.26；
根据条形统计图可知众数为8；
中位数为从大到小(或从小到大)排列的第25，第26的两个数据的平均值，
根据条形统计图可知中位数为8；
(3)1050×500=100
∴需要准备100份“一等奖”奖品．
【解析】
【分析】
本题考查条形统计图，平均数，众数，中位数，用样本估计总体，
(1)根据条形统计图，将各得分对应的人数相加即为所求；
(2)结合条形统计图的数据，结合平均数，众数，中位数的概念进行解答即可；
(3)用样本中得10分的比值，乘以500即可得到结果．
【解答】
解：(1)根据条形统计图可知，
本次调查一共抽取居民为：
4+10+15+11+10=50(名)
故答案为50；
(2)见答案；
(3)见答案．
25.【答案】(1)a=7，b=7.5，c=50%；
(2)八年级学生掌握垃极分类知识较好，理由：
七、八年级的平均数相同，但八年级的众数、中位数以及8分及以上人数所占百分比大于七年级，故八年级学生掌握垃极分类知识较好；
(3)∵从调查的数据看，七年级2人的成绩不合格，八年级2人的成绩不合格，
∴参加此次测试活动成绩合格的学生有1200×(20−2)+(20−2)20+20=1080(人)，
答：参加此次测试活动成绩合格的学生有1080人．
【解析】(1)∵七年级20名学生的测试成绩为：7，8，7，9，7，6，5，9，10，9，8，5，8，7，6，7，9，7，10，6，
∴众数a=7，
由条形统计图可得，中位数b=(7+8)÷2=7.5，
c=(5+2+3)÷20×100%=50%，
即a=7，b=7.5，c=50%；
(2)根据题意，即可得解；
(3)根据题目中的数据和条形统计图中的数据，进行求解即可．
本题考查条形统计图、中位数、众数、用样本估计总体．
选修课
A
B
C
D
E
F
人数
20
30
组别
体重(千克)
人数
A
37.5≤x<42.5
10
B
42.5≤x<47.5
n
C
47.5≤x<52.5
40
D
52.5≤x<57.5
20
E
57.5≤x<62.5
10
平均数
中位数
命中9环及以上次数
小张
7
______
1
小王
______
______
______
钉钉
5
4
5
1
4
2
5
3
4
1
1
3
5
4
2
4
4
3
2
5
QQ直播
4
3
3
3
5
5
3
4
5
2
2
5
4
4
4
1
3
2
3
2
软件
平均数
众数
中位数
钉钉
3.35
4
A
QQ直播
3.35
B
3
年级
平均数
众数
中位数
8分及以上人数所占百分比
七年级
7.5
a
7
45%
八年级
7.5
8
b
c