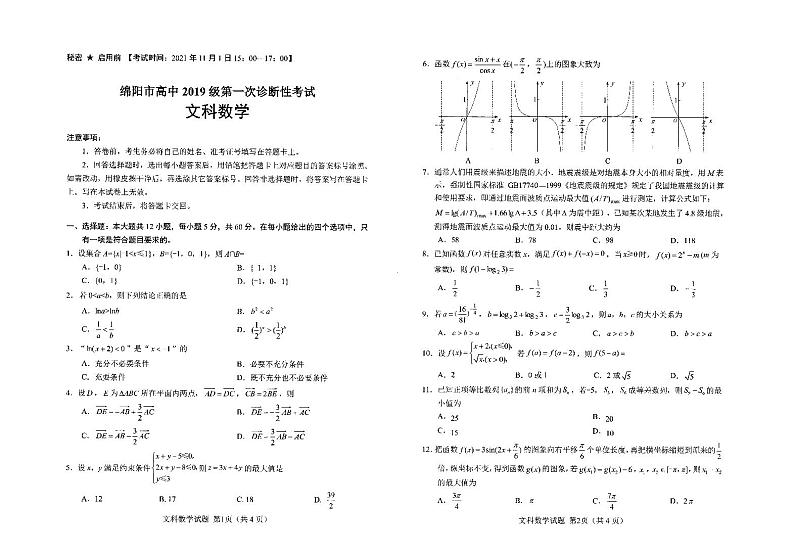
四川省绵阳市2022届高三上学期第一次诊断性考试（11月） 数学（文） PDF版含答案

这是一份四川省绵阳市2022届高三上学期第一次诊断性考试（11月） 数学（文） PDF版含答案，文件包含数学文科答案doc、数学文pdf等2份试卷配套教学资源，其中试卷共9页， 欢迎下载使用。
绵阳市高中2019级第一次诊断性考试文科数学参考答案及评分意见 一、选择题：本大题共12小题，每小题5分，共60分．       CDADC     ACBBA    BC二、填空题：本大题共4小题，每小题5分，共20分．13．7         14．2                     15．                  16．[1，] 三、解答题：本大题共6小题，共70分． 17．解：（1）由题意得A=2，，∴．…………………………………………………………………………2分∵函数的图象经过点，∴．又|φ|＜ ，∴． …………………………………………………………5分∴． …………………………………………………………6分由，得．∴函数的单调递增区间为[，]()． ……………8分（2）∵，∴，∴， ∴函数的值域为[-1，2]． ………………………………………………12分18．解：（1）当n=1时，=，解得．  …………………………………………………………………… 2分∵，①∴当时，．②①－②得， 整理得(n≥2) ．∴数列是以首项为2，公比为2的等比数列．   …………………………5分∴． ………………………………………………………………………6分（2）由（1）得．   ………………………………………………7分 ∴ ．   …………………………12分19．解：选择条件①： 由，得，由正弦定理可得，.∴，∴，∵，∴，∴，又，∴．选择条件②：由正弦定理可得，，又，∴，化简整理得，由，故，又，∴．选择条件③：由已知得，，由余弦定理，得，∵，∴，∵，∴，由正弦定理，有，∵，∴. 又，∴．  …………………………………………………………6分（2）∵，∴．  …………………………………………8分∵△ABC为锐角三角形，则， ∴．  …………………………………………………………………10分∴． ……………………………………………………………………12分20．解：（1）由题意得-(x-3a)(x+a)．…………………1分当时，，[-4，2]． 由，解得；由，解得或．    ……………………………………3分∴函数f(x)在区间(-3，1)上单调递增，在区间[-4，-3)，(1，2]单调递减．又 ，∴函数在区间[-4，2]上的最大值为0，最小值为．    ……………6分（2）函数f(x)只有一个零点．∵，i)当a<0时，由，解得，∴函数f(x)在区间(3a，-a)上单调递增；由，解得或，∴函数f(x)在区间(，3a)，(-a，)上单调递减．又，∴只需要f (-a)<0，解得-1<a<0．∴实数a的取值范围为 -1<a<0． ii)当a=0时，显然f(x)只有一个零点成立．   ………………………………10分   iii) 当a>0时，由，解得，即f(x)在区间(-a， 3a)上单调递增；由，解得或，即函数f(x)在区间(，-a)，(3a，)上单调递减；又，∴只需要f(3a)<0，解得．综上：实数a的取值范围是．  ………………………………………12分21．解：（1）由题意得． ………………………………2分∵函数f(x)的图象在点(0，f(0))处的切线的斜率为-3，∴，解得b=2． ………………………………………………………………………4分（2）∵ f(x)>-e-1恒成立，∴f(1)=-e+a-2>-e-1，即a>1．∴f(x)≥(x-2)ex+x2-2x(当x=0时，取“=”)．    ……………………………6分令g(x)=(x-2)ex+x2-2x，则．由，得x>1，由，得x<1．∴函数g(x)在区间(，1)上单调递减，在区间(1，)上单调递增．  ……………………………………8分∴-e-1，∴g(x)≥-e-1(当x=1时，取“=”) ．∴f(x)>-e-1．综上，实数a的取值范围为a>1．   …………………………………………12分22．解：（1）曲线的极坐标方程为．  …………………………2分      设P()为曲线上的任意一点，可得．  ∴曲线极坐标方程为． …………………………………5分（2）∵直线与曲线，分别相交于点A，B，∴设B()，则A()．由题意得，， ∴． ……………………………………………………7分∵点M到直线AB的距离，∴ ．∴△ABM的面积的最大值为．  ……………………………………………10分23．解：（1）由题意得． ………3分 ∵函数的最大值为6， ∴，即． ∵m>0，∴m=2.         ……………………………………………………………5分（2）由（1）知，，∵x>0，y>0，z>0，        ∴ (当且仅当时，等号成立)．  …………………………8分∴，      ∴(当且仅当时，等号成立)．   ………………10分