2020-2021学年江西省赣州市某校初一（下）5月月考数学试卷新人教版

这是一份2020-2021学年江西省赣州市某校初一（下）5月月考数学试卷新人教版，共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1. 下列四个实数中，最小的是( )
A.−2B.−5C.1D.4

2. 下列方程组中，是二元一次方程组的是( )
A.x+y=1，y=x2B.3x+y=1，2y−z=6
C.x+y=1，xy=1D.x=6，y−2x=4

3. 在下列给出坐标的点中，在第二象限的是( )
A.(2, 3)B.(−2, 3)C.(−2, −3)D.(2, −3)

4. 已知x=2,y=1是方程kx+y=3的一个解，那么k的值是( )
A.2B.−2C.1D.−1

5. 下列各项中，蕴含不等关系的是( )
A.老师的年龄是你的年龄的2倍B.小军和小红一样高
C.小明岁数比爸爸小26岁D.x2是非负数

6. 已知x=−1，y=2是二元一次方程组3x+2y=m，nx−y=1的解，则m−n的值是( )
A.1B.2C.3D.4
二、填空题

比较大小：4________15(填“>”、“<”或“=”).

如图，一条公路两次转弯后又回到原来的方向．若第一次转弯时∠B=140∘，则∠C的度数是________.


如图，把三角板的斜边紧靠直尺平移，一个顶点从刻度“5”平移到刻度“10”，则顶点C平移的距离CC′=_______.
.

已知甲队有x人，乙队有y人，若从甲队调出10人到乙队，则乙队人数是甲队人数的2倍，调整后两队人数间的数量关系用方程表示为________．

一次普法知识竞赛共有30道题，规定答对一题得4分，答错或者不答倒扣一份，在这次竞赛中小明获得优秀(90分或90分以上)，则小明至少答对了________道题.

若关于x，y的方程组x+y=3，x−2y=a−2的解是正整数，则整数a的值是________．

如图，梯形ABCD中，AD // BC，E在BC上，且∠A+∠1=180∘，则AB // DE．
理由如下：
∵ AD // BC(________)，
∴ ∠________+∠B=＝180∘(________)，
又∵ ∠A+∠1=180∘(________)，
∴ ________，
∴ AB // DE(________).
三、解答题

计算：
(1)16+3−27−1+916；

(2)−22+|2−1|−2−1

解不等式2−x4≥1−x3，并把它的解集在数轴上表示出来．


解下列方程组：
(1){3x+y=7，2x−y=3；

(2){13x+1=y，2(x+1)−y=6.

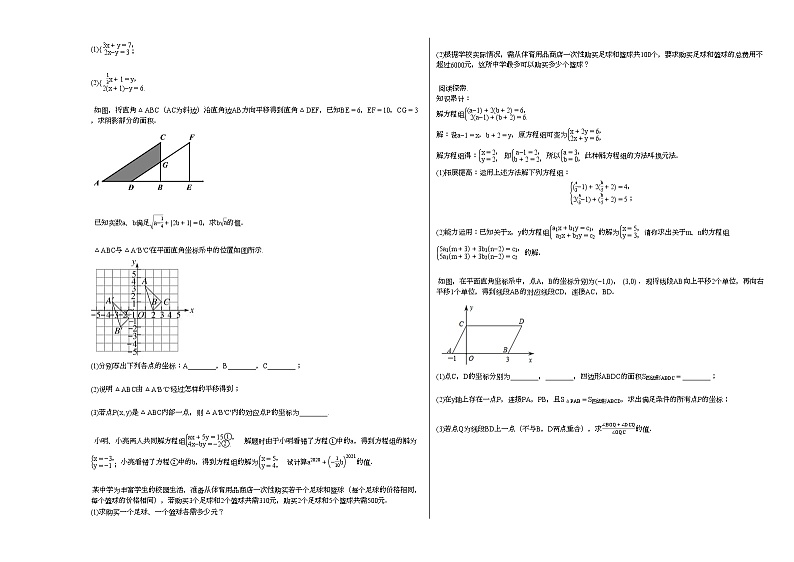
如图，将直角△ABC（AC为斜边）沿直角边AB方向平移得到直角△DEF，已知BE=6，EF=10，CG=3，求阴影部分的面积．


已知实数a、b满足a−14+|2b+1|=0，求ba的值．

△ABC与△A′B′C′在平面直角坐标系中的位置如图所示.

(1)分别写出下列各点的坐标：A________，B________，C________；

(2)说明△ABC由△A′B′C′经过怎样的平移得到；

(3)若点P(x, y)是△ABC内部一点，则△A′B′C′内的对应点P′的坐标为________.

小明、小亮两人共同解方程组ax+5y=15①，4x−by=−2②. 解题时由于小明看错了方程①中的a，得到方程组的解为x=−3，y=−1； 小亮看错了方程②中的b，得到方程组的解为x=5，y=4， 试计算a2020+−110b2021的值．

某中学为丰富学生的校园生活，准备从体育用品商店一次性购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格相同），若购买3个足球和2个篮球共需310元，购买2个足球和5个篮球共需500元．
(1)求购买一个足球、一个篮球各需多少元？

(2)根据学校实际情况，需从体育用品商店一次性购买足球和篮球共100个，要求购买足球和篮球的总费用不超过6000元，这所中学最多可以购买多少个篮球？

阅读探索.
知识累计：
解方程组(a−1)+2(b+2)=6，2(a−1)+(b+2)=6.
解：设a−1=x，b+2=y，原方程组可变为x+2y=6，2x+y=6，
解方程组得：x=2，y=2， 即a−1=2，b+2=2，所以a=3，b=0，此种解方程组的方法叫换元法．
(1)拓展提高：运用上述方法解下列方程组：
(a3−1)+2(b5+2)=4，2(a3−1)+(b5+2)=5；

(2)能力运用：已知关于x，y的方程组a1x+b1y=c1，a2x+b2y=c2的解为x=5，y=3，请你求出关于m、n的方程组5a1m+3+3b1n−2=c1，5a1m+3+3b2n−2=c2的解．

如图，在平面直角坐标系中，点A，B的坐标分别为−1,0， 3,0 ．现将线段AB向上平移2个单位，再向右平移1个单位，得到线段AB的对应线段CD，连接AC，BD．

(1)点C，D的坐标分别为________，________，四边形ABDC的面积S四边形ABDC=________；

(2)在y轴上存在一点P，连接PA，PB，且S△PAB=S四边形ABCD，求出满足条件的所有点P的坐标；

(3)若点Q为线段BD上一点（不与B，D两点重合），求∠BOQ+∠DCQ∠OQC的值．
参考答案与试题解析
2020-2021学年江西省赣州市某校初一（下）5月月考数学试卷
一、选择题
1.
【答案】
B
【考点】
实数大小比较
【解析】
此题暂无解析
【解答】
解：∵ |−5|>|−2|，
∴ −5<−2<1<4.
故选B.
2.
【答案】
D
【考点】
二元一次方程组的定义
【解析】
根据组成二元一次方程组的两个方程应共含有两个未知数，且未知数的项最高次数都应是一次的整式方程，判断各选项即可．
【解答】
解：A，第二个方程中未知数x是二次的，故A选项错误．
B，方程组中含有3个未知数，故B选项错误．
C，第二个方程是二次的，故C选项错误．
D，符合二元一次方程组的定义，故D选项正确．
故选D．
3.
【答案】
B
【考点】
点的坐标
【解析】
根据第二象限内点的坐标符号(−, +)进行判断即可．
【解答】
解：根据四个象限的符号特点：第一象限(+, +)；第二象限(−, +)；第三象限(−, −)；第四象限(+, −)，则可得在第二象限内的点是(−2, 3).
故选B．
4.
【答案】
C
【考点】
二元一次方程的解
【解析】
将方程的解代入方程得到关于k的一元一次方程，于是可求得k的值．
【解答】
解：将x=2,y=1代入方程kx+y=3，
得2k+1=3，解得k=1.
故选C．
5.
【答案】
D
【考点】
不等式的定义
【解析】
根据不等式的定义对四个选项进行逐一解答即可．
【解答】
解：A，B，C均是等量关系，故不符合题意；
D，由x2是非负数可知x2≥0，故符合题意．
故选D．
6.
【答案】
D
【考点】
二元一次方程组的解
【解析】
根据方程的解满足方程，可得关于m，n的方程，根据解方程，可得答案．
【解答】
解：由题意，得m=−3+4=1，−n−2=1，
解得n=−3，
m−n=1−(−3)=4．
故选D．
二、填空题
【答案】
>
【考点】
实数大小比较
【解析】
根据4=16即可比较大小．
【解答】
解：∵ 4=16，16>15，
∴ 4>15.
故答案为：>.
【答案】
140∘
【考点】
平行线的性质
【解析】
根据两直线平行，内错角相等可知是140∘
【解答】
解：∵ AB//CD，∠B=140∘，
∴ ∠C=∠B=140∘.
故答案为：140∘.
【答案】
5
【考点】
平移的性质
【解析】
根据平移的性质进行解答即可.
【解答】
解：∵ 把三角板的斜边紧靠直尺平移，一个顶点从刻度$"5"$平移到刻度$"10"$，
∴ 三角板向右平移了5个单位，
∴ 顶点C平移的距离CC′=5.
故答案为：5．
【答案】
y+10=2(x−10)
【考点】
由实际问题抽象出二元一次方程
【解析】
本题的等量关系有：甲队调出10人到乙队，则乙队人数是甲队人数的2倍，可以列出方程．
【解答】
解：由题意，知
y+10=2(x−10)．
故答案为：y+10=2(x−10)．
【答案】
24
【考点】
一元一次不等式的实际应用
【解析】
在这次竞赛中，小明获得优秀（90分或90分以上），即小明的得分≥90分，设小明答对了x题．就可以列出不等式，求出x的值．
【解答】
解：设小明答对了x题．
故 30−x×−1+4x≥90，
解得： x≥24，
即小明至少答对了24道题．
故答案为： 24.
【答案】
2或−1
【考点】
二元一次方程组的解
【解析】
利用加减消元法解二元一次方程组，得到x和y关于a的解，根据方程组的解是正整数，得到5−a与a+4都要能被3整除，即可得到
答案．
【解答】
解：x+y=3，①x−2y=a−2，②
①−②得：3y=5−a，
解得：y=5−a3，
把y=5−a3代入①得：
x+5−a3=3，
解得：x=a+43，
∵方程组的解为正整数，
∴5−a与a+4都要能被3整除，
∴ a=2或−1．
故答案为：2或−1．
【答案】
解：∵ AD // BC（ 已知），
∴ ∠A+∠B=180∘（ 两直线平行，同旁内角互补），
又∵ ∠A+∠1=180∘（已知 ），
∴ ∠1=∠B，
∴ AB // DE（ 同位角相等，两直线平行）.
故答案为：已知；A；两直线平行，同旁内角互补；已知；∠1=∠B；同位角相等，两直线平行.
【考点】
平行线的判定与性质
【解析】
由AD // BC，根据两直线平行，同旁内角互补，易证∠A+∠B＝180∘，又由∠A+∠1＝180∘，易证得∠1＝∠B，继而证得结论．
【解答】
解：∵ AD // BC（ 已知），
∴ ∠A+∠B=180∘（ 两直线平行，同旁内角互补），
又∵ ∠A+∠1=180∘（已知 ），
∴ ∠1=∠B，
∴ AB // DE（ 同位角相等，两直线平行）.
故答案为：已知；A；两直线平行，同旁内角互补；已知；∠1=∠B；同位角相等，两直线平行.
三、解答题
【答案】
解：(1)原式=4+−3−2516
=4−3−54
=−14.
(2)原式=2+2−1−2+1
=2．
【考点】
实数的运算
算术平方根
立方根的应用
绝对值
【解析】


【解答】
解：(1)原式=4+−3−2516
=4−3−54
=−14.
(2)原式=2+2−1−2+1
=2．
【答案】
解：去分母得3(2−x)≥4(1−x)，
去括号得6−3x≥4−4x，
移项得4x−3x≥4−6，
合并得x≥−2，
在数轴上表示为：
．
【考点】
解一元一次不等式
在数轴上表示不等式的解集
【解析】
先去分母和去括号得到6−3x≥4−4x，然后移项后合并得到x≥−2，再利用数轴表示解集．
【解答】
解：去分母得3(2−x)≥4(1−x)，
去括号得6−3x≥4−4x，
移项得4x−3x≥4−6，
合并得x≥−2，
在数轴上表示为：
．
【答案】
解：(1)$\{\begin{matrix} {3x + y = 7\begin{matrix} \end{matrix}，①} \\ {2x - y = 3\begin{matrix} \end{matrix}，②} \\ \end{matrix}$
①+②得5x=10，
解得，x=2，
将x=2代入①，可得y=1.
故该方程组的解为{x=2，y=1.
(2){13x+1=y，①2(x+1)−y=6，②
①代入②，可得2x+2−13x−1=6.
解得，x=3，
将x=3代入①，可得y=2，
故方程组的解为{x=3，y=2.
【考点】
加减消元法解二元一次方程组
代入消元法解二元一次方程组
【解析】
（1）①+②可以消去y，将二元一次方程组化为一元一次方程，解一元一次方程就可解出x，将x代入①中即可解出y．
（2）将①代入②中可以消去y，将二元一次方程组化为一元一次方程，解一元一次方程就可解出x，将x代入①中即可解出y．
【解答】
解：(1)$\{\begin{matrix} {3x + y = 7\begin{matrix} \end{matrix}，①} \\ {2x - y = 3\begin{matrix} \end{matrix}，②} \\ \end{matrix}$
①+②得5x=10，
解得，x=2，
将x=2代入①，可得y=1.
故该方程组的解为{x=2，y=1.
(2){13x+1=y，①2(x+1)−y=6，②
①代入②，可得2x+2−13x−1=6.
解得，x=3，
将x=3代入①，可得y=2，
故方程组的解为{x=3，y=2.
【答案】
解：依题意可得：阴影部分的面积=梯形BEFG的面积.
又BE=6，EF=10，CG=3，
BG=BC−CG=EF−CG=10−3=7，
∴ 梯形BEFG的面积=12(BG+EF)⋅BE
=12×7+10×6
=51，
即所求阴影部分的面积是51.
【考点】
平移的性质
梯形的面积
【解析】
根据平移的性质可得△DEF=△ABC,S△DEF=S△ABC，则阴影部分的面积=梯形BEFG的面积，再根据梯形的面积公式即可得到答
案．
【解答】
解：依题意可得：阴影部分的面积=梯形BEFG的面积.
又BE=6，EF=10，CG=3，
BG=BC−CG=EF−CG=10−3=7，
∴ 梯形BEFG的面积=12(BG+EF)⋅BE
=12×7+10×6
=51，
即所求阴影部分的面积是51.
【答案】
解：根据题意得：a−14=0，2b+1=0，
解得：a=14，b=−12，
则ba=(−12)×14=−14．
【考点】
非负数的性质：算术平方根
非负数的性质：绝对值
【解析】
根据非负数的性质列出方程求出a、b的值，代入所求代数式计算即可．
【解答】
解：根据题意得：a−14=0，2b+1=0，
解得：a=14，b=−12，
则ba=(−12)×14=−14．
【答案】
(1, 3),(2, 0),(3, 1)
(2)△A′B′C′先向又平移4个单位，再向上平移2个单位得到△ABC.
(x−4, y−2)
【考点】
点的坐标
坐标与图形变化-平移
【解析】
此题暂无解析
【解答】
解：(1)由图可得：A(1, 3)，B(2, 0)，C(3, 1).
故答案为：(1, 3)；(2, 0)；(3, 1).
(2)△A′B′C′先向又平移4个单位，再向上平移2个单位得到△ABC.
(3)A(1, 3)变换到点A′的坐标是(−3, 1)，
故可以看出：横坐标减4，纵坐标减2，
∴ 点P的对应点P′ 的坐标是(x−4, y−2) .
故答案为：(x−4, y−2).
【答案】
解：根据题意，将x=−3，y=−1代入②，将x=5，y=4代入①得：
−12+b=−2，5a+20=15， 解得：a=−1，b=10，
则原式=(−1)2020+(−110×10)2021=1−1=0.
【考点】
二元一次方程组的解
【解析】
此题暂无解析
【解答】
解：根据题意，将x=−3，y=−1代入②，将x=5，y=4代入①得：
−12+b=−2，5a+20=15， 解得：a=−1，b=10，
则原式=(−1)2020+(−110×10)2021=1−1=0.
【答案】
解：(1)设购买一个足球x元、购买一个篮球y元，根据题意得
3x+2y=310，2x+5y=500，
解得：x=50，y=80，
∴ 购买一个足球50元、购买一个篮球80元.
(2)设最多买篮球m个，则买足球(100−m)个，根据题意得：
80m+50(100−m)≤6000，
解得：m≤3313，
∵ m为整数，
∴ m最大取33，
∴ 最多可以买33个篮球．
【考点】
二元一次方程组的应用——优化方案问题
一元一次不等式的运用
【解析】
（1）设一个足球、一个篮球分别为x、y元，就有3x+2y=310和2x+5y=500，由这两个方程构成方程组求出其解即可；
（2）设最多买篮球m个，则买足球(100−m)个，根据购买足球和篮球的总费用不超过6000元建立不等式求出其解即可．
【解答】
解：(1)设购买一个足球x元、购买一个篮球y元，根据题意得
3x+2y=310，2x+5y=500，
解得：x=50，y=80，
∴ 购买一个足球50元、购买一个篮球80元.
(2)设最多买篮球m个，则买足球(100−m)个，根据题意得：
80m+50(100−m)≤6000，
解得：m≤3313，
∵ m为整数，
∴ m最大取33，
∴ 最多可以买33个篮球．
【答案】
解：(1)设a3−1=x，b5+2=y，
方程组变形得：x+2y=4，2x+y=5，
解得：x=2，y=1，即a3−1=2，b5+2=1，
解得：a=9，b=−5.
(2)设5(m+3)=x，3(n−2)=y，可得5(m+3)=5，3(n−2)=3，
解得：m=−2，n=3.
【考点】
加减消元法解二元一次方程组
二元一次方程组的解
【解析】
（2）拓展提高
设a3−1=x，b5+2=y，根据（1）中的结论确定出关于x与y方程组，求出解得到x与y的值，即可求出a与b的值；
（3）能力运用
设5(m+3)=x3(n−2)=y，根据已知方程组的解确定出m与n的值即可．
【解答】
解：(1)设a3−1=x，b5+2=y，
方程组变形得：x+2y=4，2x+y=5，
解得：x=2，y=1，即a3−1=2，b5+2=1，
解得：a=9，b=−5.
(2)设5(m+3)=x，3(n−2)=y，可得5(m+3)=5，3(n−2)=3，
解得：m=−2，n=3.
【答案】
0,2,4,2,8
(2)设点P0,a，
根据题意，得：12×|a|×4=4×2，
解得a=±4，
∴ P0,4或P0,−4.
(3)如图，作QE//AB，交CO​于E.
∵ 线段CD是线段AB平移得到，
∴ CD//AB，
又∵QE//AB，
∴ CD//QE，
∴ ∠CQE=∠DCQ，
∵ QE//AB，
∴ ∠OQE=∠BOQ，
∴ ∠CQO=∠CQE+∠OQE=∠DCQ+∠BOQ，
∴ ∠BOQ+∠DCQ∠OQC=1.
【考点】
坐标与图形变化-平移
平移的性质
平行四边形的面积
三角形的面积
平行线的性质
【解析】
（1）由平移的性质可得C0,2， D4,2 ，由平行四边形的性质可求面积；
（2）设出P的坐标，用S△PAB=S四边形ABCD建立方程，解方程即可；
（3）作出辅助线，平行线，用两直线平行，内错角相等，即可．
【解答】
解：(1)∵ 点A，B的坐标分别为−1,0， 3,0 ，将线段AB向上平移2个单位，再向右平移1个单位，
∴ C0,2，D4,2，
由题意可知：四边形ABCD为平行四边形，
∴ S四边形ABCD=OC×AB=2×4=8.
故答案为：0,2； 4,2；8.
(2)设点P0,a，
根据题意，得：12×|a|×4=4×2，
解得a=±4，
∴ P0,4或P0,−4.
(3)如图，作QE//AB，交CO​于E.
∵ 线段CD是线段AB平移得到，
∴ CD//AB，
又∵QE//AB，
∴ CD//QE，
∴ ∠CQE=∠DCQ，
∵ QE//AB，
∴ ∠OQE=∠BOQ，
∴ ∠CQO=∠CQE+∠OQE=∠DCQ+∠BOQ，
∴ ∠BOQ+∠DCQ∠OQC=1.