2022年中考数学三轮冲刺讲义：第9讲《依据特征构造-补全模型》(含答案)学案

第9讲、依据特征构造——补全模型（讲义）

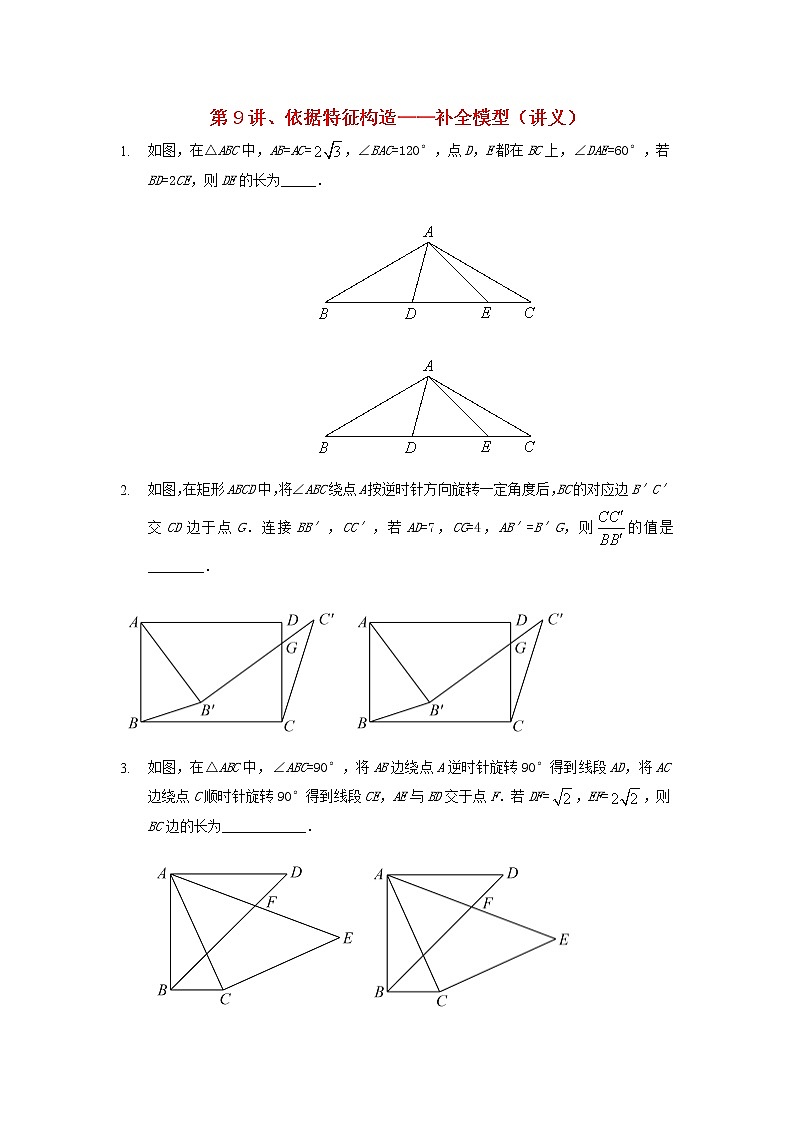
1. 如图，在△ABC中，AB=AC=，∠BAC=120°，点D，E都在BC上，∠DAE=60°，若BD=2CE，则DE的长为_____．

2. 如图，在矩形ABCD中，将∠ABC绕点A按逆时针方向旋转一定角度后，BC的对应边B′C′交CD边于点G．连接BB′，CC′，若AD=7，CG=4，AB′=B′G，则的值是________．

3. 如图，在△ABC中，∠ABC=90°，将AB边绕点A逆时针旋转90°得到线段AD，将AC边绕点C顺时针旋转90°得到线段CE，AE与BD交于点F．若DF=，EF=，则BC边的长为____________．

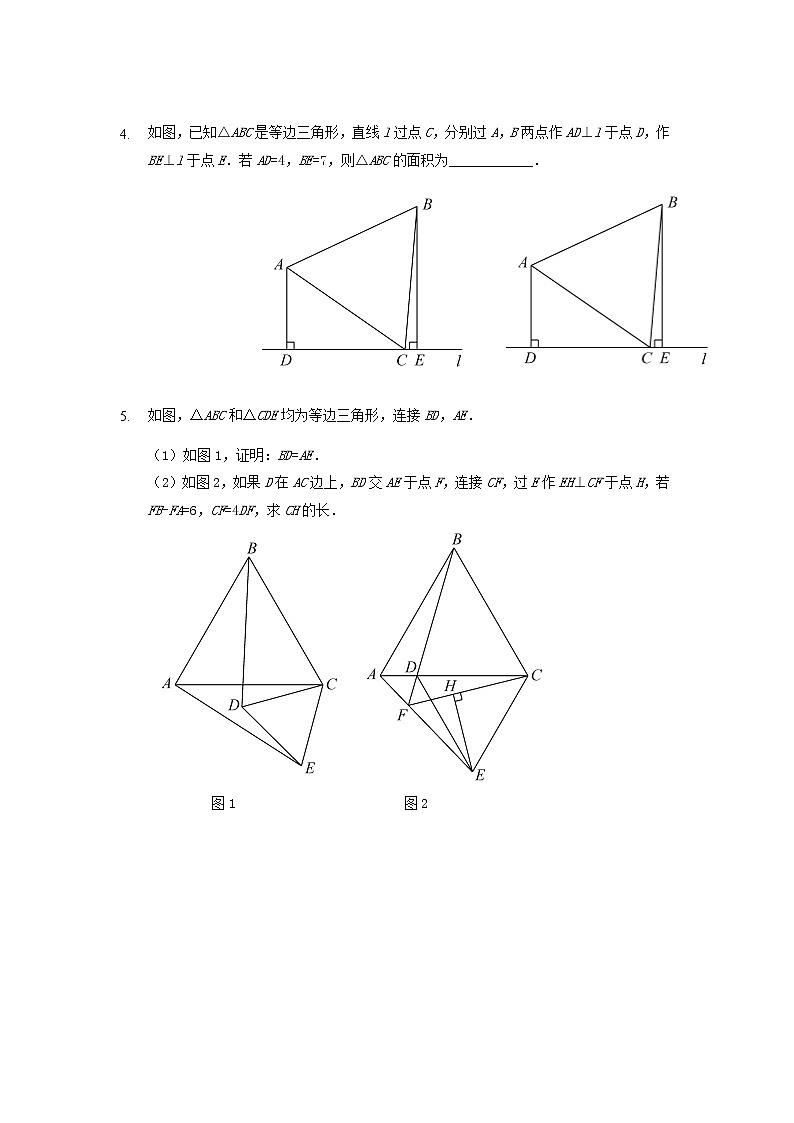
4. 如图，已知△ABC是等边三角形，直线l过点C，分别过A，B两点作AD⊥l于点D，作BE⊥l于点E．若AD=4，BE=7，则△ABC的面积为____________．

5. 如图，△ABC和△CDE均为等边三角形，连接BD，AE．

（1）如图1，证明：BD=AE．

（2）如图2，如果D在AC边上，BD交AE于点F，连接CF，过E作EH⊥CF于点H，若FB-FA=6，CF=4DF，求CH的长．

图1                        图2

6. 如图，在平面直角坐标系中，点O为坐标原点，抛物线y=x2+bx+c交x轴于A，B两点，交y轴于点C，直线y=x-3经过B，C两点．

（1）过点C作直线CD⊥y轴交抛物线于另一点D，点P是直线CD下方抛物线上的一个动点，且在抛物线对称轴的右侧，过点P作PE⊥x轴于点E，PE交CD于点F，交BC于点M，连接AC，过点M作MN⊥AC于点N，设点P的横坐标为t，线段MN的长为d，求d与t之间的函数关系式（不要求写出自变量t的取值范围）；

（2）在（1）的条件下，连接PC，过点B作BQ⊥PC于点Q（点Q在线段PC上），BQ交CD于点T，连接OQ交CD于点S，当ST=TD时，求线段MN的长．

7. 如图，在平面直角坐标系中，直线与x轴交于点A，与y轴交于点C，抛物线经过A，C两点，与x轴的另一交点为点B．

（1）求抛物线的函数表达式．

（2）点D为直线AC上方抛物线上一动点．

①连接BC，CD，设直线BD交线段AC于点E，△CDE的面积为S1，△BCE的面积为S2，求的最大值．

②过点D作DF⊥AC，垂足为点F，连接CD，是否存在点D，使得△CDF中的某个角恰好等于∠BAC的2倍？若存在，求点D的坐标；若不存在，请说明理由．

【参考答案】

5. （1）证明略；

（2）CH的长为．

6. （1）；

（2）线段MN的长为．

7. （1）抛物线的函数表达式为；

（2）①的最大值为；

②存在，点D的坐标为(-2，3)，(，)．