

初中第四章 图形的相似综合与测试练习题
展开第四章《图形的相似》检测卷(一)
一、 选择题(本大题共10小题,每小题3分,共30分)
1.两地的实际距离是1000 m.在地图上量得这两地的距离是1cm.则这幅地图的比例尺为( )
A.1∶1000 B.1∶10000 C.1∶100000 D.1∶1000000
2.如图,中,,,若,,则( )
A. B. C.4 D.
3.如图,在中,,,分别是边,,上的点,,,且,那么的值为( )
A. B. C. D.
4.如图,原点在网格格点上的平面直角坐标系中,两个三角形(顶点均在网格的格点上)是以点为位似中心的位似图形,则点的坐标是( )
A. B. C. D.
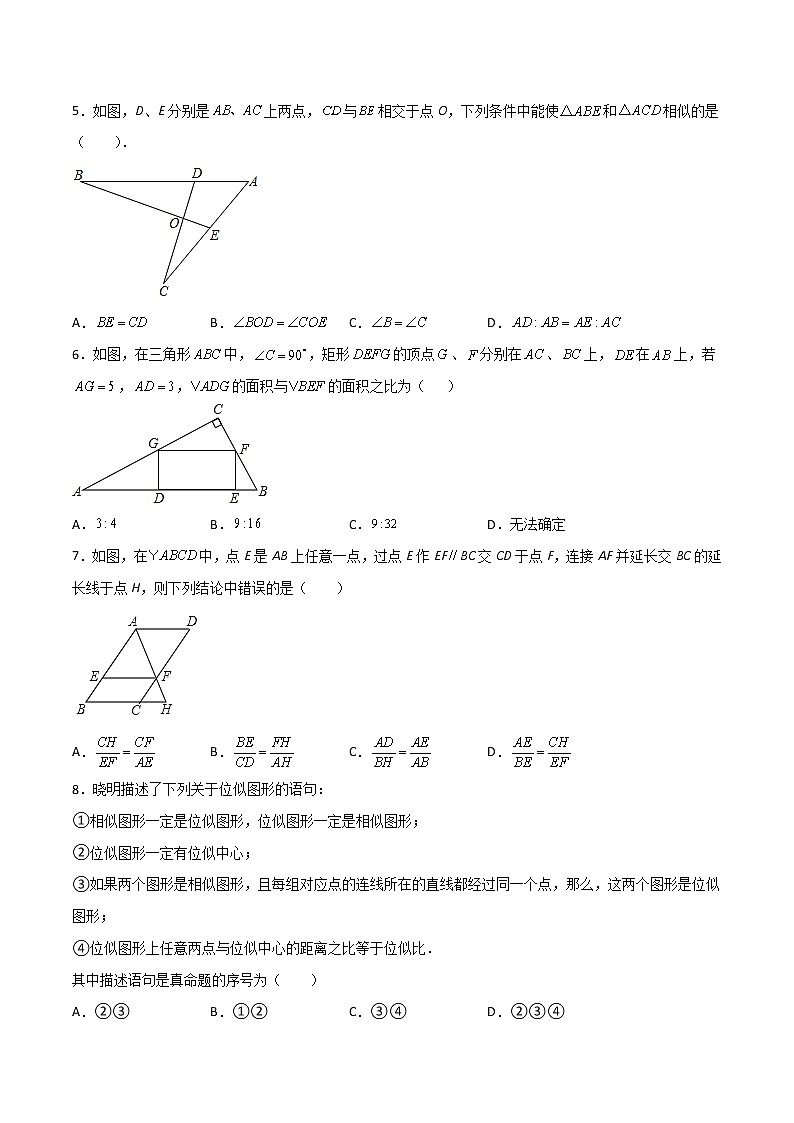
5.如图,D、E分别是上两点,与相交于点O,下列条件中能使和相似的是( ).
A. B. C. D.
6.如图,在三角形中,,矩形的顶点、分别在、上,在上,若,,的面积与的面积之比为( )
A. B. C. D.无法确定
7.如图,在中,点E是AB上任意一点,过点E作EFBC交CD于点F,连接AF并延长交BC的延长线于点H,则下列结论中错误的是( )
A. B. C. D.
8.晓明描述了下列关于位似图形的语句:
①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;
④位似图形上任意两点与位似中心的距离之比等于位似比.
其中描述语句是真命题的序号为( )
A.②③ B.①② C.③④ D.②③④
9.已知,则=( )
A. B. C. D.
10.如图,在中,,分别是边上的中线与高,,的面积为,则的长为( )
A. B. C. D.
二、填空题(本大题共7小题,每小题4分,共28分)
11.已知,且,则______.
12.如图,在中,点D,E分别是的中点,与相交于点F,若,则的长是______.
13.若,则=_____.
14.如图,在平行四边形ABCD中,点E是DC中点,BE与AC相交于点O,如果△EOC的面积是1,那么△ABC的面积是______.
15.下图是一架梯子的示意图,其中,且.为使其更稳固,在,间加绑一条安全绳(线段),量得,则________.
16.如图,是以点为位似中心经过位似变换得到的三角形,若的面积与的面积比是,则等于_______.
17.(1)若,则,请说明理由.
(2)已如线段.C为AB的黄金分割点,则线段___________cm.说明理由
三、解答题(一)(本大题共3小题,每小题6分,共18分)
18.如图,在中,的面积为25,点分别在边上,,已知.
(1)求的长.
(2)求四边形的面积.
19.小明想用刚学过的知识测量一棵大树的高度,他和学习小组的同学带着测量工具来到这棵大树前,将镜子放在离大树32m的C处(即),然后沿直线后退,在点D处恰好看到旗杆顶端B在镜子中的像与镜子上的标记重合.根据物理知识可知:反射角等于入射角,即.若小明的眼睛离地面高度为1.5m,,求大树的高度.(小平面镜的大小忽略不计)
20.如图,在由边长为1的小正方形组成的网格图中,已知点O及的顶点均为网格线的交点.
(1)将绕着点B顺时针旋转90°,得到,请在网格中画出;
(2)以点O为位似中心,将放大为原来的三倍,得到,请在网格中画出.
四、解答题(二)(本大题共3小题,每小题8分,共24分)
21.如图,四边形ABCD是平行四边形,E为边CD延长线上一点,连接BE交边AD于点F.
(1)找出图中所有的相似三角形(不再添加辅助线),它们分别是_____.
(2)请在你找出的各对相似三角形中,选择一对加以证明.
22.如图,在平面直角坐标系中, 三个顶点的坐标分别为,点坐标为.
(1)画出将向左平移5个单位长度的;
(2)画出和以点为位似中心的位似图形,和位似比为2:1,且位于点的两侧.
(3)直接写出三个点的坐标.
23.若与相交于点.,,,,证明.
五、解答题(三)(本大题共2小题,每小题10分,共20分)
24.已知,求的值.
25. 在的方格纸中,点都在格点上,按要求画图:
在图1中找-一个格点,使以点为顶点的四边形是平行四边形.
在图2中仅用无刻度的直尺,把线段分成两部分,使得这两部分长度之比为(保留画图痕迹,不写画法).
参考答案
二、 选择题(本大题共10小题,每小题3分,共30分)
1.两地的实际距离是1000 m.在地图上量得这两地的距离是1cm.则这幅地图的比例尺为( )
A.1∶1000 B.1∶10000 C.1∶100000 D.1∶1000000
【答案】C
【分析】
先把1000m化为100000cm,然后根据比例尺的定义求解.
【详解】
解:1000m=100000cm,
所以这幅地图的比例尺为1:100000.
故选:C.
【点睛】
本题考查了比例线段:对于四条线段a、b、c、d,如果其中两条线段的比(即它们的长度比)与另两条线段的比相等,如 a:b=c:d(即ad=bc),我们就说这四条线段是成比例线段,简称比例线段.
2.如图,中,,,若,,则( )
A. B. C.4 D.
【答案】C
【分析】
易证,根据相似三角形的性质列式计算,得到答案.
【详解】
解:∵,
∵,
∴,
∴,
∴,
∵AB=AD+BD=2+6=8,
∴,
解得,,
故选:C.
【点睛】
本题考查相似三角形的判定与性质,掌握相似三角形的判定方法与性质的应用是解题关键.
3.如图,在中,,,分别是边,,上的点,,,且,那么的值为( )
A. B. C. D.
【答案】A
【分析】
根据平行线分线段成比例定理,列出比例式求解即可得到答案.
【详解】
解:,,
,
又∵,
,
故选:.
【点睛】
此题考查了平行线分线段成比例定理的运用,熟练利用平行线分线段成比例定理是解题关键.
4.如图,原点在网格格点上的平面直角坐标系中,两个三角形(顶点均在网格的格点上)是以点为位似中心的位似图形,则点的坐标是( )
A. B. C. D.
【答案】A
【分析】
根据位似中心的概念作图,根据坐标与图形性质解答即可.
【详解】
解:分别连接、并延长交于点,
则点为位似中心,
故选:A.
【点睛】
本题考查的是位似图形的概念,掌握位似图形的对应顶点的连线相交于一点,这个点叫做位似中心是解题的关键.
5.如图,D、E分别是上两点,与相交于点O,下列条件中能使和相似的是( ).
A. B. C. D.
【答案】C
【分析】
根据已知及相似三角形的判定方法进行分析,从而得到答案.
【详解】
解: 根据相似三角形判定定理1:由 可知条件“∠B=∠C”可以推出两个三角形相似,故C符合题意;
根据相似三角形判定定理2:由 可知条件“AD∶AC=AE∶AB”,故D不符合题意.
而由条件“BE=CD”和“∠BOD=∠COE”无法推出和相似,故A、B不符合题意.
故选C.
【点睛】
本题考查了相似三角形的判定,①有两个对应角相等的三角形相似; ②有两个对应边的比相等,且其夹角相等,则两个三角形相似; ③三组对应边的比相等,则两个三角形相似.掌握以上知识是解题的关键.
6.如图,在三角形中,,矩形的顶点、分别在、上,在上,若,,的面积与的面积之比为( )
A. B. C. D.无法确定
【答案】B
【分析】
通过直角三角形的性质和矩形的性质得到,又根据,证明∽,得到,再根据勾股定理求出,进而得到,可知相似比为,最后根据相似三角形的性质得到面积比.
【详解】
,
,
四边形是矩形,
,,
,
,
∽,
,
在中,由勾股定理得:,
,,
,
,
,
的面积与的面积之比为.
故选:B.
【点睛】
本题主要考查了相似三角形的判定和性质,勾股定理,矩形的性质等知识,本题中求证∽是解题的关键.
7.如图,在中,点E是AB上任意一点,过点E作EFBC交CD于点F,连接AF并延长交BC的延长线于点H,则下列结论中错误的是( )
A. B. C. D.
【答案】D
【分析】
根据平行四边形的性质与相似三角形的判定与性质即可依次判断.
【详解】
解:∵四边形ABCD为平行四边形,EFBC,
∴AD=EF=BC,AE=DF,BE=CF.
A、∵ADCH,
∴△ADF∽△HCF,
∴,即,结论A正确;
B、∵ABCD,
∴△ABH∽△FCH,
∴,即,结论B正确;
C、∵ADBH,
∴△ADF∽△HBA,
∴,即,结论C正确;
D、∵AECF,EFCH,
∴△FCH∽△AEF,
∴,即,结论D错误.
故选:D.
【点睛】
本题考查了相似三角形的判定与性以及平行四边形的性质,根据相似三角形的性质逐一分析四个结论的正误是解题的关键.
8.晓明描述了下列关于位似图形的语句:
①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;
④位似图形上任意两点与位似中心的距离之比等于位似比.
其中描述语句是真命题的序号为( )
A.②③ B.①② C.③④ D.②③④
【答案】A
【分析】
分别利用位似图形的性质以及位似图形的定义分析得出答案.
【详解】
解:①相似图形不一定是位似图形,位似图形一定是相似图形,故错误;
②位似图形一定有位似中心,正确;
③如果两个图形是相似图形,且对应点的连线相交于一点,那么,这两个图形是位似图形,正确;
④位似图形上对应两点与位似中心的距离之比等于位似比,故错误.
故选A.
【点睛】
此题主要考查了位似图形的性质以及位似图形的定义,正确利用位似图形的性质分析是解题关键.
9.已知,则=( )
A. B. C. D.
【答案】D
【分析】
由题意易得,进而问题可求解.
【详解】
解:由可得:,
∴;
故选D.
【点睛】
本题主要考查比例的基本性质,熟练掌握比例的基本性质是解题的关键.
10.如图,在中,,分别是边上的中线与高,,的面积为,则的长为( )
A. B. C. D.
【答案】B
【分析】
先根据三角形面积和高AE的长求出底边BC的长,再根据AD是中线得到CD=BC,求出CD的长.
【详解】
解:∵S△ABC= =24, AE=8,
∴BC=6,
∵AD是BC上的中线,
∴CD=BC=3.
故选:B.
【点睛】
此题考查三角形的面积以及三角形中线以及高线的性质,根据已知得出BC的长是解题关键.
第II卷(非选择题)
二、填空题(本大题共7小题,每小题4分,共28分)
11.已知,且,则______.
【答案】2
【分析】
将化简为,再用a表示b代入,解之即可得.
【详解】
解:由化简为,,
将其代入为,
解得,
故答案为2.
【点睛】
本题考查了比例的性质,用代入消元法求解二元一次方程组;正确将已知变形是解题的关键.
12.如图,在中,点D,E分别是的中点,与相交于点F,若,则的长是______.
【答案】9
【分析】
根据中位线定理得到DE=AB,DE∥AB,从而证明△DEF∽△ABF,得到,求出EF,可得BE.
【详解】
解:∵点D,E分别为BC和AC中点,
∴DE=AB,DE∥AB,
∴△DEF∽△ABF,
∴,
∵BF=6,
∴EF=3,
∴BE=6+3=9,
故答案为:9.
【点睛】
本题考查了三角形中位线定理,相似三角形的判定和性质,解题的关键是根据中位线的性质证明△DEF∽△ABF.
13.若,则=_____.
【答案】
【分析】
根据,得到,代入式子计算即可.
【详解】
∵,
∴,
∴,
故答案为:.
【点睛】
此题考查代数式的求值,掌握等式的性质变形得到是解题的关键.
14.如图,在平行四边形ABCD中,点E是DC中点,BE与AC相交于点O,如果△EOC的面积是1,那么△ABC的面积是______.
【答案】6
【分析】
△ABO∽△CEO,且相似比为2:1,进而求得△ABO的面积为4,△OBC与△OEC分别选择OB、OE为底时,其高相同,得到△OBC与△OEC面积之比为2:1,由此求解.
【详解】
解:∵ABCD为平行四边形,
∴∠BAO=∠ECO,∠ABO=∠CEO,
∴△ABO∽△CEO,且相似比为AB:CE=2:1,
∵△EOC的面积等于1,
∴由相似三角形面积比等于相似比的平方可知,△ABO的面积为4,
又△OBC与△OEC分别选择OB、OE为底时,其高相同,
∴△OBC与△OEC面积之比等于底边OB:OE=2:1,
∴△BOC面积为2,
∴△ABC面积=△ABO面积+△BOC面积=4+2=6,
故答案为:6.
【点睛】
本题考查了相似三角形的判定和性质,熟练掌握相似三角形的面积之比等于相似比的平方这条性质是解决本题的关键.
15.下图是一架梯子的示意图,其中,且.为使其更稳固,在,间加绑一条安全绳(线段),量得,则________.
【答案】1.2
【分析】
根据平行线分线段成比例定理,可得,进而即可求解.
【详解】
解:∵,,
∴,
∵,
∴3,
故答案是:1.2.
【点睛】
本题主要考查平行线分线段成比例定理,掌握“平行线所截得的对应线段成比例”,是解题的关键.
16.如图,是以点为位似中心经过位似变换得到的三角形,若的面积与的面积比是,则等于_______.
【答案】2:3
【分析】
根据位似变换的概念得到△A'B'C'∽△ABC,B′C′∥BC,根据相似三角形的面积比等于相似比的平方计算即可.
【详解】
解:∵△A'B'C'是△ABC以点O为位似中心经过位似变换得到的三角形,
∴△A'B'C'∽△ABC,B′C′∥BC,
∵△A'B'C'的面积与△ABC的面积比是4:9,
∴,
∵B′C′∥BC,
∴△OB′C′∽△OBC,
∴OB':OB=B′C′:BC=2:3,
故答案为:2:3.
【点睛】
本题考查的是位似变换的概念和性质,如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形.
17.(1)若,则,请说明理由.
(2)已如线段.C为AB的黄金分割点,则线段___________cm.说明理由
【答案】(1)见解析;(2)或
【分析】
(1)先根据倒数的定义得出倒数相等,再等式两边都减去1,求出后根据等式的性质得出即可.
(2)根据黄金分割点的定义,知AC可能是较长线段,也可能是较短线段;根据黄金分割的定义即可得出答案.
【详解】
解:(1)∵,
∴,
∴,
∴,
∴,
∴;
(2)∵C为线段AB的黄金分割点,
则AC=8×=(cm),
或AC=8-()=(cm).
【点睛】
本题考查了比例的性质的应用,以及黄金分割的定义,线段上一点把线段分成两段,其中较长线段是较短线段和整个线段的比例中项,即较长线段是整个线段的倍,那么这个点就是这条线段的黄金分割点.
三、解答题(一)(本大题共3小题,每小题6分,共18分)
18.如图,在中,的面积为25,点分别在边上,,已知.
(1)求的长.
(2)求四边形的面积.
【答案】(1)(2)12
【分析】
(1)根据DE∥BC,可以证明△ADE∽△ABC,可得,可求出DE=CF,则BF可求出.
(2)根据相似三角形的面积的比等于相似比的平方,即可求得△ADE的面积,同理求得△BDF的面积,用△ABC的面积减去△ADE的面积和△BDF的面积即可求得.
【详解】
(1)∵,
∴,
∵DE∥BC,
∴△ADE∽△ABC,
∴,
∴,
∴DE=,
∵DE∥BC,DF∥AC,
∴四边形DECF为平行四边形,
∴DE=CF=,
∴BF=BC−CF=6−=;
(2)∵△ADE∽△ABC,
∴,
∴S△ADE=S△ABC=×25=4,
同理,S△BDF=S△ABC=×25=9.
∴平行四边形DFCE的面积为:25−S△ADE−S△BDF=25−4−9=12.
【点睛】
本题考查了相似三角形的判定与性质及平行四边形的判定与性质,正确理解相似三角形的性质,求得△ADE的面积和△BDF的面积是关键.
19.小明想用刚学过的知识测量一棵大树的高度,他和学习小组的同学带着测量工具来到这棵大树前,将镜子放在离大树32m的C处(即),然后沿直线后退,在点D处恰好看到旗杆顶端B在镜子中的像与镜子上的标记重合.根据物理知识可知:反射角等于入射角,即.若小明的眼睛离地面高度为1.5m,,求大树的高度.(小平面镜的大小忽略不计)
【答案】16米.
【分析】
根据等角的余角相等,解得,进而可证明,再由相似三角形对应边成比例的性质解题即可.
【详解】
,,
,
又,
,,,
解得:,
故大树的高度为16米.
【点睛】
本题考查相似三角形的应用,其中涉及等角的余角相等、相似三角形的判定与性质等知识,是重要考点,难度较易,掌握相关知识是解题关键.
20.如图,在由边长为1的小正方形组成的网格图中,已知点O及的顶点均为网格线的交点.
(1)将绕着点B顺时针旋转90°,得到,请在网格中画出;
(2)以点O为位似中心,将放大为原来的三倍,得到,请在网格中画出.
【答案】(1)如图见解析;(2)如图见解析.
【分析】
(1)直接利用旋转变换的性质得出对应点位置进而得出答案;
(2)直接利用位似图形的性质进而得出对应点位置进而得出答案.
【详解】
(1)如图所示,即为所求,
(2)如图所示,即为所求
【点睛】
此题主要考查了位似变换以及旋转变换,正确得出对应点位置是解题关键.
四、解答题(二)(本大题共3小题,每小题8分,共24分)
21.如图,四边形ABCD是平行四边形,E为边CD延长线上一点,连接BE交边AD于点F.
(1)找出图中所有的相似三角形(不再添加辅助线),它们分别是_____.
(2)请在你找出的各对相似三角形中,选择一对加以证明.
【答案】(1)△EAF∽△EBC,△CDF∽△EBC,△CDF∽△EAF,(2)选△EAF∽△EBC,理由见解析.
【分析】
(1)根据四边形ABCD是平行四边形可以得到对边平行,那么就存在“A”字型和“8”字型的相似三角形;
(2)结合平行线的性质,利用两组对应角相等证明三角形相似.
【详解】
(1)∵四边形ABCD是平行四边形,
∴,
∴△EAF∽△EBC,
∵,
∴△CDF∽△EAF,
∴△CDF∽△EBC,
故答案是:△EAF∽△EBC,△CDF∽△EBC,△CDF∽△EAF;
(2)选△EAF∽△EBC,
理由如下:在ABCD中AD∥BC,
∴∠EAF=∠B.
又∵∠E=∠E,
∴△EAF∽△EBC.
【点睛】
本题考查相似三角形的判定,解题的关键是掌握相似三角形的判定方法.
22.如图,在平面直角坐标系中, 三个顶点的坐标分别为,点坐标为.
(1)画出将向左平移5个单位长度的;
(2)画出和以点为位似中心的位似图形,和位似比为2:1,且位于点的两侧.
(3)直接写出三个点的坐标.
【答案】(1)画图见解析;(2)画图见解析;(3)
【分析】
(1)将A、B、C三个点都向左平移5个单位长度,得到、、,就可以画出;
(2)连接AE并延长至点,使,用同样的方法得到、,就可以画出;
(3)根据点的位置写出坐标.
【详解】
(1)如图所示:
(2)如图所示:
(3)由图可知:.
【点睛】
本题考查位似图形,解题的关键是掌握位似图形的画法.
23.若与相交于点.,,,,证明.
【答案】见解析
【分析】
根据条件证明,从而得到,最终得到.
【详解】
证明:∵,,
∴,
又∵,
∴,
∴,
∴.
【点睛】
本题考查相似三角形的判定与性质,熟练掌握相似三角形的判定方法是解题关键.
五、解答题(三)(本大题共2小题,每小题10分,共20分)
24.已知,求的值.
【答案】.
【分析】
可以设,则,,,把这三个式子代入所要求的式子,进行化简,即可求出式子的值.
【详解】
设,
则,,,代入可得,
.
【点睛】
利用这个题目中的设法,把三个未知数的问题转化为一个未知数的问题,是解题的关键.
25.在的方格纸中,点都在格点上,按要求画图:
在图1中找-一个格点,使以点为顶点的四边形是平行四边形.
在图2中仅用无刻度的直尺,把线段分成两部分,使得这两部分长度之比为(保留画图痕迹,不写画法).
【答案】(1)画图见解析;(2)画图见解析;
【分析】
(1)利用平行四边形的判定解决问题即可.
(2)利用平行线分线段成比例定理解决问题.
【详解】
解:(1)平行四边形ABCD如图1所示:
(2)如图2所示,取格点E,F连EF,线段EF把线段AB分成1:2;
或取格点G,H连GH,线段GH把线段AB分成1:2.
【点睛】
本题考查作图-应用与设计,平行四边形的判定,平行线分线段成比例定理等知识.
数学九年级上册第四章 图形的相似综合与测试同步训练题: 这是一份数学九年级上册第四章 图形的相似综合与测试同步训练题,共17页。试卷主要包含了若 ab=29 ,则a+bb,小刚身高 1等内容,欢迎下载使用。
初中数学北师大版九年级上册第三章 概率的进一步认识综合与测试练习题: 这是一份初中数学北师大版九年级上册第三章 概率的进一步认识综合与测试练习题,共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021学年第三章 概率的进一步认识综合与测试课后测评: 这是一份2021学年第三章 概率的进一步认识综合与测试课后测评,共27页。













