沪科版八年级上册13.1 三角形中的边角关系教学课件ppt

这是一份沪科版八年级上册13.1 三角形中的边角关系教学课件ppt，文件包含沪科版数学八年级上册131三角形中的边角关系-第2课时三角形中角的关系教学课件ppt、沪科版数学八年级上册131三角形中的边角关系-第2课时三角形中角的关系教案doc等2份课件配套教学资源，其中PPT共20页， 欢迎下载使用。

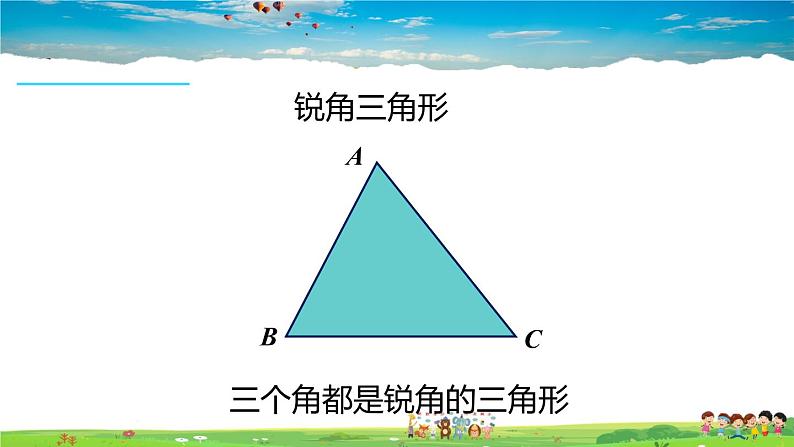
三个角都是锐角的三角形
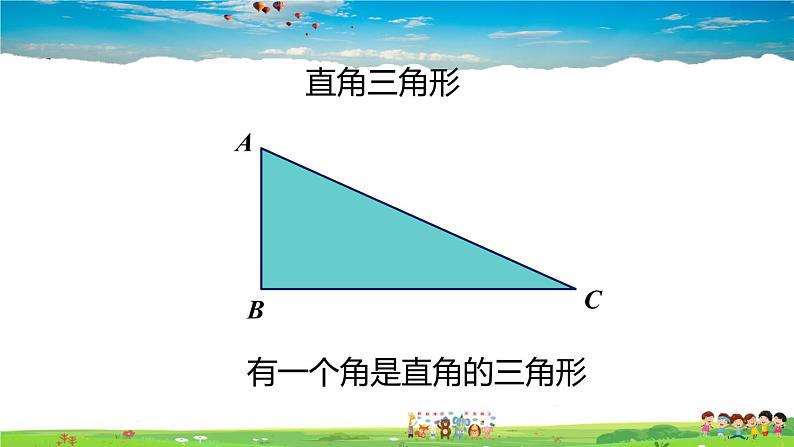
有一个角是直角的三角形
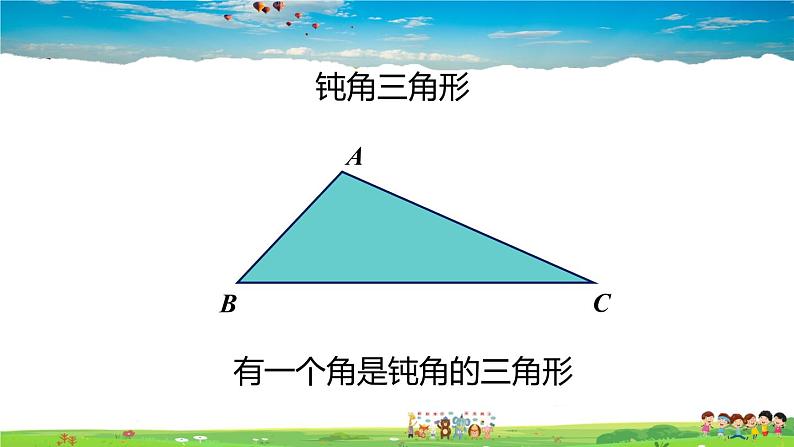
有一个角是钝角的三角形
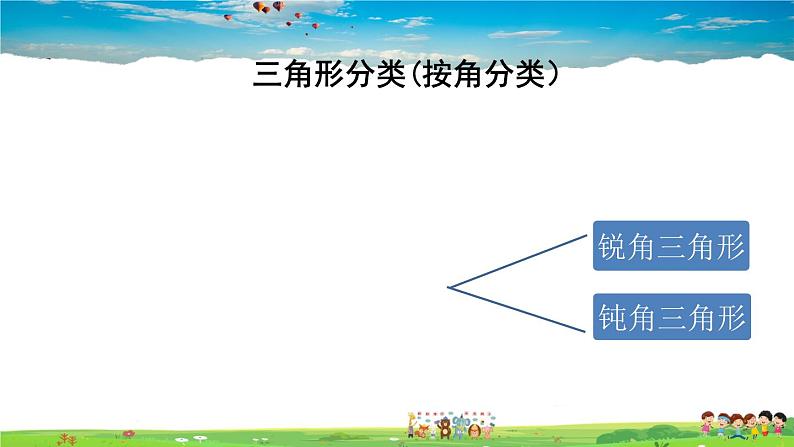
三角形分类(按角分类）
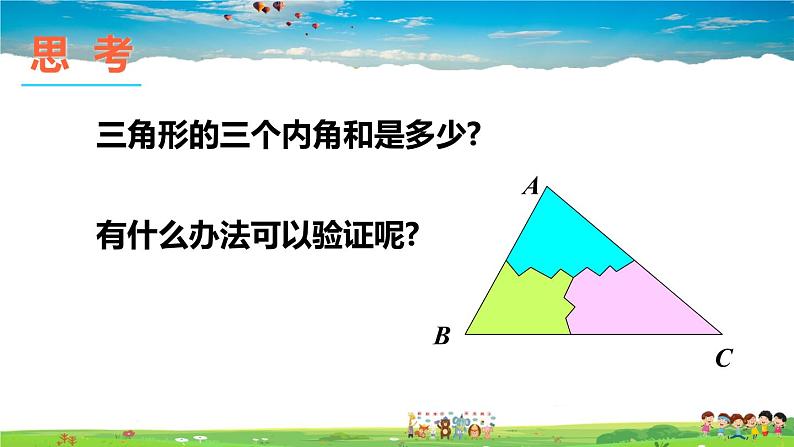
三角形的三个内角和是多少?
有什么办法可以验证呢?
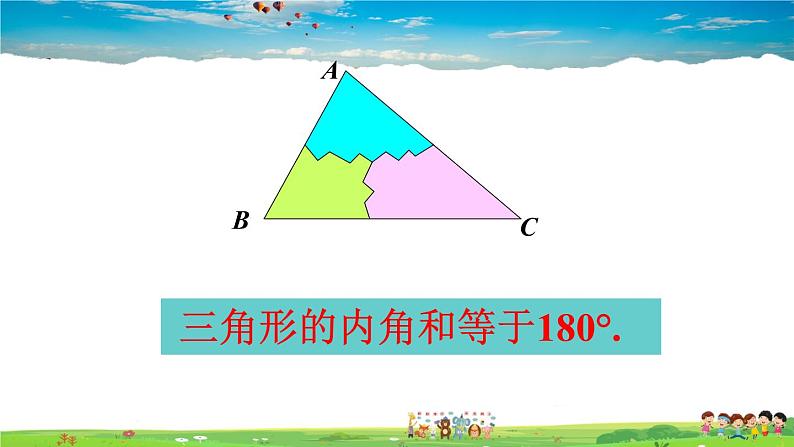
三角形的内角和等于180°.
例2 已知：在△ABC中，BD⊥AC，垂足为D，∠ABD=54°，∠DBC=18°，求∠A和∠C的度数.
解：因为 BD⊥AC，（已知）
所以∠ADB=∠CDB=90°.
在△ABD中，∠A+ ∠ABD+ ∠ADB=180 °， （三角形的内角和等于180°） ∠ABD=54°， ∠ADB=90°，（已知）
∠A=180°-∠ABD-∠ADB=180°-54°-90°=36°.在△ABC中，∠C=180°-∠A-（∠ABD+∠DBC）=180°-36°-（54°+18°）=72°.
1. 在△ABC中：（1）已知：∠A=105°，∠B-∠C= 15°，则∠C= ；（2）已知：∠A：∠B：∠C=3:4:5，则∠C= ；
2. 已知：如图，∠ACB=90°，CD⊥AB，垂足是D.（1）写出图中所有相等的角；（2）写出图中所有直角三角形，并指出它们的斜边.
3. 已知：如图，在△ABC中，AD⊥BC，垂足是D，∠B=70°，∠BAC=46°.求∠CAD的度数.
解：∵AD⊥BC，∴∠BDA=90°，∴∠BAD=180°-90°-70°=20°，又∵∠BAC=46°，∴∠CAD=46°-20°=26°
1. 在△ABC中，∠A=35°，∠ B=43 ° 则∠ C= . 2. 在△ABC中， ∠A :∠B:∠C=2:3:4则∠A = ∠ B= ∠ C= .
3. 如图，某同学把一块三角形的玻璃打碎成三片，现在他要到玻璃店去配一块形状完全一样的玻璃，那么最省事的办法是 ( )
(A)带①去　　　　(B)带②去　　　　(C)带③去　　　　(D)带①和②去
4. 在△ABC中，已知∠A-∠C=25°，∠B-∠A=10°，求∠B的度数.
分析：根据三角形内角和定理可知： ∠A+∠B+∠C=180°，然后结合已知条件便可以求出.
解：在△ABC中， ∠A+∠B+∠C=180°（三角形内角和定理） 联立∠A-∠C=25°，∠B-∠A=10°可得， ∠A=65°，∠B=75°，∠C=40°答：∠B的度数是75°.
三角形内角和定理:三角形的内角和等于180°.
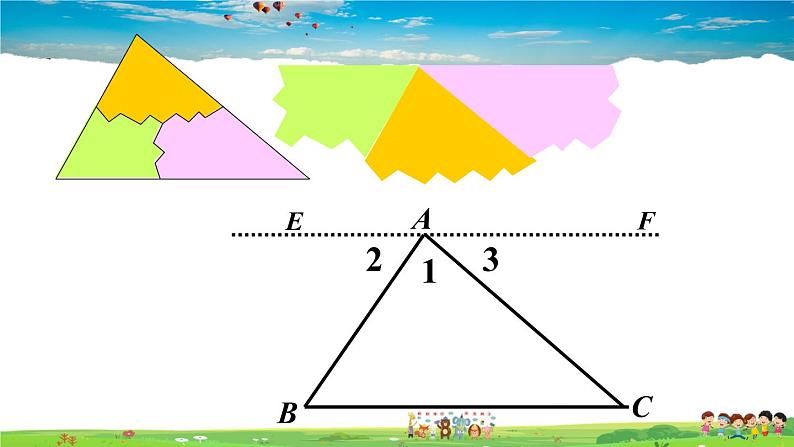
为了说明三个角的和为180°，转化为一个平角，转化思想是数学中的常用方法.